7: Operators, Free Particles and the Quantum Superposition Principle (Lecture)
- Page ID
- 38872
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The equation that substitutes for Newton's equations of motion in classical mechanics (trajectories) is the Schrödinger Equation, which is a wave-equation discussed last week and solutions of which are called wavefunctions. There are two "flavors" of the Schrödinger Equation, the time dependent and the time independent.
\[\hat{H} \psi (x,t) = i \hbar \dfrac{\partial}{\partial t} \psi(x,t) \nonumber\]
The time-dependent Schrödinger Equation results time-dependent wavefunctions with both spatial aspect and a temporal aspects,
\[\hat{H}\psi (x)=E \psi (x) \nonumber\]
The time-independent Schrödinger Equation results in time-independent wavefunctions with only a spatial aspect (the temporal aspects). Which one we use depends on if there is an explicit time-dependence in the Hamiltonian \(\hat{H}\), which is an operator that represents the total energy (e.g., kinetic and potential) of the system. All the topics in Chem 110A, require the use of time-independent Schrödinger Equation, but it is important to recognize that the true wavefunction ALWAYS has a temporal part (we are just ignoring it).
Via the Correspondence Principle, measuring an observable of a quantum system requires solving an eigenvalue problem. Each observable will have a different operator and in general a different set of eigenvalues and eigenvectors. Most of the time (but not always), the observables are quantized and are the eigenvalues of the corresponding operator. For example, to total energy of a quantum system is the eigenvalue of the Hamiltonian operator.
Linearity of Operators
Almost all operators encountered in quantum mechanics are linear operators.
An operator \(\hat{A}\) is linear if
\[ \hat{A}[c_1f_1(x)+c_2f_2(x)]= c_1\hat{A}f_1(x)+c_2\hat{A}f_2(x) \label{linear1}\]
and the operator is nonlinear if
\[\hat{A}[c_1f_1(x)+c_2f_2(x)] \neq c_1\hat{A}f_1(x)+c_2\hat{A}f_2(x)\]
Identifying if an operator is linear is to evaluate the right side and left side of Equation \ref{linear1} independently and ask if they are equal.
Determine from the following operators which are linear and nonlinear:
- \(\hat{A}f(x)= f(x)^2\) [square f(x)]
- \(\hat{A}f(x)= f^*(x)\) [form the complex conjugate of f(x)]
- \(\hat{A}f(x)= 0\) [multiply f(x) by zero]
- \(\hat{A}f(x)= [f(x)]^{-1}\) [take the reciprocal of f(x)]
- \(\hat{A}f(x)= f(0)\) [evaluate f(x) at x=0]
- \(\hat{A}f(x)= \ln f(x)\) [take the log of f(x)]
- Strategy:
-
It is important to note that an operator \(\hat{A}\) is linear if
\[ \underbrace{\hat{A}[c_1f(x)+c_2f_2(x)]}_{\text{left side}}= \underbrace{c_1\hat{A}f_1(x)+c_2\hat{A}f_2(x) }_{\text{right side}}\]
and the operator is nonlinear if
\[ \underbrace{ \hat{A}[c_1f_1(x)+c_2f_2(x)]}_{\text{left side}} \neq \underbrace{ c_1\hat{A}f_1(x)+c_2\hat{A}f_2(x) }_{\text{right side}}\]
- Answer a:
-
Evaluate the left side
\[\begin{align*} \hat{A}[c_1f(x)+c_2f_2(x)] &= [c_1f_1(x)+c_2f_2(x)]^2 \\ &= c_1^2 f_1(x)^2+2c_1f_1(x) c_2f_2(x)+c_2^2f_2(x)^2 \end{align*}\]
Evaluate the right side
\[\begin{align*} c_1 \hat{A} f_1(x)+c_2\hat{A}f_2(x) &=c_1[f_1(x)]^2+c_2[f_2(x)]^2 \\[4pt] &\neq \hat{A}[c_1f_1(x)+c_2f_2(x)] \end{align*}\]
This operator is nonlinear
- Answer b:
-
Evaluate the left side
\[\hat{A}[c_1f_1(x)+c_2f_2(x)] = c_1^*f_1^*(x) + c_2^*f_2^*(x) \nonumber\]
Evaluate the right side
\[\begin{align*} c_1\hat{A}f_1(x) + c_2\hat{A}f_2(x) &= c_1f_1^*(x) + c_2f_2^*(x) \\[4pt] &\neq \hat{A}[c_1f_1(x) + c_2f_2(x)] \end{align*}\]
This operator is not linear (it is formally called antilinear)
- Answer c:
-
Evaluate the left side
\[ \hat{A}[c_1f_1(x)+c_2f_2(x)] = 0\nonumber\]
Evaluate the right side
\[\begin{align*} c_1\hat{A}f_1(x) + c_2\hat{A}f_2(x) &= c_1f_1(x) + c_2f_2(x) = 0 \\[4pt] & = \hat{A}[c_1f_1(x) + c_2f_2(x)] \end{align*}\]
This operator is linear
- Answer d:
-
Evaluate the left side
\[\hat{A}[c_1f_1(x)+c_2f_2(x)] = \dfrac{1}{c_1f_1(x) + c_2f_2(x)}\nonumber\]
Evaluate the right side
\[\begin{align*}c_1\hat{A}f_1(x) + c_2\hat{A}f_2(x) &= \dfrac{c_1}{f_1(x)} + \dfrac{c_2}{f_2(x)} \\[4pt] & \neq \hat{A}[c_1f_1(x) + c_2f_2(x)] \end{align*}\]
This operator is nonlinear
- Answer e:
-
Evaluate the left side
\[\hat{A}[c_1f_1(x)+c_2f_2(x)] = c_1f_1(0) + c_2f_2(0)\nonumber\]
Evaluate the right side
\[ = c_1\hat{A}f_1(x) + c_2\hat{A}f_2(x)\nonumber\]
This operator is linear
- Answer f:
-
Evaluate the left side
\[\hat{A}[c_1f_1(x)+c_2f_2(x)] = \ln [c_1f_1(x) + c_2f_2(x)]\nonumber\]
Evaluate the right side
\[\begin{align*}c_1\hat{A}f_1(x) + c_2\hat{A}f_2(x) &= c1 \ln f_1(x) + c_2 \ln f_2(x) \\[4pt] &\neq \hat{A}[c_1f_1(x) + c_2f_2(x)] \end{align*}\]
This operator is nonlinear
Eigenstates and Eigenvectors and Eigenvalues
Classical mechanic quantities are evaluated by operators in quantum mechanics. A wavefunction fully describes a system via operators. Conceptually, applying operator \(\hat{A}\) to an eigenfunction such as \(\psi (x)\) gives an eigenvalue \(a\) back, multiplied by the same eigenfunction. Mathematically, this looks like
\[\hat{A}\psi (x) = a\psi (x)\]
Applying this concept to the Schrödinger equation is similar. The Schrödinger equation is an eigenvalue problem where the operator in one dimension is
\[\dfrac {-\hbar^2}{2m} \dfrac{d^2}{d x^2}\]
This is commonly referred to as the Hamiltonian with the operator symbol \(\hat{H}\). Rewriting the equation to
\[\hat{H} \psi (x) = E\psi (x)\]
gives a clearer picture - the energy of the wave function is found when applying the Hamiltonian to the wave function.
Often in discussions of quantum mechanics, the terms eigenstate and wavefunction are used interchangeably. The term eigenvalue is used to designate the value of measurable quantity associated with the wavefunction. For example, when discussing the eigenstates of the Hamiltonian (\(\hat{H}\)), the associated eigenvalues represent energies and within the context of the momentum operators, the associated eigenstate refer to the momentum of the particle.
If you took linear algebra, you likely were exposed to the eigenvalue problem in matrix formulation.
\[\begin{bmatrix} A_{11} & A_{12} & \ldots & A_{1n} \\ A_{21} & A_{22} & \ldots & A_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ A_{n1} & A_{n2} & \ldots & A_{nn} \\ \end{bmatrix}\begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix} = \lambda \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix} \]
Commonly Used Operators
Although we could theoretically come up with an infinite number of operators, in practice there are a few which are much more important than any others.
- Linear Momentum:
The linear momentum operator of a particle moving in one dimension (the \(x\)-direction) is
\[\hat p_x = -i \hbar \dfrac{\partial}{\partial x} \label{3.3.7}\]
and can be generalized in three dimensions:
- Kinetic Energy
Classically, the kinetic energy of a particle moving in one dimension (the \(x\)-direction), in terms of momentum, is
\[KE_{classical}= \dfrac{p_x^2}{2m} \label{3.3.9}\]
Quantum mechanically, the corresponding kinetic energy operator is
\[ \hat {KE}_{quantum}= -\dfrac{\hbar^2}{2m} \dfrac{\partial^2}{\partial x^2}\label{3.3.10}\]
and can be generalized in three dimensions:
\[ \hat {KE}_{quantum}= -\dfrac{\hbar^2}{2m} \nabla^2 \label{3.3.11}\]
- Angular Momentum:
Angular momentum requires a more complex discussion, but is the cross product of the position operator \(\hat{\vec{r}}\) and the momentum operator \(\hat p\)
\[ \hat {\vec{L}} = -i \hbar ( \vec{r} \times \nabla) \label{3.3.12}\]
- Hamiltonian:
The Hamiltonian operator corresponds to the total energy of the system
and it represents the total energy of the particle of mass \(m\) in the potential \(V(x)\). The Hamiltonian in three dimensions is
\[\hat{H}=-\dfrac{\hbar^2}{2m}\nabla^2+V(\vec{r}) \label{3.3.5a}\]
- Energy:
The energy operator from the time-dependent Schrödinger equation
The right hand side of Equation \(\ref{3.3.14}\) is the Hamiltonian Operator.
Wavefunctions Have a Probabilistic Interpretation
The Born interpretation calls the wavefunction squared the probability density, and the probability density times a volume element in three-dimensional space (\(d\tau\)) is the probability \(P\) (i.e., a number between 0 and 1)
\[ P(\vec{r},t)= \Psi^*(r,t) \Psi(r,t) = {|\Psi(r,t)|}^2 \]
The probability that a single quantum particle moving in one spatial dimension will be found in a region between \(a\) and \(b\) (i.e, \(x\in[a,b]\)) if a measurement of its location is performed is
\[P(x\in[a,b])=\int_{a}^{b}|\psi (x)|^2 dx \label{3.4.2}\]
In three dimensions, Equation \(\ref{3.4.2}\) is represented differently
\[P(x \in[a_1\,a_2\,a_3,b_1\,b_2\,b_3])=\int_{a_1}^{b_1}\int_{a_2}^{b_2}\int_{a_3}^{b_3}|\psi (\vec{\tau})|^2 d\tau \label{3.4.3}\]
where \(d\tau\) is the infinitesimal volume element (changes based on coordinate system used). Equation \ref{3.4.3} is the probability that a single quantum particle moving in three spatial dimensions will be found in a region between \(a_1\) and \(b_1\) (i.e, \(x \in [a_1,b_b]\)), \(a_2\) and \(b_2\) (i.e, \(y\in[a_1,b_b]\)), and \(z_3\) and \(b_3\) (i.e, \(z\in[a_1,b_b]\)); this presume we are using Cartesian coordinates to describe space (i.e., \(x\), \(y\) and \(x)\)).
The Quantum Mechanical Free Particle
The simplest system in quantum mechanics has the potential energy \(V=0\) everywhere. This is called a free particle since it has no forces acting on it. We consider the one-dimensional case, with motion only in the \(x\)-direction, giving the time-independent Schrödinger equation
\[- \dfrac{\hbar^{2}}{2m}\dfrac{d^{2}\psi (x)}{dx^2}= E\psi (x)\label{1}\]
or more simply
\[ \hat{H} \psi (x)= E\psi (x)\label{H1}\]
with
\[ \hat{H} = - \dfrac{\hbar^{2}}{2m}\dfrac{d^{2} }{dx^2} \label{H2}\]
Total derivatives can be used since there is one independent variable. The Schrödinger equation simplifies to
\[\psi'' (x)+k^{2}\psi (x)=0\label{2}\]
with the definition
\[k^2 \equiv \dfrac{2mE}{\hbar^2}\label{3}\]
Possible solutions of Equation \ref{2} are
\[\psi (x)= const\begin{Bmatrix}
\sin(kx)\\
\cos(kx)\\
e^{\pm ikx}\end{Bmatrix}\label{4}\]
There is no restriction on the value of \(k\). Thus a free particle, even in quantum mechanics, can have any non-negative value of the energy
\[E=\dfrac{\hbar^2k^2}{2m}\geq 0\label{5}\]
The energy levels in this case are not quantized and correspond to the same continuum of kinetic energy shown by a classical particle.
Consider for a free particle (i.e., \(V(x)=0\)) moving in one dimension.
- Demonstrate that \(\sin (kx)\) is an eigenfunction of \(\hat{H}\).
- What are their corresponding eigenstates?
- Why are the energies not quantized?
- Approach
-
To demonstrate that a function is indeed a specific eigenfunction \(f(x)\) of an operator \(\hat{O}\), we have to ask if this Eigenvalue equation is correct, i.e., \[ \hat{O} f(x) = \lambda f(x) \label{Eigen1}\] where \(\lambda\) is the eigenvalue associated with that eigenfunction associated with the operator. Change the operator and the eigenfunctions and eigenvalues will change. Change the eigenfunction and the eigenvalue will change. They are all connected like the Mufasa's "Circle of Life."
- Solution A
-
Let's take the \(\sin (kx)\) function and the Hamiltonian operator (Equation \ref{H2}) and insert it into Equation \ref{Eigen1} and is if the equality is ensured. Keep in mind that any value of \(lambda\) will work as long as it is a constant.
\[ - \dfrac{\hbar^{2}}{2m}\dfrac{d^{2}}{dx^2} \sin (kx) \overset{?}{=} \lambda \sin (kx) \label{Eigen1A}\]
first step in evaluating the 2nd derivative
\[ - \dfrac{\hbar^{2}}{2m} k \dfrac{d }{dx} (\cos (kx)) \overset{?}{=} \lambda \sin (kx) \label{Eigen1B}\]
and second step
\[ + \dfrac{\hbar^{2}}{2m} k^2 (\sin (kx)) \overset{?}{=} \lambda \sin (kx) \label{Eigen1C}\]
This equation is confirmed when
\[\lambda = + \dfrac{\hbar^{2} k^2}{2m} \]
Which makes sense when compared to Equation \ref{5} since the Hamiltonian gives the total energy \(E\).
- Solution B
-
As shown in the Solution A, the Eigenvalue equation is confirm to be correct for all \(\sin (kx)\) functions (so they are eigenfunctions of the Hamiltonian) and the eigenvalues are \[\lambda = + \dfrac{\hbar^{2} k^2}{2m} .\] Eigenvalues can be positive, negative, real, imaginary and complex and all of the above.
- Solution C
-
Since any value of \(k\) is allowed in the \(\sin (kx)\) eigenfunctions (i.e., the Eigenvalue equation holds for all values of \(k\)), then there is no quantization. We need boundary conditions to force the quantization like with the Bohr hydrogen atom.
A free particle, even in quantum mechanics, can have any non-negative value of the energy. Its energy is NOT quantized.
It is of interest also to consider the x-component of linear momentum for the free-particle solutions (Equation \ref{4}). The eigenvalue equation for momentum is
\[\hat{p}_{x}\psi (x)=-i\hbar\dfrac{d\psi (x)}{dx}=p\psi (x)\label{6}\]
where we have denoted the momentum eigenvalue as \(p\).
Below is a circle in the complex plane with a blue line drawn from the center to the circle, a bit like a spoke on a wheel.
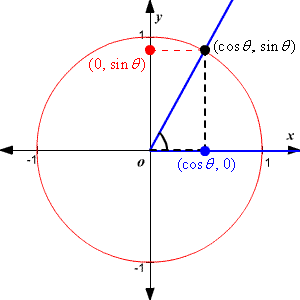
It’s a line with a direction (out from the center) so it’s a vector, which is excellent because you’ve already decided you’re going to be using vectors and linear algebra.
Real part oscillates in time (left) and imaginary part oscillates in time (but out of phase with real).
The vectors are imaginary things that live in the complex plane, so you understand their linear sum will just express the probability of a photon being there. The square of the length of the new arrow represents the probability of finding a photon at that location.
So the pictures of the spokes moving are just animated pictures of the first red circle, and the plane the spokes are moving in is the complex plane. You can use Euler’s famous formula to describe them. Euler’s formula is
\[e^{i \theta}=\cos \theta+i \sin \theta\]
Replace theta with \(t\) for time, and plot the function on the complex plane.
This is a picture of doing that and stretching the time axis out.
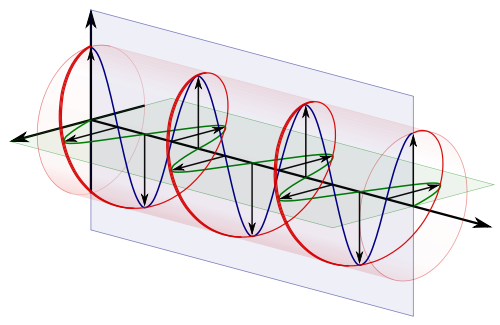
So this is the same picture of the complex plane, with our spinning spokes on it, moving through time, a bit like this :
The arrow traces out the red spiral which looks like a wave.
Another way to look the wavefunction for a free particle
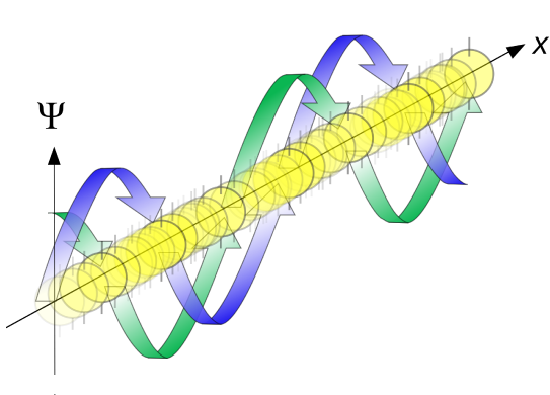
Back to the Superposition Principle
The functions \(\sin kx\) and \(\cos kx\) are not eigenfunctions of \(\hat{p}_{x}\), but are each superpositions of the two eigenfunctions \(e^{\pm ikx}\), by virtue of the trigonometric identities
\[\cos (kx)=\dfrac{1}{2}(e^{ikx} +e^{-ikx})\]
and
\[\sin(kx)= \dfrac{1}{2i}(e^{ikx} -e^{-ikx})\label{7}\]
The eigenfunction \(e^{ikx}\) for \( k > 0\) represents the particle moving from left to right on the x-axis (blue curve in Figure \(\PageIndex{2}\)) with momentum \(p > 0\). Correspondingly, \(e^{-ikx}\) represents motion from right to left with \(p < 0\) (red curve in Figure \(\PageIndex{2}\)).
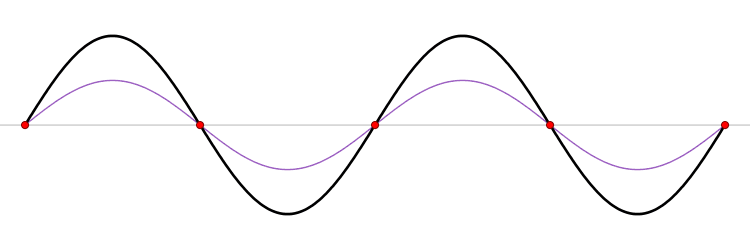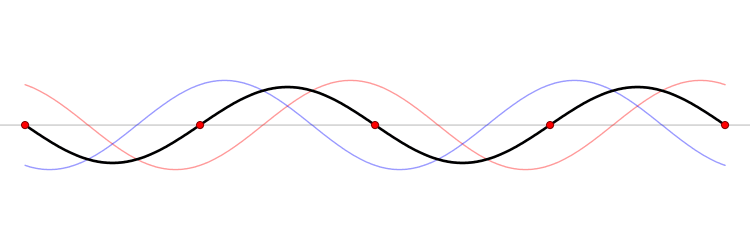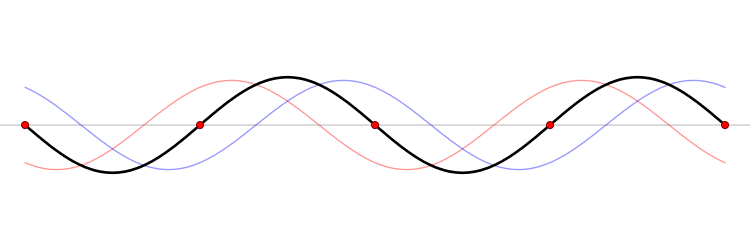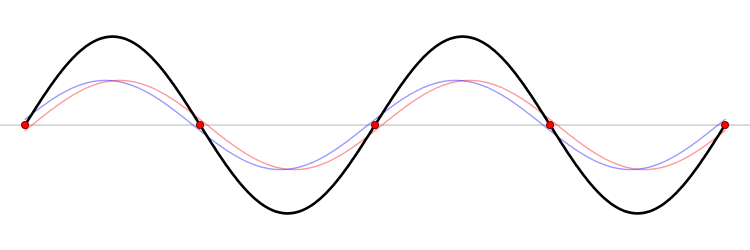
Wavepackets - The Superposition Principle in Action
If we add together two sine waves with frequencies close together, we get "beats." This pattern can be viewed as a string of wavepackets. For example, consider adding two sine waves together with spatial and temporal frequencies of \((k \pm \Delta k\)) and (\( \omega \pm \Delta \omega\)), respectively.
\[\sin \left[(k - \Delta k) x - (\omega - \Delta \omega) t \right] + \sin \left[ (k + \Delta k) x - ( \omega + \Delta \omega )t \right]) \label{WP1}\]
If we use the trigonometric addition formula, the sum in Equation \ref{WP1} can be simplified to
\[ 2 \sin (kx - \omega t ) \cos \left[ (\Delta k) x - (\Delta \omega)t \right] \label{beats}\]
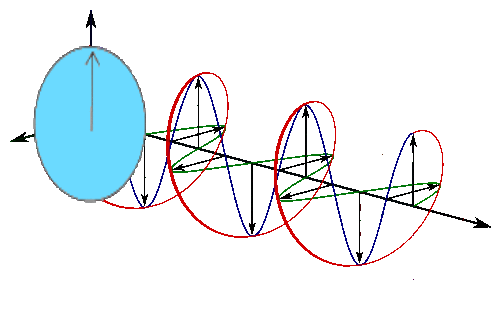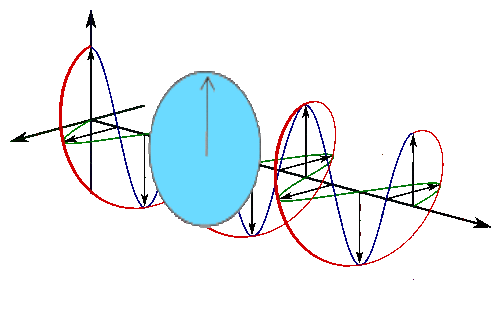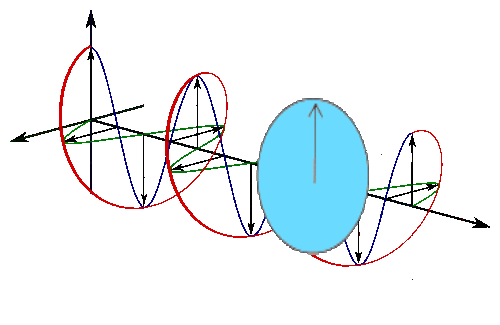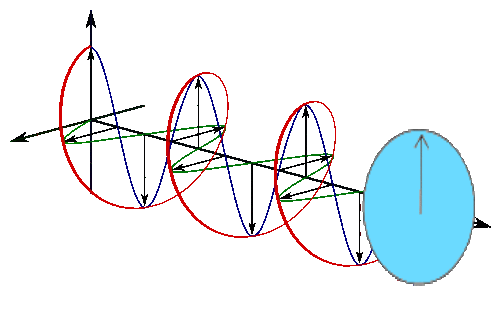
Sine waves extend to infinity in both spatial directions, so they cannot represent a particle whose wavefunction is nonzero in a limited region of space. Physically, that it must have a wavefunction that goes to zero far away in either direction. A localized wavefunction of this type is called a “wavepacket”. A wavepacket can be constructed by adding plane waves together.
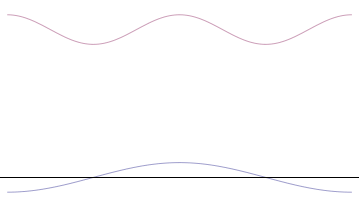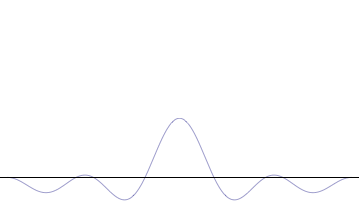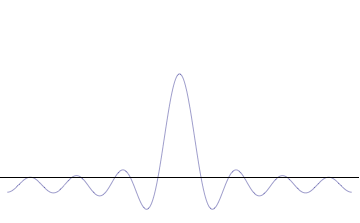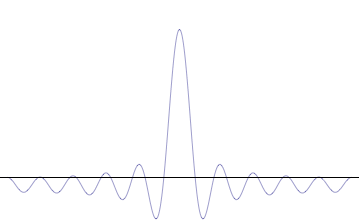
This wavepacket perspective of a free particle is shown in Figure \(\PageIndex{4}\), where the wavefunction amplitude (both real and imaginary) is localized and tapers off on either side (contrast this image with Figure \(\PageIndex{1}\) that exhibits uniform amplitude over all space since it is a oscillatory eigenfunction.
\[\Psi=\sum_{n} A_{n} e^{i\left(p_{n} x-\omega_{n} t\right)}\]
- The appropriate Hamiltonian (\(\hat{H}\)) for the system
- The specific functional form for the solutions of the Eigenvalue problem with this operator.
- The specific functional form of the eigenvalues associated with the eigenfunctions (i. e., solutions)
- Identify the relevant quantum number(s) for the solution
- Identify the relevant range of the quantum numbers.
Once you get these basics down, then you can start to do some fun quantuming.


https://movieblow.wordpress.com/