Homework 4 (Larsen)

Name: ______________________________

Section: _____________________________

Student ID#:__________________________

Q-3

What is the expectation value of kinetic energy for a particle in a box of length (\(L\)) in the ground eigenstate (n=1)? What about for the first excited eigenstate (n=2). Explain the difference.

Q-2

What is the most probable position for a particle in a box of length (\(L\)) in the ground eigenstate (n=1)? What about for the first excited eignestate (n=2). Explain the difference.

Q-1

Find the following expectation values for a particle with mass, \(m \), in a 3D box with dimensions \(a_1 \), \(a_2 \), \(a_3 \). Assume that the quantum numbers are given by \(n_x\), \(n_y\), and \(n_z\).

1. \( \langle x \rangle \)
2. \( \langle y \rangle \)
3. \( \langle z \rangle \)
4. \( \langle p_z \rangle \)
5. \( \langle z^2 \rangle \)
6. \( \langle z \rangle^2 \)

Q0

Consider a particle of mass \(m\) in a two-dimensional square box with sides \(L\). Calculate the four lowest (different!) energies of the system. Write them down in the increasing order with their principal quantum numbers.

Q1

The 2D particle in a box model can be used to describe the spectra of aromatic hydrocarbons. Assume a rectangular box that extends one bond length beyond the carbon atoms to contain the hydrogen atoms in the box. Hint: You will have to use some trigonometry basics to get the relevant dimensions.

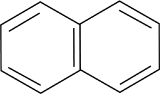
a. Calculate the first three electronic transitions for napthalene (bond length 1.42 Angstroms).

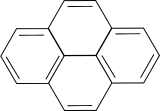
b. Calculate the first three electronic transitions for pyrene (bond length 1.42 Angstroms).

Q2

For a quantum wire made from Silicon Telluride (Si₂Te₃) with a length of 17 nm (assuming the other dimensions have 0 units), what is the energy required (in electron volts) to make a transition from the state n=1 to n=2? The measured value for this transition is about 1.9 eV (652.5nm). What would the mass of the electron be if this were the energy measured?

Quantum Wire. Nanostructural size heterostructure diagram that gives rise to quantum effects. (CC BY-SA 3.0; Gianderiu).

Q3

Find the normalization constant \(A\) in the following wavefunctions:

\[ \psi(x) = Ae^{ikx}\]

\[ \psi(x) = Ae^{-ikx}e^{-x^2/2a^2}\]

Q4

Find the normalization constant for the wavefunction:

\[
\psi(x)=\left\{
\begin{array}{ll}
C \quad \frac{-c}{4} \leq x \leq \frac{c}{4} \\
0 \qquad \textrm{elsewhere} \\
\end{array}
\right.
\]

Q5

Show that the eigenstates to a particle in a 1D box with infinite potential satisfy the orthogonormality relationship:

\[ \int_{-\infty}^{\infty} \psi_n^*(x) \psi_m(x)\; dx = 1 \; \text{if } m=n\]

and

\[ \int_{-\infty}^{\infty} \psi_n^*(x) \psi_m(x)\; dx = 0 \; \text{if } m \neq n\]

What is the origin of the first equation?

Q6

A particle of mass \(m\) moves in a one-dimensional box of length \(L\) with boundaries at \(x = 0\) and \(x = L\).

• For any generic wavefunction \(\psi_n(x)\) for this system, calculate the probability that the particle is found somewhere in the region 0 ≤ x ≤ L/8.
• Show how this probability depends on \(n\).
• For what value of n is there the largest probability of finding the particle in 0 ≤ x ≤ L/8?

Q7

Evaluate the following commutators \( [\hat{A}, \hat{B}] \) for the following pair of operators:

1. \(\hat{C}\) and \([\hat{D},\hat{C}]\hat{E} \)
2. \(\dfrac{d}{dz}\) and \(z \)
3. \(\dfrac{d^2}{dz^2}\) and \( z \)
4. \(\dfrac{d^2}{dz^2}\) and \( z^2 \)
5. \( \dfrac{d^2}{dy^2}\) and \(y \)
6. \(\dfrac{d}{dz}-z\) and \(\dfrac{d}{dz}+z \)
7. \(\dfrac{d}{dz}\) and \(\displaystyle \int_{0}^{z} dz \)
8. \(\dfrac{1}{2}\) and \(\dfrac{d}{dy} \)
9. \( x^2 - \dfrac{d^2}{dx^2} \) and \( x - \dfrac{d}{dx} \)
10. \( \hat{p}_z = -i \hbar \dfrac{\partial}{\partial z} \) and \( \hat{L}_z = -i \hbar \left( x \dfrac{\partial}{\partial y} - y \dfrac{\partial}{\partial x} \right) \)

Q8

For the following molecules identify the number of

• degrees of freedom,
• translational degrees of freedom
• rotational degrees of freedom
• vibrational degrees of freedom
  

1. \(Ne\)
2. \(C_{60}\)
3. \(N_2\)
4. HCN
5. \(CO_2\)
6. \(UF_6\)

Q9

The wavefunctions for the quantum mechanical harmonic oscillator \(| \psi_v \rangle\) in atomic units with \(\alpha = 1 \) are expressed as

\[ | \psi_v \rangle = N_v H_v e^{-(x-x_o)^2/2} \]

with

• \(x_o\) is the equilibrium position of the oscillator
• \(N_v\) is a normalization factor for a specific \(v\) value
• \(H_v\) is the Hermite polynomial for a specific \(v\) value (see Table M1)

What is the wavefunction (with determined normalization factor) for the harmonic oscillator in the \(v=0\) state?

Q10

Calculate the expectation value of \( x \) of the quantum harmonic oscillator \(x\) from equilibrium when the oscillator is in the \(v=0\) and \(v=1\) quantum states.

Q11

Calculate the expectation value of \(x^2 \) (i.e., \(\langle x^2 \rangle\)) of the quantum harmonic oscillator \(x\) from equilibrium when the oscillator is in the \(v=0\) and in the \(v=1\) quantum states.

Q12

Use the answers from Q9 and Q10 to determined the uncertainty of position of a particle following the harmonic oscillator with \(v=0\)?

Q13

A particle with an effective mass of \(1 \times 10^{-28} \;kg\) oscillates in a well according to the quantum harmonic oscillator, the energy levels are separated by \(2.5 \times 10^{-24}\; J\). What is the force constant for the oscillator? What is the zero point energy of this oscillator?