Homework 4 Key (Koski)

Q1

The 2D particle in a box model can be used to describe the spectra of aromatic hydrocarbons. Assume a rectangular box that extends one bond length beyond the carbon atoms to contain the hydrogen atoms in the box. Hint: You will have to use some trigonometry basics to get the relevant dimensions.

a. Calculate the first three electronic transitions for napthalene (bond length 1.42 Angstroms).

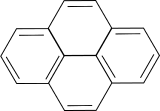
b. Calculate the first three electronic transitions for pyrene (bond length 1.42 Angstroms).

Solution 1:

The energies of an electron of mass \(m\) in a two-dimensional square box with sides \(L\) are:

\(E_{n_x,n_y}=\dfrac{h^{2}}{8m}(\dfrac{n_x^{2}}{L_x^{2}}+\dfrac{n_y^{2}}{L_y^{2}})\), \(n_x,n_y=1,2,...\).

a.

The first step is to find \(L_x\) and \(L_y\). In order to do this, we must first choose the correct orientation of the molecule - this may not be immediately obvious to students, so perhaps we should accept either of two logical choices: setting \(L_x\) and \(L_y\) along the horizontal and vertical axes, or rotated 30 degrees (which is correct).

Recall trigonometric identities for a unit hexagon:

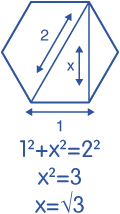
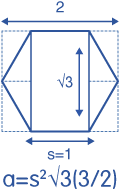https://hexnet.org/content/hexagonal-geometry

If we were to rotate the molecule by 30 degrees, the lengths that we calculate would be:

\(L_x = 4 \times 1.42\) Angstroms \(= 5.6 \) Angstroms

\(L_y = 6 \cos 30 \times 1.42\) Angstroms \(= 7.27\) Angstroms

This gives:

\(E_{n_x,n_y} = a(n_x^2 + 0.593 n_y^2)\) if we let \(a = \dfrac{h^2}{8m}\) and divide through by \(L_x^2\).

First few energy levels:
\(n_x\) \(n_y\) E

1. 1 1 1.593 a
2. 1 2 3.373 a
3. 2 1 4.593 a
4. 1 3 6.340 a
5. 2 2 6.373 a
6. 2 3 9.340 a
7. 2 4 13.488 a
8. 3 3 14.337 a

Napthalene has 5 double bonds, thus 10 \(\pi\) electrons. The first five levels are doubly occupied so the first three transitions are:

\(\Delta E_1 = E_{23} - E_{22} = 2.967a (~2.87 \times 10^4 cm^{-1} )\)

\(\Delta E_2 = E_{23} - E_{13} = 3.000a (~2.90 \times 10^4 cm^{-1} )\)

\(\Delta E_3 = E_{24} - E_{22} = 7.115a\)

b.

We again encounter a question as to the orientation of the molecule in order to find \(L_x\) and \(L_y\).

If we were to rotate the molecule by 30 degrees, the lengths that we calculate would be:

\(L_x = 4 \times 1.42\) Angstroms \(= 5.6 \) Angstroms

\(L_y = 12 \cos 30 \times 1.42\) Angstroms \(= 14.54\) Angstroms

This gives:

\(E_{n_x,n_y} = a(n_x^2 + 0.148 n_y^2)\) if we let \(a = \dfrac{h^2}{8m}\) and divide through by \(L_x^2\).

First few energy levels:
\(n_x\) \(n_y\) E

1. 1 1 1.148 a
2. 1 2 1.592 a
3. 1 3 2.332 a
4. 2 1 4.148 a
5. 2 2 4.592 a
6. 2 3 5.332 a
7. 2 4 6.368 a
8. 3 1 9.148 a
9. 3 3 10.332 a
10. 3 4 11.368 a

Pyrene has 8 double bonds, thus 16 \(\pi\) electrons. The first eight levels are doubly occupied so the first three transitions are:

\(\Delta E_1 = E_{33} - E_{31} = 1.184a\)

\(\Delta E_2 = E_{34} - E_{31} = 2.220a\)

\(\Delta E_3 = E_{33} - E_{24} = 3.964a\)

*Note that coefficients may vary since \(a=\dfrac{h^{2}}{8m}=\dfrac{(2\pi\hbar)^{2}}{8m}=\dfrac{4\pi^{2}\hbar^{2}}{8m}=\dfrac{\pi^{2}\hbar^{2}}{2m}\).

Q2

For a quantum wire made from Silicon Telluride (Si₂Te₃) with a width of 17 nm, what is the energy required (in electron volts) to make a transition from the state n=1 to n=2? The measured value for this transition is about 1.9 eV (652.5nm). What would the mass of the electron be if this were the energy measured?

Quantum Wire. Nanostructural size heterostructure diagram that gives rise to quantum effects. (CC BY-SA 3.0; Gianderiu).

Solution 2:

We can apply the 1D particle in a box model here to approximate the energy required for this transition. The general formula for the energy of transitions between neighboring states is:

\(E_{n+1}- E_n= \dfrac{(n+1)^{2}h^{2}}{8mL^{2}}-\dfrac{n^{2}h^{2}}{8mL^{2}}=\dfrac{(n^2+2n+1)h^{2}}{8mL^{2}}-\dfrac{n^{2}h^{2}}{8mL^{2}}=\dfrac{(2n+1)h^{2}}{8mL^{2}}, n=1,2,.... \tag{21}\)

Therefore, using a box length of \(1.7 \times 10^-8\)m and the mass of an electron, the energy that is needed for a transition from the \(n=1\) to \(n=2\) state is:

\(\Delta E_{12} = \dfrac{(2^2-1^2) h^2}{8m_e L^2} = 3.9\) meV

However, the difference between this value and the actual value of 1.9 eV comes about from the fact that, in reality, we need to use a reduced mass. To find what this mass is, we can rearrange the energy expression and solve for m, substituting 1.9 eV for the transition energy:

\( \mu = \dfrac{3 h^2}{8L^2 (1.9 eV)(1.6 \times 10^{-19} J/ev)} = 1.87\times 10^{-33}\) kg

Q3

Find the normalization constant \(A\) in the following wavefunctions:

\[ \psi(x) = Ae^{ikx}\]

\[ \psi(x) = Ae^{-ikx}e^{-x^2/2a^2}\]

Solution 3:

Plane wave solutions to the Schrödinger equation (i.e., for a free particle) are not normalizable because they extend to infinity with a constant amplitude. This is the case for the first wavefunction. However, any physical particle will be constrained to a finite space (at least to the visible universe), so we need to look at superpositions of plane waves. This means that our starting point is:

\(\psi(x,0)=\int_{-\infty}^{\infty} dk\psi'(k)e^{-ikx} \psi(x,0)=\int_{-\infty}^{\infty} dk\psi'(k)e^{-ikx}\).

where \(\psi(k)\) is some function with a finite width. In this case, then, we can "normalize" to the Dirac delta function, rather than 1, by taking ψ̃ (k)=δ(k−k′)ψ(k)=δ(k−k′).

For the second wavefunction, we use the normalization condition: \(\int_{-\infty}^{\infty} \psi^*(x) \psi(x)dx=1\). To calculate this integral we need \(\psi^*(x)\) which we find by taking complex conjugate of \(\psi(x)\). Taking complex conjugate of \(\psi(x)\) in this case is simply reversing the sign before \(i\) : \( \psi^*(x) = Ae^{-ikx}e^{-x^2/2a^2}\). Further we plug \(\psi(x)\) and \(\psi^*(x)\) in the normalization condition:

\[ \int_{-\infty}^{\infty} \psi^*(x) \psi(x)dx=\int_{-\infty}^{\infty} Ae^{-ikx}e^{-x^2/2a^2}Ae^{ikx}e^{-x^2/2a^2}dx=\int_{-\infty}^{\infty} A^{2}e^{-x^2/2a^2}e^{-x^2/2a^2}dx=\\ \int_{-\infty}^{\infty} A^{2}e^{-2x^2/2a^2}dx=\int_{-\infty}^{\infty} A^{2}e^{-x^2/a^2}dx= a/a \int_{-\infty}^{\infty} A^{2}e^{-(x/a)^2} dx=\\ a \int_{-\infty}^{\infty} A^{2}e^{-(x/a)^2}(\dfrac{1}{a})dx = a \int_{-\infty}^{\infty} A^{2}e^{-(x/a)^2}d(\dfrac{x}{a})=\text (substitution \ of \ variables)=A^{2}a\sqrt{\pi}=1\]

\[A=\pm\sqrt{1/(a\sqrt{\pi})}\]

Q4

Find the normalization constant for the wavefunction:

\[
\psi(x)=\left\{
\begin{array}{ll}
C \quad \frac{-c}{4} \leq x \leq \frac{c}{4} \\
0 \qquad \textrm{elsewhere} \\
\end{array}
\right.
\]

Solution 4:

Assume the normalization constant is A. Use the normalization condition:

\[\int_{-\infty}^{\infty} A\Psi ^{*} (x) A\Psi (x) dx = 1\]

\[1= \int_{-\infty}^{\infty} A\Psi ^{*} (x) A\Psi (x) dx = A^2\int_{-\infty}^{\infty}\Psi^* \Psi(x) dx=A^2 \int_{-\infty}^{-\dfrac{C}{4}} 0\times0 dx +A^2 \int_{\dfrac{C}{4}}^{\infty} 0\times0 dx +A^2 \int_{-\dfrac{C}{4}}^{\dfrac{C}{4}} C^2 dx=0+0+A^2 C^2 \dfrac{C}{2}=1\]

So \(A=\pm \sqrt{\dfrac{2}{C^3}}\)

Q5

Show that the eigenstates to a particle in a 1D box with infinite potential satisfy the orthogonormality relationship:

\[ \int_{-\infty}^{\infty} \psi_n^*(x) \psi_m(x)\; dx = 1 \; \text{if } m=n\]

and

\[ \int_{-\infty}^{\infty} \psi_n^*(x) \psi_m(x)\; dx = 0 \; \text{if } m \neq n\]

What is the origin of the first equation?

Solution 5:

Eigenstates of a particle in 1D box of length \(L\) is given by the expression \(\psi_n = \sqrt{\dfrac{2}{L}}\sin{\dfrac{n\pi x}{L}}, n=1,2,...\). To show that these eigenstates satisfy \((1)\) we need to plug \(\psi_n\) with the same principal quantum number \(n\) (or subscript) in expression \((1)\):

\[ \int_{0}^{L} \psi_n^*(x) \psi_n(x) dx =\int_{0}^{L} \dfrac{2}{L}\sin^2{\dfrac{n\pi x}{L}}dx=\dfrac{2}{L}\dfrac{1}{2}\int_{0}^{L}(1-cos{\dfrac{2n\pi x}{L}})dx=\\ \dfrac{1}{L}x\Biggr\rvert_{0}^{L} +\dfrac{1}{L}\dfrac{L}{2n\pi}(-\sin{\dfrac{2n\pi x}{L}})\Biggr\rvert_{0}^{L}=\dfrac{1}{L}L-\dfrac{1}{L}0-\sin{\dfrac{2n\pi L}{L}}+\sin{(0)}=1-0-0+0=1\]

This is correct according to Postulate 2 (normalization condition).

To show that the eigenstates satisfy \((2)\) we need to plug \(\psi_n\) and \(\psi_m\) with different principal quantum numbers \(n\) and \(m\) (or subscripts) in expression \((2)\):

\[ \int_{-\infty}^{\infty} \psi_n^*(x) \psi_m(x) dx =\int_{0}^{L} \dfrac{2}{L}\sin{\dfrac{m\pi x}{L}}\sin{\dfrac{n\pi x}{L}}dx=\dfrac{2}{L}\dfrac{1}{2}\int_{0}^{L}\cos{(\dfrac{m\pi x}{L}-\dfrac{n\pi x}{L})}-\cos{(\dfrac{m\pi x}{L}+\dfrac{n\pi x}{L})}dx= \\ \dfrac{1}{L}\int_{0}^{L}\cos{\dfrac{(m-n)\pi x}{L}}+\cos{\dfrac{(m+n)\pi x}{L}}dx=\dfrac{1}{L}(\dfrac{L}{(m-n)\pi}\sin{\dfrac{(m-n)\pi x}{L}}+\dfrac{L}{(m+n)\pi}\sin{\dfrac{(m+n)\pi x}{L}})\Biggr\rvert_{0}^{L}=\\ \dfrac{1}{L}(\dfrac{L}{(m-n)\pi}\sin{\dfrac{(m-n)\pi L}{L}}-0+\dfrac{L}{(m+n)\pi}\sin{\dfrac{(m+n)\pi L}{L}}-0)=\\ \dfrac{1}{L}(\dfrac{L}{(m-n)\pi}\sin{((m-n)\pi)}-0+\dfrac{L}{(m+n)\pi}\sin{((m+n)\pi)}-0) =\dfrac{1}{L}(0-0+0-0)=0\]

The origin of the first equation is the same as the origin of the normalization condition. By stating \((1)\) or normalization condition we mean that the object that we are describing with the wavefunctions \({\psi_n(x)}\) exists.

Q6

A particle of mass \(m\) moves in a one-dimensional box of length \(L\) with boundaries at \(x = 0\) and \(x = L/2\) .

• For any generic wavefunction \(\psi_n(x)\) for this system, calculate the probability that the particle is found somewhere in the region 0 ≤ x ≤ L/8.
• Show how this probability depends on \(n\).
• For what value of n is there the largest probability of finding the particle in 0 ≤ x ≤ L/8?

Solution 6:

\[ P(0 ≤ x ≤ L/8)=\int_{0}^{L/8} \psi^*(x) \psi(x)dx=\int_{0}^{L/8}\dfrac{2}{L}\sin^2{\dfrac{n\pi x}{L}}dx=\dfrac{2}{L}\dfrac{1}{2}\int_{0}^{L/8}(1-\cos{\dfrac{2n\pi x}{L}})dx=\\ \dfrac{1}{L}x\Biggr\rvert_{0}^{L/8} +\dfrac{1}{L}\dfrac{L}{2n\pi}(-\sin{\dfrac{2n\pi x}{L}})\Biggr\rvert_{0}^{L/8}=\dfrac{1}{L}\dfrac{L}{8}-\dfrac{1}{L}0-\dfrac{1}{2n\pi}\sin{\dfrac{2n\pi L}{8L}}+\dfrac{1}{2n\pi}\sin{(0)}=\\ \dfrac{1}{8}-0-\dfrac{1}{2n\pi}\sin{\dfrac{n\pi}{4}}+0=\dfrac{1}{8}-\dfrac{1}{2n\pi}\sin{\dfrac{n\pi}{4}}\]

\(\dfrac{1}{8}-\dfrac{1}{2n\pi}\sin{\dfrac{n\pi}{4}}\) is the largest when \(\dfrac{1}{2n\pi}\sin{\dfrac{n\pi}{4}}\) is the smallest. Since the latter is the product of the oscillating \(\sin{\dfrac{n\pi}{4}}\) and decreasing \(\dfrac{1}{2n\pi}\) function we can say that there is no smallest value of \(\dfrac{1}{2n\pi}\sin{\dfrac{n\pi}{4}}\). However, when \(n\) is getting larger \(\dfrac{1}{2n\pi}\sin{\dfrac{n\pi}{4}}\) is getting smaller (see figure below). We can also simply find the smallest n for which sine will be -1 so we can add \(\dfrac{1}{2n\pi}\) to 1/8. This corresponds to n = 6. However, the sine term is also minimized as n goes to \(\infty\).

Q7

Evaluate the following commutators \( [\hat{A}, \hat{B}] \) for the following pair of operators:

1. \(\hat{C}\) and \([\hat{D},\hat{C}]\hat{E} \)
2. \(\dfrac{d}{dz}\) and \(z \)
3. \(\dfrac{d^2}{dz^2}\) and \( z \)
4. \(\dfrac{d^2}{dz^2}\) and \( z^2 \)
5. \( \dfrac{d^2}{dy^2}\) and \(y \)
6. \(\dfrac{d}{dz}-z\) and \(\dfrac{d}{dz}+z \)
7. \(\dfrac{d}{dz}\) and \(\displaystyle \int_{0}^{z} dz \)
8. \(\dfrac{1}{2}\) and \(\dfrac{d}{dy} \)
9. \( x^2 - \dfrac{d^2}{dx^2} \) and \( x - \dfrac{d}{dx} \)
10. \( \hat{p}_z = -i \hbar \dfrac{\partial}{\partial z} \) and \( \hat{L}_z = -i \hbar \left( x \dfrac{\partial}{\partial y} - y \dfrac{\partial}{\partial x} \right) \)

Solution 7:

a. \(\hat{C}\) and \([\hat{D},\hat{C}]\hat{E} \)

\(\hat{A} =\hat{C}\) ; \(\hat{B}=[\hat{D},\hat{C}]\hat{E}\)

\[[\hat{A},\hat{B}]=\hat{A}\hat{B}-\hat{B}\hat{A}=\hat{C}[\hat{D},\hat{C}]\hat{E}-[\hat{D},\hat{C}]\hat{E}\hat{C}=\hat{C}(\hat{D}\hat{C}-\hat{C}\hat{D})\hat{E}-(\hat{D}\hat{C}-\hat{C}\hat{D})\hat{E}\hat{C}=\hat{C}\hat{D}\hat{C}\hat{E}-\hat{C}^2 \hat{D}\hat{E}-\hat{D}\hat{C}\hat{E}\hat{C}+\hat{C}\hat{D}\hat{E}\hat{C} \]

Thus, \([\hat{A},\hat{B}]=\hat{C}\hat{D}\hat{C}\hat{E}-\hat{C}^2 \hat{D}\hat{E}-\hat{D}\hat{C}\hat{E}\hat{C}+\hat{C}\hat{D}\hat{E}\hat{C} \).

b. \(\dfrac{d}{dz}\) and \(z \)

Assume that we operate \([\hat{A},\hat{B}]\) on a random function f(z):

\[[\hat{A},\hat{B}]f(z)=\dfrac{d}{dz}\left[zf(z)\right]-z\dfrac{d f}{dz}=\left[f(z)+z\dfrac{df}{dz}\right]-z\dfrac{df}{dz} = f(z)\]

Thus, \([\hat{A},\hat{B}]=1\).

c. \(\dfrac{d^2}{dz^2}\) and \( z \)

\[[\hat{A},\hat{B}]f(z)=\dfrac{d^2}{dz^2}\left[zf(z)\right]-z\dfrac{d^2f}{dz^2}=\dfrac{d}{dz}\left[f(z)+z\dfrac{df}{dz}\right]-z\dfrac{d^2f}{dz^2}\]

\[=\dfrac{df}{dz}+\dfrac{df}{dz}+z\dfrac{d^2f}{dz^2}-z\dfrac{d^2f}{dz^2}=2\dfrac{df}{dz}=2\dfrac{d}{dz}f(z)\]

Thus, \([\hat{A},\hat{B}]=2\dfrac{d}{dz}\).

d. \(\dfrac{d^2}{dz^2}\) and \( z^2 \)

\[[\hat{A},\hat{B}]f(z)=\dfrac{d^2}{dz^2}\left[z^2 f(z)\right]-z^2\dfrac{d^2f}{dz^2}=\dfrac{d}{dz}\left[2zf(z)+z^2\dfrac{df}{dz}\right]-z^2\dfrac{d^2f}{dz^2}\]

\[=2f(z)+2z\dfrac{df}{dz}+2z\dfrac{df}{dz}+z^2\dfrac{d^2f}{dz^2}-z^2\dfrac{d^2f}{dz^2}=2f(z)+4z\dfrac{df}{dz}=(2+4z\dfrac{d}{dz})f(z)\]

Thus, \([\hat{A},\hat{B}]=2+4z\dfrac{d}{dz}\).

e. \( \dfrac{d^2}{dy^2}\) and \(y \)

\[[\hat{A},\hat{B}]f(y)=\dfrac{d^2}{dy^2}\left[yf(y)\right]-y\dfrac{d^2f}{dy^2}=\dfrac{d}{dy}\left[f(y)+y\dfrac{df}{dy}\right]-y\dfrac{d^2f}{dy^2}\]

\[=\dfrac{df}{dy}+\dfrac{df}{dy}+y\dfrac{d^2f}{dy^2}-y\dfrac{d^2f}{dy^2}=2\dfrac{df}{dy}=2\dfrac{d}{dy}f(y)\]

Thus, \([\hat{A},\hat{B}]=2\dfrac{d}{dy}\).

f. \(\dfrac{d}{dz}-z\) and \(\dfrac{d}{dz}+z \)

\(\hat{A}=\dfrac{d}{dz}-z\), \(\hat{B}=\dfrac{d}{dz}+z\)

\[ [\hat{A},\hat{B}] f(z) =\hat{A}\hat{B}f(z)-\hat{B}\hat{A}f(z) = (\dfrac{d}{dz}-z)(\dfrac{d}{dz}+z)f(z) -(\dfrac{d}{dz}+z)(\dfrac{d}{dz}-z)f(z)\]

\[=(\dfrac{d}{dz}-z)\left[\dfrac{df}{dz}+zf(z)\right]-(\dfrac{d}{dz}+z)\left[\dfrac{df}{dz}-zf(z)\right]=\dfrac{d^2f}{dz^2}+\dfrac{d}{dz}[z(f(z)]-z\dfrac{df}{dz}-z^2f(z)-\left[\dfrac{d^2f}{dz^2}-\dfrac{d}{dz}(zf(z))+z\dfrac{df}{dz}-z^2f(z)\right]\]

\[=\dfrac{d^2f}{dz^2}+f(z)+z\dfrac{df}{dz}-z\dfrac{df}{dz}-z^2f(z)-\dfrac{d^2f}{dz^2}+f(z)+z\dfrac{df}{dz}-z\dfrac{df}{dz}+z^2f(z)=2f(z) \]

Thus, \( [\hat{A},\hat{B}]=2\).

g. \(\dfrac{d}{dz}\) and \(\displaystyle \int_{0}^{z} dz \)

\(\hat{A}=\dfrac{d}{dz}\), \(\hat{B}=\int_{0}^{z}dz\)

For \(\hat{B}\),

\(\hat{B}f(z)=\int_{0}^{z}f(z)dz\).

So,

\[[\hat{A},\hat{B}]f(z)=\dfrac{d}{dz}\int_{0}^{z}f(z)dz-\int_{0}^{z}\dfrac{df(z)}{dz}dz=f(z)-\left[f(z)-f(0)\right]=f(0)\]

h. \(\dfrac{1}{2}\) and \(\dfrac{d}{dy} \)

\[[\hat{A},\hat{B}]f(y)=0.5\dfrac{d}{dy}f(y)-\dfrac{d}{dy}\left[0.5f(y)\right]=0.5\dfrac{df}{dy}-0.5\dfrac{df}{dy}=0\]

So \[[\hat{A},\hat{B}]=0\]

(This means \(\hat{A}\) and \(\hat{B}\) commute.)

i. \( x^2 - \dfrac{d^2}{dx^2} \) and \( x - \dfrac{d}{dx} \)

\(\hat{A}=x^2-\dfrac{d^2}{dx^2}\), \(\hat{B}=x-\dfrac{d}{dx}\)

\[ [\hat{A},\hat{B}] f(x) =\hat{A}\hat{B}f(x)-\hat{B}\hat{A}f(x) = (x^2-\dfrac{d^2}{dx^2})(x-\dfrac{d}{dx})f(x) -(x-\dfrac{d}{dx})(x^2-\dfrac{d^2}{dx^2})f(x)\]

\[=(x^2-\dfrac{d^2}{dx^2})(xf(x)-\dfrac{df}{dx})-(x-\dfrac{d}{dx})(x^2f(x)-\dfrac{d^2f}{dx^2})=x^3f(x)-x^2\dfrac{df}{dx}-\dfrac{d}{dx}\left[(f(x)-x\dfrac{df}{dx}\right]+\dfrac{d^3f}{dx^3}-x^3f(x)+x\dfrac{d^2f}{dx^2}+2xf(x)-\dfrac{d^3f}{dx^3}\]

\[=-x^2\dfrac{df}{dx}+2x\dfrac{d^2f}{dx^2}+2xf(x)=(-x^2+2x\dfrac{d^2}{dx^2}+2x))f(x) \]

Thus, \( [\hat{A},\hat{B}]=-x^2+2x\dfrac{d^2}{dx^2}+2x\).

j. \( \hat{p}_z = -i \hbar \dfrac{\partial}{\partial z} \) and \( \hat{L}_z = -i \hbar \left( x \dfrac{\partial}{\partial y} - y \dfrac{\partial}{\partial x} \right) \)

\(\hat{A}=\hat{p}_z = -i \hbar \dfrac{\partial}{\partial z} , \hat{B}=\hat{L}_z = -i \hbar \left( x \dfrac{\partial}{\partial y} - y \dfrac{\partial}{\partial x} \right)\)

\[ [\hat{A},\hat{B}] f(x,y,z) =\hat{A}\hat{B}f(x,y,z)-\hat{B}\hat{A}f(x,y,z) = \left[-i \hbar \dfrac{\partial}{\partial z}\right]\left[-i \hbar \left( x \dfrac{\partial}{\partial y} - y \dfrac{\partial}{\partial x} \right)\right] f(x,y,z) - \left[-i \hbar \left( x \dfrac{\partial}{\partial y} - y \dfrac{\partial}{\partial x} \right)\right] \left[-i \hbar \dfrac{\partial}{\partial z}\right] f(x,y,z)\]

\[ = \hbar^2\dfrac{\partial}{\partial z}\left(x\dfrac{\partial f}{\partial y}-y\dfrac{\partial f}{\partial x}\right) - \hbar^2\left(x\dfrac{\partial}{\partial y}-y\dfrac{\partial }{\partial x}\right)\dfrac{\partial f}{\partial z}=\hbar^2(0-0)-\hbar^2(0-0)=0\]

Thus, \( [\hat{A},\hat{B}] = 0\). In other words, these operators commute.

Q8

For the following molecules identify the number of

• degrees of freedom,
• translational degrees of freedom
• rotational degrees of freedom
• vibrational degrees of freedom

1. \(Ne\)
2. \(C_{60}\)
3. \(N_2\)
4. HCN
5. \(CO_2\)
6. \(UF_6\)

Solution 8:

degrees of freedom = translational degrees of freedom + rotational degrees of freedom + vibrational degrees of freedom

The total number of degrees of freedom is equal to 3n, where n is the number of particles in a body. The number of translational degrees of freedom is equal to 3. The number of rotational degrees of freedom is equal to 3 for nonlinear objects and 2 for linear objects. The number of vibrational degrees of freedom is equal to 3n-6 (which is 3n-3-3) for nonlinear objects and 3n-5 (which is 3n-3-2) for linear objects.

Molecule	# of degrees of freedom (df)	# of translational df	# of rotational df	# of vibrational df
\(Ne\)	3x1=3	3	0	0
\(C_{60}\)	3x60=180	3	3	180-3-3=174
\(N_2\)	3x2=6	3	2	6-3-2=1
\(HCN\)	3x3=9	3	2	9-3-2=4
\(CO_2\)	3x3=9	3	2	9-3-2=4
\(UF_6\)	3x7=21	3	3	21-3-3=15

Q9

The wavefunctions for the quantum mechanical harmonic oscillator \(| \psi_v \rangle\) in atomic units with \(\alpha = 1 \) are expressed as

\[ | \psi_v \rangle = N_v H_v e^{-(x-x_o)^2/2} \]

with

• \(x_o\) is the equilibrium position of the oscillator
• \(N_v\) is a normalization factor for a specific \(v\) value
• \(H_v\) is the Hermite polynomial for a specific \(v\) value (see Table M1)

What is the wavefunction (with determined normalization factor) for the harmonic oscillator in the \(v=0\) state?

Solution 9:

To write out the full wave function we need to find H₀ and N₀, the table of H values can be found in the lecture notes with H₀ equals one. To calculate N₀ we have to normalize \(| \psi_0 \rangle\) .

\[ \int_{-\infty}^{\infty} \psi_0^*(x) \psi_0(x)\ dx = 1 \tag{1}\]

\[ N_0^2 \int_{-\infty}^{\infty} e^{-(x-x_0)^2}dx = 1 \tag{2}\]

We use the substitution y = x-x₀

\[ N_0^2 \int_{-\infty}^{\infty} e^{-(y)^2}dy = 1 \tag{3}\]

\[N_0^2\pi^{1/2} = 1 \tag{4}\]

\[N_0 = \pi^{-1/4} \tag{5}\]

\[ | \psi_0 \rangle = \pi^{-1/4} e^{-(x-x_0)^2/2} \tag{6}\]

Q10

Calculate the expectation value of \( x \) of the quantum harmonic oscillator \(x\) from equilibrium when the oscillator is in the \(v=0\) and \(v=1\) quantum states.

Solution 10:

For the \(v=0\) quantum state the wavefunction and mean displacement are:

\[ | \psi_0 \rangle = \pi^{-1/4} e^{-(x-x_o)^2/2} \tag{7}\]

\[<\hat{x}>_0 = (\frac{1}{\pi})^\frac{1}{2}\int_{-\infty}^{\infty} (x-x_o)e^{-(x-x_o)^2}dx = 0\tag{8}\]

Substitue \(y=x-x_o\),

\[<\hat{x}>_0 = (\frac{1}{\pi})^\frac{1}{2}\int_{-\infty}^{\infty} ye^{-(y)^2}dy = 0\tag{8}\]

This integral is equal to zero because we are integrating an odd function over symmetric limits (\(y\) is an odd function while \(e^{y^2}\) is an even function and an even function times an odd function is odd).

For the \(v=1\) quantum the wavefunction and mean displacement are:

\[ | \psi_1 \rangle = (\frac{4}{\pi})^\frac{1}{4} 2xe^{-(x)^2/2} \tag{9}\]

\[<\hat{x}>_1 = 4*(\frac{4}{\pi})^\frac{1}{2}\int_{-\infty}^{\infty} x^3e^{-(x)^2}dx = 0\tag{10}\]

Again the integral is zero because we are integrating an odd function over symmetric limits.

As they are both zero there is no difference between the mean displacements because both are symmetric around zero.

Q11

Calculate the expectation value of \(x^2 \) (i.e., \(\langle x^2 \rangle\)) of the quantum harmonic oscillator \(x\) from equilibrium when the oscillator is in the \(v=0\) and in the \(v=1\) quantum states.

Solution 11:

Using the same \(| \psi_0 \rangle\) and \(| \psi_1 \rangle\) from the previous problem the mean displacements squared are:

\[<\hat{x}^2>_1 = 4*(\frac{4}{\pi})^\frac{1}{2}\int_{-\infty}^{\infty} x^4e^{-(x)^2}dx = 4*(\frac{4}{\pi})^\frac{1}{2} \times \frac{3\pi^\frac{1}{2}}{4} =6\tag{11}\]

\[<\hat{x}^2>_0 = (\frac{1}{\pi})^\frac{1}{2}\int_{-\infty}^{\infty} x^2e^{-(x)^2}dx = (\frac{1}{\pi})^\frac{1}{2} \times \frac{\pi^\frac{1}{2}}{2} = \frac{1}{2}\tag{12}\]

The difference in the mean displacement squared is due to the probability density of \(| \psi_1 \rangle\) being wider than the probability density of \(| \psi_0 \rangle\) as can be seen on the graphs in the lecture notes.

Q12

Use the answers from Q10 and Q11 to determine the uncertainty of position of a particle following the harmonic oscillator with \(v=0\)?

Solution 12:

\[\Delta x_0 = (<x^2> - <x>^2)^{1/2}\]

\[\Delta x_0 = {1/2}^{1/2}\]

Q13

A particle with an effective mass of \(1 \times 10^{-28} \;kg\) oscillates in a well according to the quantum harmonic oscillator, the energy levels are separated by \(2.5 \times 10^{-24}\; J\). What is the force constant for the oscillator? What is the zero point energy of this oscillator?

Solution 13:

\[\Delta E = 2.5 \times 10^{-24}\; J\]

\[\Delta E = \hbar\omega\]

\[\omega=\dfrac{\Delta E}{\hbar}\]

\[\omega = (K/m)^{1/2}\]

\[K = m\omega^2=m\left(\dfrac{\Delta E}{\hbar}\right)^2\]

\[K = 5.62 \times 10^{-8}\; N/M\]

The zero point energy, or the lowest possible energy for the harmonic oscillator is:

\[E = 1/2\hbar\omega\]

\[E = 1/2\Delta E\]

\[E = 1.25 \times 10^{-24}\; J\]