Homework 8A
- Page ID
- 143083
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Q1
A basis function is an element of a particular basis for a function space. Every continuous function in the function space can be represented as a linear combination of basis functions, just as every vector in a vector space can be represented as a linear combination of basis vectors.
- List three basis that can be used to expand a general 1-D function (Hint: consider Taylor, Fourier and Laplace expansions).
- Write the mathematical expansion formula for each of the three expansions above
- What is the definition of a complete basis?
- Are the three basis systems identified above complete basis for describing 1-D functions?
Q2
The wavefunction can be expanded into the complete set of basis of eigenstates of the Hamiltonian:
\[| \Psi \rangle =\sum_i c_i | \phi_i \rangle \]
What is the general expression of the off diagonal (\(i \neq j\)) and diagonal (\(i = j\)) matrix elements for the Hamiltonian in the basis set of its eigenstates?
\[H_{ij} = \langle \phi_i | \hat{H} | \phi_j \rangle \]
(Hint: Apply the Hamiltonian \(\hat{H}\) on this arbitrary wavefuction \(| \Psi \rangle\) and its bra version \(\langle \Psi | \)).
Q3
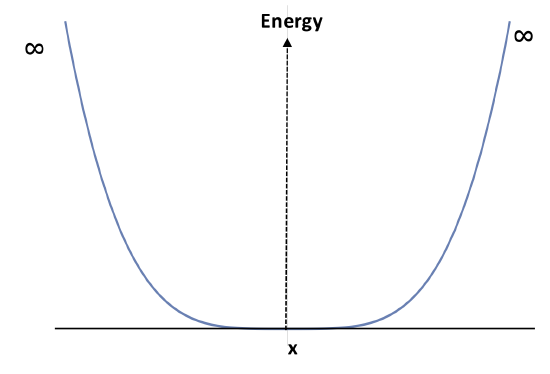
a. Estimate the ground state energy and wavefunction for a particle in a box using the variational method with the following trial wavefunction, where N is the normalization constant and \(\beta\) is a variational parameter that should be minimized.
\[ | \psi \rangle = N \exp(-\beta x^2)\]
b. Is this a good trial wavefunction for this approximation (justify your answer)?
c. Why is this not a good wavefunction?
d. Can you solve this problem both analytically and numerically? Pay careful attention to limits of integration.
Q4
Using the variational method approximation, find the ground state energy of a particle in a box using this trial function:
\[ \psi = N \cos \left(\frac{\pi x}{L}\right) \]
Compare this to the true ground state energy for a particle in a box.
Q5
Given the following potential energy for a molecular vibration:
\[ V(x) = \frac{1}{2} kx^2 + c_1 x^3 + c_2 x^ 4 + c_3x^5 \]
Use first order perturbation theory to calculate the first three energy levels of an oscillating molecule with this potential. \( \alpha =m \omega / \hbar \) :
\[ \psi_0 (x) = \left( \frac{\alpha}{\pi} \right)^{1/4} \exp \left(-\frac{\alpha x^2}{2}\right) \]
\[ \psi_1 (x) = \left(\frac{4\alpha^3}{\pi} \right)^{1/4} x \exp \left(-\frac{\alpha x^2}{2}\right) \]
\[ \psi_2 (x) = \left(\frac{\alpha}{4\pi} \right)^{1/4} (2\alpha x^2 - 1) \exp \left(-\frac{\alpha x^2}{2}\right) \]
Given these results, what can you say about the perturbation for a harmonic oscillator?
Q6
Consider a particle in the following 1D box. The potential in this box has the form:
For a PIB:
\[ E^0 = \frac{n^2 h^2}{8mL^2} \]
\[ \psi^0 = \left( \frac{2}{L} \right)^{1/2} \sin \left( \frac{n\pi x}{L} \right) \]
- Calculate the first order perturbation given this potential.
- Feel free to calculate the first order wavefunction. (Optional)
Q7
Now assume the parabolic potential well for the particle in a box above becomes broader as shown:
We can use a quartic function function to represent this potential as shown below. Using the first order perturbation theory for particle in a box, calculate the ground-state energy:
\[ V(x)=c x^4 \quad 0<x< b \]
- How large of an effect on the energy is the perturbation of a curved wall?
- Feel free to calculate the first order wavefunction. (Optional)
Q8
An electron moving in a conjugated \(\pi\) framework of a molecule (such as an alkene like polyacetylene) can be approximated as an electron in a box of length \(L\). If an externally applied electric field of strength \(\epsilon\)
\[\overrightarrow{F}= e\epsilon\]
that is oriented along the \(x\) axis (the length of the box), it interacts with the negatively charged electron via the following perturbation to the potential energy
\[V= e\epsilon\left( x-\frac{L}{2} \right)\]
where \(x\) is the position of the electron in the box, \(\epsilon\) is the field strength, and \(e\) is the electron charge. Calculate the first order perturbation to the energy of the ground-state wavefunction.
Q9
A NMR (nuclear magnetic resonance) experiment on a compound with two proton (e.g., two protons in H2) can be illustrated using a secular determinant. For two equivalent spin 1/2 particles (e.g., protons), the simple product functions are:
\[ \psi_1 = \alpha(1) \alpha(2) \]
\[ \psi_2 = \alpha(1) \beta(2) \]
\[ \psi_3 = \beta(1) \alpha(2) \]
\[ \psi_4 = \beta(1) \beta(2) \]
In operator form, the magnetic Hamiltonian for this system is:
\[ \hat{H} = -\left[\sum_{i} \omega_i \hat{I}_{zi} + \sum \sum_{i<j} J_{ij}\left[\hat{I}_{zi}\hat{I}_{zj} + \frac{1}{2}\left(\hat{I}_i^+\hat{I}_j^- +\hat{I}_i^-\hat{I}_j^-\right)\right]\right] \]
Working out the matrix elements determines the following eigenvalues:
\[ \begin{align} H_{11} &= \langle \psi_1 | \hat{H} | \psi_1 \rangle \\[5pt] &= -\left(\frac{1}{2}\omega_1 + \frac{1}{2}\omega_2 + \frac{1}{4}J_{12} \right) \\[5pt] H_{12} &= \langle \psi_1 | \hat{H} | \psi_2 \rangle = 0 \\[5pt] H_{13} &= \langle \psi_1 | \hat{H} | \psi_3 \rangle = 0 \\[5pt] H_{14} &= \langle \psi_1 | \hat{H} | \psi_4 \rangle = 0 \\[5pt] H_{22} &= \langle \psi_2 | \hat{H} | \psi_2 \rangle \\[5pt] &= -\left(\frac{1}{2}\omega_1 - \frac{1}{2}\omega_2 - \frac{1}{4}J_{12} \right) \\[5pt] H_{23} &= \langle \psi_2 | \hat{H} | \psi_3 \rangle = -\frac{1}{2}J_{12} \\[5pt] H_{24} &= \langle \psi_2 | \hat{H} | \psi_4 \rangle = 0 \\[5pt] H_{33} &= \langle \psi_3 | \hat{H} | \psi_3 \rangle \\[5pt] &= -\left(-\frac{1}{2}\omega_1 + \frac{1}{2}\omega_2 - \frac{1}{4}J_{12} \right) \\[5pt] H_{34} &= \langle \psi_3 | \hat{H} | \psi_4 \rangle = 0 \\[5pt] H_{44} &= \langle \psi_4 | \hat{H} | \psi_4 \rangle \\[5pt] &= -\left(-\frac{1}{2}\omega_1 - \frac{1}{2}\omega_2 + \frac{1}{4}J_{12} \right) \end{align}\]
where \(\omega_1\), \(\omega_2\) and \(J_{12}\) are constants.
- Write out the resulting secular determinant.
- Assume the nuclei are equivalent. What are the roots / energies calculated from solving the secular determinant? (Hint: This problem is wordy but easier than it looks.)
Q10
Normalize this two-electron wavefunction
\[ |\Psi(1,2) \rangle = \begin{vmatrix}\alpha (1) & \alpha (2) \\\ \beta(1) & \beta (2) \end{vmatrix}\]