Homework 4
- Page ID
- 143067
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Template:HideTOC Template:HideTOCQ1
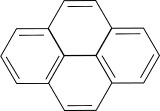
Electrons are delocalized in the pi-orbitals of Polycyclic aromatic hydrocarbons. This becomes a particle in the box problem. Since the molecule is confined within a plane, a two-dimensional particle in a box model is a good approximation of a delocalized electron. Assume the boundary of the box is one C-H bond length beyond the carbon rings to contain the hydrogen atoms in the box. Hint: Use trigonometry for the dimensions.
Calculate the first three electronic transitions for Benzo[def]phenanthrene (bond length 1.42 Angstroms).
Q2
Given a quantum wire made from Silicon Telluride (Si2Te3) with a 1D width of 7.5 nm,
a. What is the energy required (in electron volts) to make a transition from the state n=1 to n=2?
b. The measured value for this transition is about 1.9 eV (652.5nm). What would the mass of the electron be if this were the energy measured?
Q3
Given a quantum wire made from Silicon Telluride (Si2Te3) with a 1D width of 75 nm,
a. What is the energy required (in electron volts) to make a transition from the state n=1 to n=2?
b. Comment on how the energy has changed as the size of the box for silicon telluride has changed.
Q4
Find the normalization constant \(B\) in the following wavefunctions:
- \[ \psi(x) = Be^{ikx}\]
- \[ \psi(x) = Be^{-ikx}e^{-2x^2/2a^2}\]
Q5
Show that the eigenstates to a particle in a 1D box with infinite potential satisfy the orthogonormality relationship:
\[ \int_{-\infty}^{\infty} \psi_n^*(x) \psi_m(x)\; dx = 1 \; \text{if } m=n\]
and
\[ \int_{-\infty}^{\infty} \psi_n^*(x) \psi_m(x)\; dx = 0 \; \text{if } m \neq n\]
Q6
Evaluate the following commutators \( [\hat{A}, \hat{B}] \) for the following pair of operators:
- \(\dfrac{d}{dx}\) and \(x \)
- \(\dfrac{d}{dx}\) and \(y \)
- \(\dfrac{d^2}{dx^2}\) and \( x \)
- \(\dfrac{d^2}{dx^2}\) and \( x^2 \)
- \(\dfrac{d}{dx}\) and \(\displaystyle \int_{0}^{x} dx \)
- \(\dfrac{1}{2}\) and \(\dfrac{d}{dz} \)
- \( \hat{p}_z = -i \hbar \dfrac{\partial}{\partial z} \) and \( \hat{L}_z = -i \hbar \left( x \dfrac{\partial}{\partial y} - y \dfrac{\partial}{\partial x} \right) \)
Q7
For the following molecules identify the number of
- degrees of freedom,
- translational degrees of freedom
- rotational degrees of freedom
- vibrational degrees of freedom
- \( Kr \)
- HF
- \(C_{60}\)
- \(H_2\)
- \(SF_6\)
- \(UO_2\)
Q8
The wavefunctions for the quantum mechanical harmonic oscillator \(| \psi_v \rangle\) in atomic units with \(\alpha = 1 \) are expressed as
\[ | \psi_v \rangle = N_v H_v e^{-(x-x_o)^2/2} \]
with
- \(x_o\) is the equilibrium position of the oscillator
- \(N_v\) is a normalization factor for a specific \(v\) value
- \(H_v\) is the Hermite polynomial for a specific \(v\) value (see Table M1)
What is the wavefunction (with determined normalization factor) for the harmonic oscillator in the \(v=0\) state?
Q9
Calculate the expectation value of \( x \) of the quantum harmonic oscillator \(x\) from equilibrium when the oscillator is in the \(v=0\) and \(v=1\) quantum states.
Q10
Calculate the expectation value of \(x^2 \) (i.e., \(\langle x^2 \rangle\)) of the quantum harmonic oscillator \(x\) from equilibrium when the oscillator is in the \(v=0\) and in the \(v=1\) quantum states.
Q111
Use the answers from Q8 and Q9 to determined the uncertainty of position of a particle following the harmonic oscillator with \(v=0\)?