4: Complex Ion Structure and Geometry (Worksheet)
- Page ID
- 81472
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\(\newcommand{\ket}[1]{\left| #1 \right>} \)
\( \newcommand{\bra}[1]{\left< #1 \right|} \)
\( \newcommand{\braket}[2]{\left< #1 \vphantom{#2} \right| \left. #2 \vphantom{#1} \right>} \)
\( \newcommand{\qmvec}[1]{\mathbf{\vec{#1}}} \)
\( \newcommand{\op}[1]{\hat{\mathbf{#1}}}\)
\( \newcommand{\expect}[1]{\langle #1 \rangle}\)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.
Introduction to Isomerization
As you have seen in the chemistry of carbon‐containing compounds, often there are several isomers possible for the same compound formula. Even when atoms are connected in the same order it is possible that we have not uniquely described the structure of the molecule. Isomers have unique properties:
- are two or more molecules or ions that contain the same number and kinds of atoms (identical molecular formulas), but the atoms are arranged differently (i.e., the structures are non-superimposable)
- have different physical and/or chemical properties,
- do not exist for all coordination compounds, and
- are generally categorized as either structural isomers or stereoisomers.
Structural isomers: isomers that have the same molecular formula, but one or more bonds is/are different (i.e., the connectivity between atoms is different). There are two types of structural isomers: ionization, coordination and linkage isomers.
Stereoisomers: contain the same number and kinds of atoms, and the same number and kinds of bonds (i.e., the connectivity between atoms is the same), but the atoms are arranged differently in space. There are two types of stereoisomers: geometric isomers, and optical isomers.
Structural Isomers: Ionization Isomers
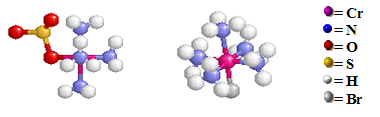
The sulfate group inside the coordination sphere on the left structure is bonded to the Cr atom by an O atom. The bromide counter ion needed to maintain charge neutrality for the compound with the complex ion [Cr(NH3)5(OSO3)]+ is not shown in the above structure. For the right structure, the bromine ion is bonded to the Cr atom at the bottom of the octahedral structure and has inside the coordination sphere displacing the sulfato group. The resulting sulfate counter ion is not shown in the either structures.
Structural Isomers: Coordination Isomers
Coordination isomers are two or more coordination compounds in which the composition within the coordination sphere (i.e., the metal atom plus the ligands that are bonded to it) is different (i.e., the connectivity between atoms is different). Not all coordination compounds have coordination isomers. Coordination sphere isomers have different physical and chemical properties.

For example, the cis-[Pt(NH3)2Cl4][Pt(NH3)4] coompound on the left has the ammine groups are bonded to the Pt ion by N atoms inside both coordination spheres (Note that only the cationic coordination sphere contains chloro group ligands) and the cis-[Pt(NH3)4Cl2] cis- [Pt(NH3)2Cl2] compound on the right has two chloro ligands originally bonded to the Pt atom within the cationic coordination sphere have exchanged with two of the ammine groups in the anionic coordination sphere
Structural Isomers: Linkage Isomers
Linkage isomers are coordination compounds in which the donor atom of at least one of monodentate ligands capable of bonding through two or more donor atoms is different. These ligands are referred to as ambidentate ligands. Some of these type ligands are listed below. The standard form of the name is assigned to the linkage involving the less electronegative donor atom of the ligand. The variant form of the name is assigned to the linkage involving the more electronegative atom of the ligand. Linkage isomers have different physical and chemical properties.
| ligand | Lewis Structure | name | donor atom |
|---|---|---|---|
| CN- | 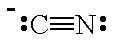 |
cyano | C |
| isocyano | N | ||
| SCN- | 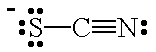 |
thiocyanato | S |
| isothiocyanato | N | ||
| NO2- | 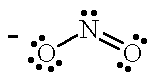 |
nitro | N |
| nitrito | O |
For the tetraamminechloronitrocobalt (II) ion (left), the less electronegative nitrogen of the nitrous oxide ligand is bonded to the Co atom. The nitrous oxide ligand is written as "NO2" in the molecular formula with the N atom nearest to the Co symbol to indicate that the N is the donor atom and the name nitro is used when naming the coordination complex. For [Co(NH3)4Cl(ONO)]+, when the more electronegative O atom of the ambidentate nitrous oxide ligand is bonded to the Co atom the name is changed to nitrito. The nitrous oxide ligand is written as "ONO" in the molecular formula with the O atom nearest to the Co symbol to indicate that the O atom is the donor atom.

Stereoisomers: Geometric Isomers
Geometric isomers are two or more coordination compounds which contain the same molecular formula, and bonds, but have different spatial ordering of the atoms. The square planar molecule, Pt(NH3)2Cl2, the two ammonia ligands (or the two chloride ligands) can be adjacent to one another or opposite one another. To change between the two isomers bonds must be broken and new bonds formed.
For example, these two square planar structures contain the same molecular structure and bonds but are non-superimposable. The isomer in which like ligands are adjacent to one another is called the cis isomer. The isomer in which like ligands are opposite one another is called the trans isomer.
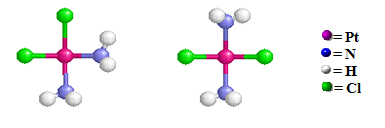
The two ammine ligands on the left left structure are adjacent to one another and the two chloro ligands are adjacent to one another. This compound is used medicinally to treat certain types of cancer. (tradename: "cisplatin"). The two ammine ligands on the right strucure are opposite one another and the two chloro ligands are opposite one another. The like ligands are on opposite sides of the central metal ion. This compound does not exhibit any anti-tumor activity
Octahedral complexes can exhibit another type of geometric isomerism called mer-fac isomerism.
- mer isomerism involves all three similar ligand lying in the same plane, or meridinal like a globe.
- fac facial involves a grouping of three similar ligands that are arranged on a triangular face of the octrahedron
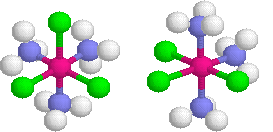
Stereoisomers: Optical Isomers
Optical isomers are two compounds which contain the same number and kinds of atoms, and bonds (i.e., the connectivity between atoms is the same), and different spatial arrangements of the atoms, with non-superimposable mirror images. Each non-superimposable mirror image structure is called an enantiomer. Molecules or ions that exist as optical isomers are called chiral. Separate equimolar solutions of the two isomers rotate plane polarized light by equal angles but in opposite directions. The phenomenon of rotation of polarized light is called optical activity.
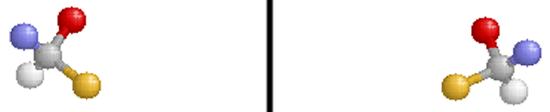
Note that the molecule on the right is the reflection of the molecule on the left (through the mirror plane indicated by the black vertical line). These two structures are non-superimposable and are, therefore, different compounds.
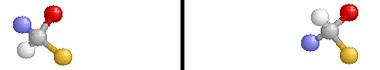
Pure samples of enantiomers have identical physical properties (e.g., boiling point, density, freezing point). Chiral molecules and ions have different chemical properties only when they are in chiral environments. Optical isomers get their name because the plane of plane-polarized light that is passed through a sample of a pure enantiomer is rotated. The plane is rotated in the opposite direction but with the same magnitude when plane-polarized light is passed through a pure sample containing the other enantiomer of a pair.
Q4.1
Draw the structure for each of the following complex compounds or ions.
- trans-dichlorobis(ethylenediamine)cobalt (III) chlorate
- [Co (NH3)6] Cl3
- cis-diammine-trans-dibromo-cis-dichloroplatinum (VI) bromate
- tetraaquacadmium (II) nitrate
- mer-[Fe (NC)3(ONO)3]-4
- sodium tetraisocyanocuprate (I)
- Ag4fac-[Fe (NC)3(ONO)3]
- Both optical isomers for cis-aqua-cis-carbonyl-cis-cyanonickel (II)
Q4.2
For each of these compounds indicate if it may be chiral or not (hint: this may depend on the specific isomer considered)?
- \(\ce{Co(NH3)3(CN)3}\)
- \(\ce{[Cr(NH3)2(OH2)2(CN)2]^{2+}}\)
- \(\ce{cis-Pd(NH3)2(Cl)2}\)
- \(\ce{trans-[Fe(en)2(Cl)2]^{+}}\)
- \(\ce{cis-[Mn(en)2(Cl)2]}\)
Q4.3
What is the total number of stereoisomers possible for the \(\ce{[Co(NH3)2(Br)2(en)]^{+}}\) complex ion?
- 3
- 4
- 5
- 6
- 7
Q4.4
For each of the following complexes, draw all geometric isomers and label. Indicate which exist as a pair of enantiomers.
- \(\ce{[Cr(H_2O)_3(OH)_2Cl]}\)
- \(\ce{[M(NH_3)_2Cl_2F_2] }\)
- \(\ce{[Ni(en)(ox)(H_2O)(NH_3)]}\)


