15.3: Relationships Involving Equilibrium Constants
- Page ID
- 42210
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To know the relationship between the equilibrium constant and the rate constants for the forward and reverse reactions.
- To understand how different phases affect equilibria.
Relating Stoichiometry and Equilibrium Constants
It is important to remember that an equilibrium constant is always tied to a specific chemical equation, and if we write the equation in reverse or multiply its coefficients by a common factor, the value of \(K\) will change. Fortunately, the rules are very simple:
- Writing the equation in reverse will invert the equilibrium expression and
- Multiplying the coefficients by a common factor will raise K to the corresponding power.
Here are some of the possibilities for the reaction involving the equilibrium between gaseous water and its elements:
| \(2 H_2 + O_2\rightleftharpoons 2 H_2O\) | \(10 H_2 + 5 O_2 \rightleftharpoons 10 H_2O\) | \(H_2 + ½ O_2 \rightleftharpoons H_2O\) | \(H_2O \rightleftharpoons H_2 + ½ O_2\) |
|
\(K_p = \dfrac{P_{H_2O}^2}{P_{H_2}^2P_{O_2}}\) |
\(K_p = \dfrac{P_{H_2O}^{10}}{P_{H_2}^{10}P_{O_2}^5}\) \(= \left(\dfrac{P_{H_2O}^2}{P_{H_2}^2P_{O_2}}\right)^{5}\) |
\(K_p = \dfrac{P_{H_2O}}{P_{H_2}P_{O_2}^{1/2}}\) \(= \left(\dfrac{P_{H_2O}^2}{P_{H_2}^2P_{O_2}}\right)^{1/2}\) |
\(K_p = \dfrac{P_{H_2}P_{O_2}^{1/2}}{P_{H_2O}}\) \(= \left(\dfrac{P_{H_2O}^2}{P_{H_2}^2P_{O_2}}\right)^{-1/2}\) |
Many chemical changes can be regarded as the sum or difference of two or more other reactions. If we know the equilibrium constants of the individual processes, we can easily calculate that for the overall reaction according to the following rule:
The equilibrium constant for the sum of two or more reactions is the product of the equilibrium constants for each of the steps.
Calculate the value of \(K\) for the reaction
\[CaCO_{3(s)} + H^+_{(aq)} \rightarrow Ca^{2+}_{(aq)} + HCO^–_{3(aq)}\]
given the following equilibrium constants:
|
\(CaCO_{3(s)} \rightleftharpoons Ca^{2+}_{(aq)} + CO^{2–}_{3(aq)}\) |
\(K_1 = 10^{–6.3}\) |
|
\(HCO^–_{3(aq)} \rightleftharpoons H^+_{(aq)} + CO^{2–}_{3(aq)}\) |
\(K_2 = 10^{–10.3}\) |
Solution
The net reaction is the sum of reaction 1 and the reverse of reaction 2:
|
\(CaCO_{3(s)} \rightleftharpoons Ca^{2+}_{(aq)} + CO^{2–}_{3(aq)}\) |
\(K_1 = 10^{–6.3}\) |
|
\( H^+_{(aq)} + CO^{2–}_{3(aq)} \rightleftharpoons HCO^–_{3(aq)} \) |
\(K_{–2} = 10^{–(–10.3)}\) |
|
\(CaCO_{3(s)} + H^+_{(aq)} \rightarrow Ca^{2+}_{(aq)} + HCO^–_{3(aq)}\) |
\(K = \dfrac{K_1}{K_2} = 10^{(-6.3+10.3)} =10^{+4.0}\) |
Comment:
This net reaction describes the dissolution of limestone by acid; it is responsible for the eroding effect of acid rain on buildings and statues. This an example of a reaction that has practically no tendency to take place by itself (small K1) being "driven" by a second reaction having a large equilibrium constant (K–2). From the standpoint of the Le Chatelier principle, the first reaction is "pulled to the right" by the removal of carbonate by hydrogen ion. Coupled reactions of this type are widely encountered in all areas of chemistry, and especially in biochemistry, in which a dozen or so reactions may be linked.
The synthesis of HBr from hydrogen and liquid bromine has an equilibrium constant \(K_p = 4.5 \times 10^{15}\) at 25°C. Given that the vapor pressure of liquid bromine is 0.28 atm, find \(K_p\) for the homogeneous gas-phase reaction at the same temperature.
Solution
The net reaction we seek is the sum of the heterogeneous synthesis of HBr and the reverse of the vaporization of liquid bromine:
| \(H_{2(g)} + Br_{2(l)} \rightleftharpoons 2 HBr_{(g)}\) | \(K_p = 4.5\times 10^{15}\) |
| \(Br_{2(g)} \rightleftharpoons Br_{2(l)}\) | \(K_p = (0.28)^{–1}\) |
| \(H_{2(g)} + Br_{2(g)} \rightleftharpoons 2 HBr_{(g)}\) | \(K_p = 1.6 \times 10^{19}\) |
Relationships Involving Equilibrium Constants: https://youtu.be/2vZDpXX1zr0
Equilibria Involving Gases
For reactions that involve species in solution, the concentrations used in equilibrium calculations are usually expressed in moles/liter. For gases, however, the concentrations are usually expressed in terms of partial pressures rather than molarity, where the standard state is 1 atm of pressure. The symbol \(K_p\) is used to denote equilibrium constants calculated from partial pressures. For the general reaction \(aA+bB \rightleftharpoons cC+dD\), in which all the components are gases, the equilibrium constant expression can be written as the ratio of the partial pressures of the products and reactants (each raised to its coefficient in the chemical equation):
\[K_p=\dfrac{(P_C)^c(P_D)^d}{(P_A)^a(P_B)^b} \label{15.3.1}\]
Thus \(K_p\) for the decomposition of \(N_2O_4\) is as follows:
\[K_p=\dfrac{(P_{NO_2})^2}{P_{N_2O_4}} \label{15.3.2}\]
Like K, \(K_p\) is a unitless quantity because the quantity that is actually used to calculate it is an “effective pressure,” the ratio of the measured pressure to a standard state of 1 bar (approximately 1 atm), which produces a unitless quantity.The “effective pressure” is called the fugacity, just as activity is the effective concentration.
Because partial pressures are usually expressed in atmospheres or mmHg, the molar concentration of a gas and its partial pressure do not have the same numerical value. Consequently, the numerical values of \(K\) and \(K_p\) are usually different. They are, however, related by the ideal gas constant (\(R\)) and the absolute temperature (\(T\)):
\[ \color{red} {K_p = K_c(RT)^{Δn} \label{15.3.3}}\]
where \(K\) is the equilibrium constant expressed in units of concentration and \(Δn\) is the difference between the numbers of moles of gaseous products and gaseous reactants (\(n_p − n_r\)). The temperature is expressed as the absolute temperature in Kelvin. According to Equation 15.3.3, \(K_p = K\) only if the moles of gaseous products and gaseous reactants are the same (i.e., \(Δn = 0\)). For the decomposition of \(N_2O_4\), there are 2 mol of gaseous product and 1 mol of gaseous reactant, so \(Δn = 1\). Thus, for this reaction,
\[K_p = K(RT)^1 = K_cRT \label{15.3.4}\]
The equilibrium constant for the reaction of nitrogen and hydrogen to give ammonia is 0.118 at 745 K. The balanced equilibrium equation is as follows:
\[N_{2(g)}+3H_{2(g)} \rightleftharpoons 2NH_{3(g)}\]
What is \(K_p\) for this reaction at the same temperature?
Given: equilibrium equation, equilibrium constant, and temperature
Asked for: \(K_p\)
Strategy:
Use the coefficients in the balanced chemical equation to calculate \(Δn\). Then use Equation 15.3.3 to calculate \(K\) from \(K_p\).
Solution:
This reaction has 2 mol of gaseous product and 4 mol of gaseous reactants, so \(\Delta{n} = (2 − 4) = −2\). We know \(K\), and \(T = 745\; K\). Thus, from Equation 15.2.15, we have the following:
\[K_p=K(RT)^{−2}=\dfrac{K}{(RT)^2}=\dfrac{0.118}{\{ [0.08206(L \cdot atm)/(mol \cdot K)][745\; K]\}^2}=3.16 \times 10^{−5}\]
Because \(K_p\) is a unitless quantity, the answer is \( K_p = 3.16 \times 10^{−5}\).
Calculate \(K_p\) for the reaction
\[2SO_{2(g)}+O_{2(g)} \rightleftharpoons 2SO_{3(g)}\]
at 527°C, if \(K = 7.9 \times 10^4\) at this temperature.
Answer: \(K_p = 1.2 \times 10^3\)
Converting Kc to Kp: https://youtu.be/_2WVnlqXrV4
Combining Equilibrium Constant Expressions
Chemists frequently need to know the equilibrium constant for a reaction that has not been previously studied. In such cases, the desired reaction can often be written as the sum of other reactions for which the equilibrium constants are known. The equilibrium constant for the unknown reaction can then be calculated from the tabulated values for the other reactions.
To illustrate this procedure, let’s consider the reaction of \(N_2\) with \(O_2\) to give \(NO_2\). This reaction is an important source of the \(NO_2\) that gives urban smog its typical brown color. The reaction normally occurs in two distinct steps. In the first reaction (1), \(N_2\) reacts with \(O_2\) at the high temperatures inside an internal combustion engine to give \(NO\). The released \(NO\) then reacts with additional \(O_2\) to give \(NO_2\) (2). The equilibrium constant for each reaction at 100°C is also given.
- \(N_{2(g)}+O_{2(g)} \rightleftharpoons 2NO_{(g)}\;\; K_1=2.0 \times 10^{−25}\)
- \(2NO_{(g)}+O_{2(g)} \rightleftharpoons 2NO_{2(g)}\;\;\;K_2=6.4 \times 10^9\)
Summing reactions (1) and (2) gives the overall reaction of \(N_2\) with \(O_2\):
- \(N_{2(g)}+2O_{2(g)} \rightleftharpoons 2NO_{2(g)} \;\;\;K_3=?\)
The equilibrium constant expressions for the reactions are as follows:
\[K_1=\dfrac{[NO]^2}{[N_2][O_2]}\;\;\; K_2=\dfrac{[NO_2]^2}{[NO]^2[O_2]}\;\;\; K_3=\dfrac{[NO_2]^2}{[N_2][O_2]^2} \label{15.3.5}\]
What is the relationship between \(K_1\), \(K_2\), and \(K_3\), all at 100°C? The expression for \(K_1\) has \([NO]^2\) in the numerator, the expression for \(K_2\) has \([NO]^2\) in the denominator, and \([NO]^2\) does not appear in the expression for \(K_3\). Multiplying \(K_1\) by \(K_2\) and canceling the \([NO]^2\) terms,
\[ K_1K_2=\dfrac{\cancel{[NO]^2}}{[N_2][O_2]} \times \dfrac{[NO_2]^2}{\cancel{[NO]^2}[O_2]}=\dfrac{[NO_2]^2}{[N_2][O_2]^2}=K_3 \label{15.3.6}\]
Thus the product of the equilibrium constant expressions for \(K_1\) and \(K_2\) is the same as the equilibrium constant expression for \(K_3\):
\[K_3 = K_1K_2 = (2.0 \times 10^{−25})(6.4 \times 10^9) = 1.3 \times 10^{−15} \label{15.3.7}\]
The equilibrium constant for a reaction that is the sum of two or more reactions is equal to the product of the equilibrium constants for the individual reactions. In contrast, recall that according to Hess’s Law, \(ΔH\) for the sum of two or more reactions is the sum of the ΔH values for the individual reactions.
To determine \(K\) for a reaction that is the sum of two or more reactions, add the reactions but multiply the equilibrium constants.
The following reactions occur at 1200°C:
- \(CO_{(g)}+3H_{2(g)} \rightleftharpoons CH_{4(g)}+H_2O_{(g)} \;\;\;K_1=9.17 \times 10^{−2}\)
- \(CH_{4(g)}+2H_2S_{(g)} \rightleftharpoons CS_{2(g)}+4H_{2(g})\;\;\; K_2=3.3 \times 10^4\)
Calculate the equilibrium constant for the following reaction at the same temperature.
- \(CO_{(g)}+2H_2S_{(g)} \rightleftharpoons CS_{2(g)}+H_2O_{(g)}+H_{2(g)}\;\;\; K_3=?\)
Given: two balanced equilibrium equations, values of \(K\), and an equilibrium equation for the overall reaction
Asked for: equilibrium constant for the overall reaction
Strategy:
Arrange the equations so that their sum produces the overall equation. If an equation had to be reversed, invert the value of \(K\) for that equation. Calculate \(K\) for the overall equation by multiplying the equilibrium constants for the individual equations.
Solution:
The key to solving this problem is to recognize that reaction 3 is the sum of reactions 1 and 2:
\[CO_{(g)}+ \cancel{3H_{2(g)}} \rightleftharpoons \cancel{CH_{4(g)}} + H_2O_{(g)}\]
\[\cancel{CH_{4(g)}} +2H_2S_{(g)} \rightleftharpoons CS_{2(g)} + \cancel{3H_{2(g)}} + H_{2(g)}\]
\[ CO_{(g)} + 3H_{2(g)} \rightleftharpoons CS_{2(g)}+H_2O_{(g)}+H_{2(g)}\]
The values for \(K_1\) and \(K_2\) are given, so it is straightforward to calculate \(K_3\):
\[K_3 = K_1K_2 = (9.17 \times 10^{−2})(3.3 \times 10^4) = 3.03 \times 10^3\]
In the first of two steps in the industrial synthesis of sulfuric acid, elemental sulfur reacts with oxygen to produce sulfur dioxide. In the second step, sulfur dioxide reacts with additional oxygen to form sulfur trioxide. The reaction for each step is shown, as is the value of the corresponding equilibrium constant at 25°C. Calculate the equilibrium constant for the overall reaction at this same temperature.
- \(\frac{1}{8}S_{8(s)}+O_{2(g)} \rightleftharpoons SO_{2(g)}\;\;\; K_1=4.4 \times 10^{53}\)
- \(SO_{2(g)}+\frac{1}{2}O_{2(g)} \rightleftharpoons SO_{3(g)}\;\;\; K_2=2.6 \times 10^{12}\)
- \(\frac{1}{8}S_{8(s)}+\frac{3}{2}O_{2(g)} \rightleftharpoons SO_{3(g)}\;\;\; K_3=?\)
Answer: \(K_3 = 1.1 \times 10^{66}\)
Heterogeneous Equilibria
When the products and reactants of an equilibrium reaction form a single phase, whether gas or liquid, the system is a homogeneous equilibrium. In such situations, the concentrations of the reactants and products can vary over a wide range. In contrast, a system whose reactants, products, or both are in more than one phase is a heterogeneous equilibrium, such as the reaction of a gas with a solid or liquid.
Because the molar concentrations of pure liquids and solids normally do not vary greatly with temperature, their concentrations are treated as constants, which allows us to simplify equilibrium constant expressions that involve pure solids or liquids.The reference states for pure solids and liquids are those forms stable at 1 bar (approximately 1 atm), which are assigned an activity of 1. (Recall that the density of water, and thus its volume, changes by only a few percentage points between 0°C and 100°C.)
Consider the following reaction, which is used in the final firing of some types of pottery to produce brilliant metallic glazes:
\[CO_{2(g)}+C_{(s)} \rightleftharpoons 2CO_{(g)} \label{15.3.8}\]
The glaze is created when metal oxides are reduced to metals by the product, carbon monoxide. The equilibrium constant expression for this reaction is as follows:
\[K=\dfrac{[CO]^2}{[CO_2][C]} \label{15.3.9}\]
Because graphite is a solid, however, its molar concentration, determined from its density and molar mass, is essentially constant and has the following value:
\[ [C] =\dfrac{2.26 \cancel{g}/{\cancel{cm^3}}}{12.01\; \cancel{g}/mol} \times 1000 \; \cancel{cm^3}/L = 188 \; mol/L = 188\;M \label{15.3.10}\]
We can rearrange Equation 15.3.8 so that the constant terms are on one side:
\[ K[C]=K(188)=\dfrac{[CO]^2}{[CO_2]} \label{15.3.11}\]
Incorporating the constant value of \([C]\) into the equilibrium equation for the reaction in Equation 15.3.7,
\[K'=\dfrac{[CO]^2}{[CO_2]} \label{15.3.12}\]
The equilibrium constant for this reaction can also be written in terms of the partial pressures of the gases:
\[K_p=\dfrac{(P_{CO})^2}{P_{CO_2}} \label{15.3.13}\]
Incorporating all the constant values into \(K′\) or \(K_p\) allows us to focus on the substances whose concentrations change during the reaction.
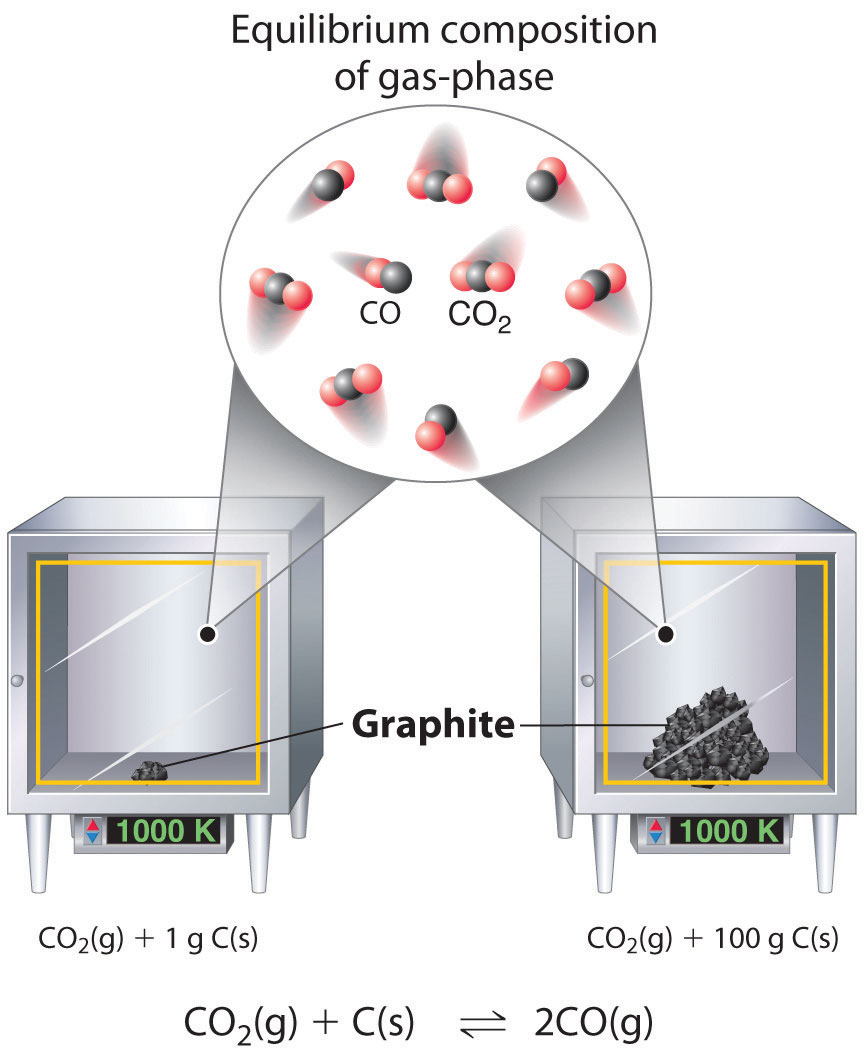
Although the concentrations of pure liquids or solids are not written explicitly in the equilibrium constant expression, these substances must be present in the reaction mixture for chemical equilibrium to occur. Whatever the concentrations of \(CO\) and \(CO_2\), the system described in Equation 15.3.7 will reach chemical equilibrium only if a stoichiometric amount of solid carbon or excess solid carbon has been added so that some is still present once the system has reached equilibrium. As shown in Figure \(\PageIndex{1}\), it does not matter whether 1 g or 100 g of solid carbon is present; in either case, the composition of the gaseous components of the system will be the same at equilibrium.
Write each expression for \(K\), incorporating all constants, and \(K_p\) for the following equilibrium reactions.
- \(PCl_{3(l)}+Cl_{2(g)} \rightleftharpoons PCl_{5(s)}\)
- \(Fe_3O_{4(s)}+4H_{2(g)} \rightleftharpoons 3Fe_{(s)}+4H_2O_{(g)}\)
Given: balanced equilibrium equations
Asked for: expressions for \(K\) and \(K_p\)
Strategy:
Find \(K\) by writing each equilibrium constant expression as the ratio of the concentrations of the products and reactants, each raised to its coefficient in the chemical equation. Then express \(K_p\) as the ratio of the partial pressures of the products and reactants, each also raised to its coefficient in the chemical equation.
Solution
This reaction contains a pure solid (\(PCl_5\)) and a pure liquid (\(PCl_3\)). Their concentrations do not appear in the equilibrium constant expression because they do not change significantly. So
\[K=\dfrac{1}{[Cl_2]}\]
and
\[K_p=\dfrac{1}{P_{Cl_2}}\]
This reaction contains two pure solids (\(Fe_3O_4\) and \(Fe\)), which do not appear in the equilibrium constant expressions. The two gases do, however, appear in the expressions:
\[K=\dfrac{[H_2O]^4}{[H_2]^4}\]
and
\[K_p=\dfrac{(P_{H_2O})^4}{(P_{H_2})^4}\]
Write the expressions for \(K\) and \(K_p\) for the following reactions.
- \(CaCO_{3(s)} \rightleftharpoons CaO_{(s)}+CO_{2(g)}\)
- \( \underset{glucose}{C_6H_{12}O_{6(s)}} + 6O_{2(g)} \rightleftharpoons 6CO_{2(g)}+6H_2O_{(g)}\)
Answer:
- \(K = [CO_2]\) and \(K_p = P_{CO_2}\)
- \(K=\dfrac{[CO_2]^6[H_2O]^6}{[O_2]^6}\) and \(K_p=\dfrac{(P_{CO_2})^6(P_{H_2O})^6}{(P_{O_2})^6}\)
For reactions carried out in solution, the concentration of the solvent is omitted from the equilibrium constant expression even when the solvent appears in the balanced chemical equation for the reaction. The concentration of the solvent is also typically much greater than the concentration of the reactants or products (recall that pure water is about 55.5 M, and pure ethanol is about 17 M). Consequently, the solvent concentration is essentially constant during chemical reactions, and the solvent is therefore treated as a pure liquid. The equilibrium constant expression for a reaction contains only those species whose concentrations could change significantly during the reaction.
The concentrations of pure solids, pure liquids, and solvents are omitted from equilibrium constant expressions because they do not change significantly during reactions when enough is present to reach equilibrium.
Summary
- The law of mass action describes a system at equilibrium in terms of the concentrations of the products and the reactants.
- For a system involving one or more gases, either the molar concentrations of the gases or their partial pressures can be used.
- Definition of equilibrium constant in terms of forward and reverse rate constants: \[K=\dfrac{k_f}{k_r} \]
- Equilibrium constant expression (law of mass action): \[K=\dfrac{[C]^c[D]^d}{[A]^a[B]^b} \]
- Equilibrium constant expression for reactions involving gases using partial pressures: \[K_p=\dfrac{(P_C)^c(P_D)^d}{(P_A)^a(P_B)^b} \label{15.3.1}\]
- Relationship between \(K_p\) and \(K\): \[K_p = K(RT)^{Δn}\]
An equilibrated system that contains products and reactants in a single phase is a homogeneous equilibrium; a system whose reactants, products, or both are in more than one phase is a heterogeneous equilibrium. For gases, the equilibrium constant expression can be written as the ratio of the partial pressures of the products to the partial pressures of the reactants, each raised to a power matching its coefficient in the chemical equation. An equilibrium constant calculated from partial pressures (\(K_p\)) is related to \(K\) by the ideal gas constant (\(R\)), the temperature (\(T\)), and the change in the number of moles of gas during the reaction. An equilibrium system that contains products and reactants in a single phase is a homogeneous equilibrium; a system whose reactants, products, or both are in more than one phase is a heterogeneous equilibrium. When a reaction can be expressed as the sum of two or more reactions, its equilibrium constant is equal to the product of the equilibrium constants for the individual reactions.

