10.1: Bonding Theories
- Page ID
- 37042
As we have talked about using Lewis structures to depict the bonding in organic compounds, we have been very vague in our language about the actual nature of the chemical bonds themselves. We know that a covalent bond involves the ‘sharing’ of a pair of electrons between two atoms - but how does this happen, and how does it lead to the formation of a bond holding the two atoms together?
In this chapter, the valence bond theory is introduced to describe bonding in organic molecules. In this model, bonds are considered to form from the overlapping of two atomic orbitals on different atoms, each orbital containing a single electron. In looking at simple inorganic molecules such as H2 or HF, our present understanding of s and p atomic orbitals will suffice. In order to explain the bonding in organic molecules, however, we will need to introduce the concept of hybrid orbitals.
Valence bond theory is adequate for describing many aspects of organic structure. In some cases, however, chemists need to use a different model, called molecular orbital (MO) theory, to talk about covalent bonds in which electrons are shared not just between two atoms, but between several, or even over an entire molecule.
Example: The H2 molecule
The simplest case to consider is the hydrogen molecule, H2. When we say that the two electrons from each of the hydrogen atoms are shared to form a covalent bond between the two atoms, what we mean in valence bond theory terms is that the two spherical 1s orbitals overlap, allowing the two electrons to form a pair within the two overlapping orbitals.

These two electrons are now attracted to the positive charge of both of the hydrogen nuclei, with the result that they serve as a sort of ‘chemical glue’ holding the two nuclei together.
How far apart are the two nuclei? That is a very important issue to consider. If they are too far apart, their respective 1s orbitals cannot overlap, and thus no covalent bond can form - they are still just two separate hydrogen atoms. As they move closer and closer together, orbital overlap begins to occur, and a bond begins to form. This lowers the potential energy of the system, as new, attractive positive-negative electrostatic interactions become possible between the nucleus of one atom and the electron of the second.
But something else is happening at the same time: as the atoms get closer, the repulsive positive-positive interaction between the two nuclei also begins to increase.
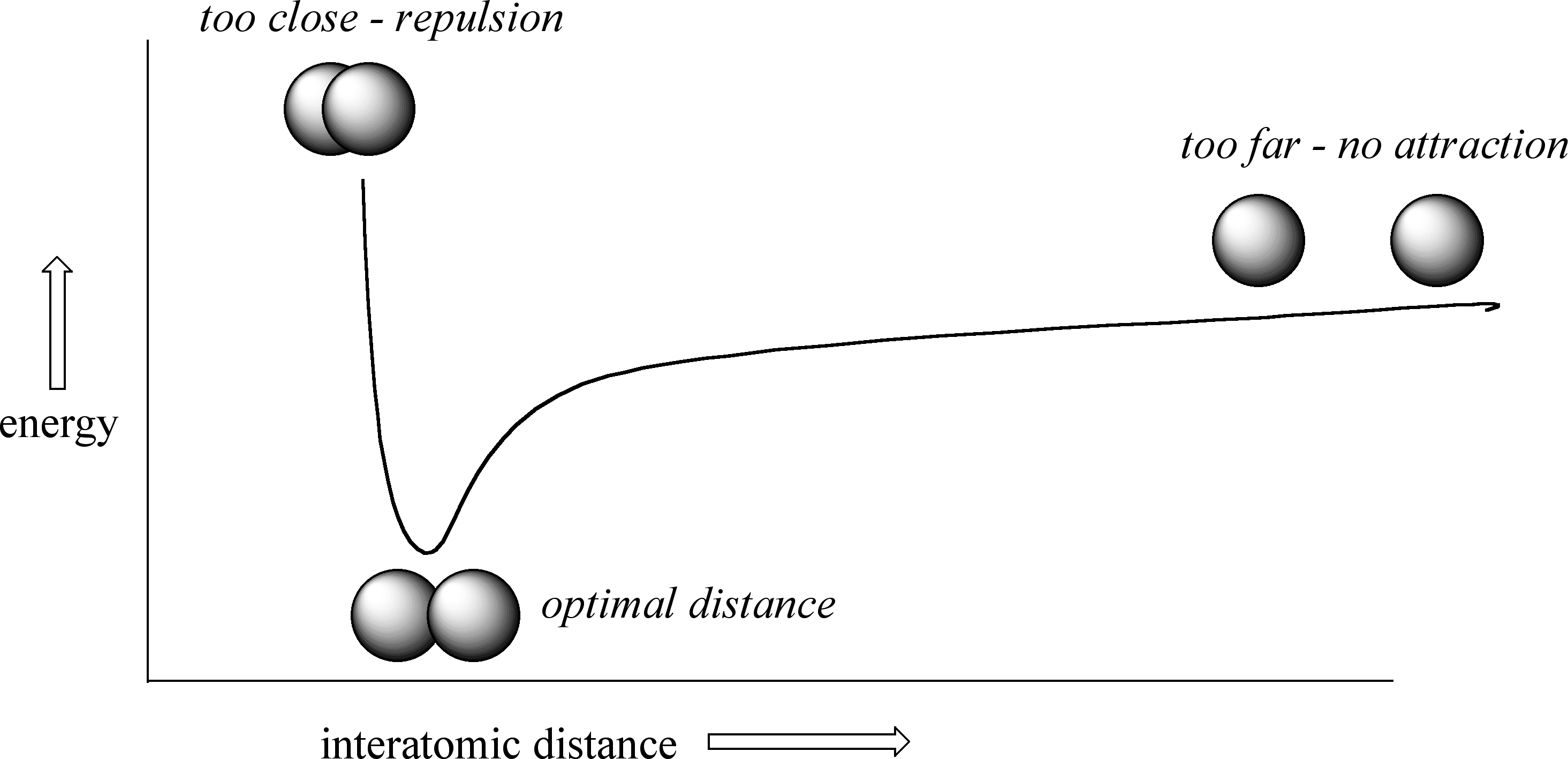
At first this repulsion is more than offset by the attraction between nuclei and electrons, but at a certain point, as the nuclei get even closer, the repulsive forces begin to overcome the attractive forces, and the potential energy of the system rises quickly. When the two nuclei are ‘too close’, we have a very unstable, high-energy situation. There is a defined optimal distance between the nuclei in which the potential energy is at a minimum, meaning that the combined attractive and repulsive forces add up to the greatest overall attractive force. This optimal internuclear distance is the bond length. For the H2 molecule, this distance is 74 x 10-12 meters, or 0.74 Å (Å means angstrom, or 10-10 meters). Likewise, the difference in potential energy between the lowest state (at the optimal internuclear distance) and the state where the two atoms are completely separated is called the bond energy. For the hydrogen molecule, this energy is equal to about 104 kcal/mol.
Every covalent bond in a given molecule has a characteristic length and strength. In general, carbon-carbon single bonds are about 1.5 Å long (Å means angstrom, or 10-10 meters) while carbon-carbon double bonds are about 1.3 Å, carbon-oxygen double bonds are about 1.2 Å, and carbon-hydrogen bonds are in the range of 1.0 – 1.1 Å. Most covalent bonds in organic molecules range in strength from just under 100 kcal/mole (for a carbon-hydrogen bond in ethane, for example) up to nearly 200 kcal/mole. You can refer to tables in reference books such as the CRC Handbook of Chemistry and Physics for extensive lists of bond lengths, strengths, and many other data for specific organic compounds.
It is not accurate, however, to picture covalent bonds as rigid sticks of unchanging length - rather, it is better to picture them as springs which have a defined length when relaxed, but which can be compressed, extended, and bent. This ‘springy’ picture of covalent bonds will become very important, when we study the analytical technique known as infrared (IR) spectroscopy.

