5: Intermolecular Forces and Interactions (Worksheet)
- Last updated
- Save as PDF
- Page ID
- 96703
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.
Learning Objectives
- Know the kinds and relative strengths of intermolecular attractive interactions
- Understand the concept of polarizability
- Understand the effects of strengths of intermolecular forces on phase changes and substance properties such as viscosity and surface tension
- Understand the concepts of critical pressure, critical temperature, vapor pressure, normal boiling point, normal melting point, critical point, and triple point
- Understand the processes by which solutions form
- Understand the roles of enthalpy and entropy in determining solubility
- Understand the solubility of non-reactive gases
- Understand the effect of solute concentration on colligative properties
Most substances can exist in either gas, liquid, or solid phase under appropriate conditions of temperature and pressure. The phase that we see under ordinary conditions (room temperature and normal atmospheric pressure) is a result of the forces of attraction between molecules or ions comprising the substance. The strength of these attractions also determines what changes in temperature and pressure are needed to effect a phase transition.
The behavior of a pure substance in any of its phases is altered when it is mixed with other substances to make solutions. Solutions are homogeneous mixtures, which can occur in any phase. But most often in chemistry we are dealing with solutions that are in the liquid phase. An understanding of the processes by which solutions form and of how their properties differ from their pure-substance components is useful in many real-life applications of materials.
Success Criteria
- Be able to judge relative strengths of intermolecular forces of attraction and their effects on properties for a series of compounds
- Be able to interpret heating curves and calculate quantities related to temperature and enthalpies of phase changes
- Be able to interpret and sketch phase diagrams
- Be able to identify the forces responsible for solubility in particular solutions
- Be able to predict solubility, based on the intermolecular forces of the components
- Be able to do Henry’s law calculations of gas solubility
- Be able to calculate molality
- Be able to calculate the magnitude of colligative changes in vapor pressure, freezing point, boiling point, and osmotic pressure
Intermolecular Forces
The tendency of a substance to be found in one state or the other under certain conditions is largely a result of the forces of attraction that exist between the particles comprising it. We will concentrate on the forces between molecules in molecular substances, which are called intermolecular forces. (Forces that exist within molecules, such as chemical bonds, are called intramolecular forces.) The greater the strength of the intermolecular forces, the more likely the substance is to be found in a condensed state; i.e., either a liquid or solid. As we have seen, the model of an ideal gas assumes that the gas particles (molecules or atoms) have virtually no forces of attraction between them, are widely separated, and are constantly moving with high velocity and kinetic energy. In truth, there are forces of attraction between the particles, but in a gas the kinetic energy is so high that these cannot effectively bring the particles together. With stronger intermolecular forces or lower kinetic energy, those forces may draw molecules closer together, resulting in a condensed phase. Going from gas to liquid to solid, molecular velocities and particle separations diminish progressively as structural order increases. In the case of liquids, molecular attractions give rise to viscosity, a resistance to flow. Also, the absence of intermolecular forces above the surface of a liquid results in surface tension, the development of a “skin” on the surface, which causes beading of liquid droplets and also allows light objects to rest on a liquid surface without sinking (e.g., water bugs). Solids have stronger intermolecular forces, making them rigid, with essentially no tendency to flow. Although the mix of types and strengths of intermolecular forces determines the state of a substance under certain conditions, in general most substances can be found in any of the three states under appropriate conditions of temperature and pressure. Changing those conditions can induce a change in the state of the substance, called a phase transition.
Q1
Is the average kinetic energy of molecules greater or lesser than the energy of intermolecular forces of attraction in (a) solids, (b) liquids, and (c) gases?
Q2
Why does increasing the temperature cause a substance to change in succession from a solid to a liquid to a gas?
Q3
Why do substances with high surface tension also tend to have high viscosities?
Q4
Why do surface tension and viscosity decrease with increasing temperature?
Kinds of Intermolecular Forces
We will consider the following types of intermolecular forces: London dispersion, dipole-dipole, and hydrogen bonding. London dispersion forces and dipole-dipole forces are collectively known as van der Waals forces. Molecules can have any mix of these three kinds of intermolecular forces, but all substances at least have London dispersion forces.
London dispersion forces exist for all substances, whether composed of polar or nonpolar molecules. They arise from the formation of temporary, instantaneous polarities across a molecule from circulations of electrons. An instantaneous polarity in one molecule may induce an opposing polarity in an adjacent molecule, resulting in a series of attractive forces among neighboring molecules.
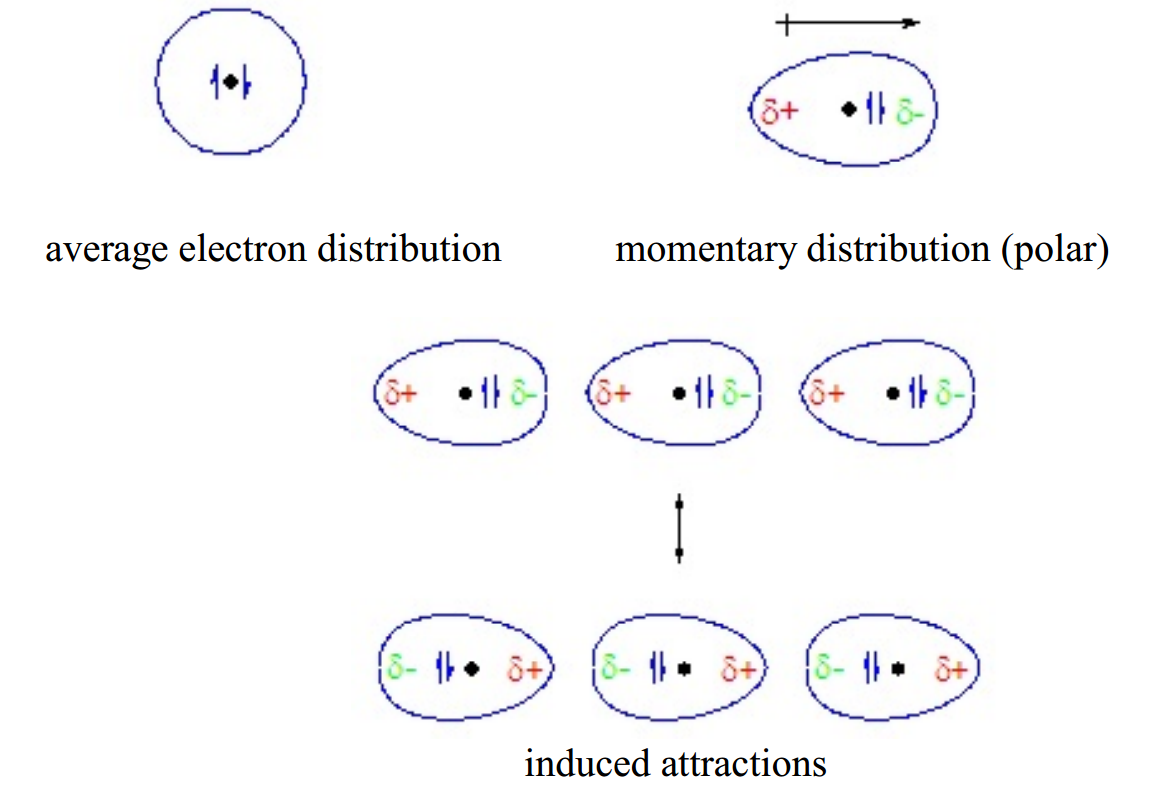
London dispersion forces arise from changing electron distributions. Because all molecules have electrons, all molecular substances have London dispersion forces, regardless of whether they are polar or non-polar. Molecules with higher molecular weights have more electrons, which are generally more loosely held. This makes their electron clouds more deformable from nearby charges, a characteristic called polarizability. As a result, substances with higher molecular weights have higher London dispersion forces and consequently tend to have higher melting points, boiling points, and enthalpies of vaporization. The following data for the diatomic halogens nicely illustrate these trends.
| Element | F2 | Cl2 | Br2 | I2 |
|---|---|---|---|---|
| m.p. (°C) | -220 | -101 | -7.3 | 114 |
| b.p. (°C) | -188 | -34 | 58.8 | 184 |
| At 25 °C | gas | gas | liquid | solid |
Dipole-dipole forces of attraction exist between molecules that are polar – those that have a permanent dipole moment. The polarities of individual molecules tend to align by opposites, drawing the molecules together and thereby favoring a condensed phase.
.png?revision=1&size=bestfit&width=459&height=290)
These additional forces of attraction must be overcome in a transition to a less-ordered phase (e.g., solid to liquid, liquid to gas), so substances with dipole-dipole attractions between their molecules tend to have higher melting points and boiling points than comparable compounds composed of nonpolar molecules, which only have London dispersion intermolecular forces.
A hydrogen bond is a non-covalent attraction between a hydrogen that is covalently bonded to a very electronegative atom (X) and another very electronegative atom (Y), most often on an adjacent molecule. (X and Y may be the same or different elements.)
.png?revision=1&size=bestfit&width=384&height=111)
For the most part, only compounds in which hydrogen is covalently bonded to O, N, or F are candidates for hydrogen bonding. Covalent bonds with these elements are very polar, resulting in a partial negative charge (δ–) on the O, N, or F. This partial negative charge can be attracted to the partial positive charge (δ+) of the hydrogen in an X–H bond on an adjacent molecule. Thus, the H×××Y hydrogen bond, unlike the covalent X–H bond, results mainly from electrostatic attraction. Hydrogen bond strengths typically are in the range 4 - 46 kJ/mol, much less than the strengths of typical covalent bonds. Nonetheless, hydrogen bond strength is significantly greater than either London dispersion forces or dipole-dipole forces. Hydrogen bonds in HF(s) and H2O(s) (shown on the next page) are intermediate in strength within this range.
.png?revision=1&size=bestfit&width=640&height=225)
Nonpolar molecules only have London dispersion forces, which tend to be the weakest of the three kinds of intermolecular forces. Polar molecules add another kind of force, beyond their London forces, and so have stronger overall intermolecular forces of attraction. If a molecule is capable of hydrogen bonding, then it has all three kinds of intermolecular forces and has the strongest overall mix. As the kinds of intermolecular forces increase, substances have a greater tendency to exist in a condensed phase, have higher melting points and boiling points, and as liquids have lower vapor pressure and higher viscosity.
Q5
Name the kind or kinds of intermolecular forces that must be overcome to convert the following from liquid or solid to gas: (a) \(Br_2\), (b) \(CH_3OH\), (c) \(CO_2\), (d) \(HCN\), (e) \(NH_3\)
Q6
Normal alkanes are hydrocarbons with unbranched carbon chains, having a general formula \(C_nH_{2n+2}\). At room temperature, ethane, \(C_2H_6\), is a gas; hexane, \(C_6H_{14}\), is a liquid; and Octadecane, \(C_{18}H_{38}\), is a solid. Describe the intermolecular forces present in each substance and explain the differences in their room-temperature phases.
Q7
Arrange the following in order of increasing boiling point:

Heating Curves
As we continuously heat a solid substance, such as ice, over time it can pass through all phases, giving a behavior represented by the following heating curve.
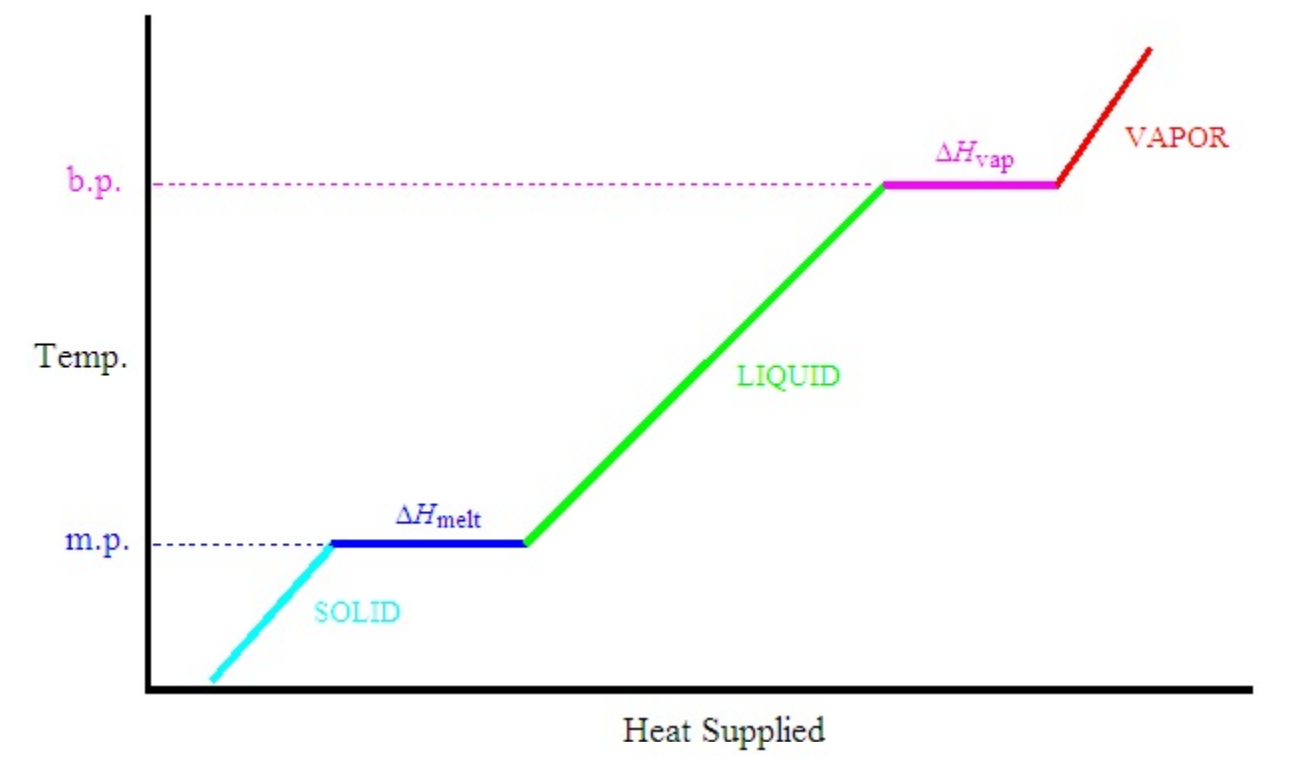
For a given input of heat, q, the temperature rises by different amounts in the solid, liquid, and vapor phases due to the different heat capacities for each phase. In a single phase, ΔT = q/C, where C is the heat capacity for the phase in the range of the temperature change. Put another way, in a single phase the amount of heat that must be added to raise the temperature a certain amount, ΔT, is given by q = C ΔT. At both the melting point and boiling point, the temperature remains constant with heat input so long as both phases involved with the transition exist. At these points, all the heat is used to effect the conversion of one phase into another (from solid to liquid at the melting point or from liquid to vapor at the boiling point). Once conversion is complete, the temperature of the substance will rise with addition of heat. At the melting point, the amount of heat required to convert one mole of substance from solid to liquid defines the molar heat of fusion, ΔHfus, also called the molar heat of melting, ΔHmelt. At the boiling point, the amount of heat required to convert one mole of substance from liquid to vapor is called the molar heat of vaporization, ΔHvap.
Q8
How much heat is required to heat 10.0 g of ice at -5.00 °C to become liquid water at +7.00 °C? In this temperature range, the heat capacity of H2O(s) is 37.7 J/mol×K, and the heat capacity of H2O(l) is 75.8 J/mol×K. The molar heat of fusion of ice is 6.01 kJ/mol.
Vapor Pressure
If a liquid is placed in a closed container, both evaporation and condensation will occur simultaneously. Initially, evaporation predominates, because there are so few molecules in the vapor phase above the liquid. As more and more molecules build up in the vapor, some will strike the liquid surface, be attracted to liquid molecules, and rejoin the liquid phase. At some point the rate of molecules escaping the liquid will equal the rate of molecules rejoining it from the vapor. This marks the onset of a state of dynamic equilibrium at which the rates of evaporation and condensation are equal. At this point, the number of vapor molecules in the volume above the liquid remains constant over time. The resulting partial pressure of the vapor in equilibrium with the liquid is the vapor pressure. The vapor pressure depends upon the nature of the liquid (ΔHvap), the kinetic energy of the molecules (increasing with temperature), and the resulting vapor concentration.
Although different substances may have different vapor pressures at the same temperature (higher for more volatile substances), all vapor pressures increase with increasing temperature. When the temperature is high enough that a liquid’s vapor pressure equals the ambient pressure, boiling will commence. At temperatures where the vapor pressure is lower than the ambient pressure, no bubbles of vapor can form in the liquid, because the greater air pressure would cause them to collapse. The higher the ambient pressure, the higher the boiling point will be. For this reason, we define the normal boiling point at 1 atm. Conversely, boiling occurs at a lower temperature when the ambient pressure is lower. For example, Mt. Washington (elevation 6288 ft) has a typical air pressure of 610 torr. At 94 °C, the vapor pressure of water is 610.90 torr, so this is approximately the boiling point of water atop Mt. Washington. Consequently, foods tend to require longer cooking times at high altitudes.
Q9
Explain how each of the following affects the vapor pressure of a liquid: (a) the volume of the liquid, (b) the volume of the container, (c) the surface area of the liquid, (d) the temperature, (e) intermolecular forces of attraction, (f) the density of the liquid.
Phase Diagrams
The relationships between temperature and pressure and the phase transitions of a substance can be summarized in a phase diagram. The phase diagram for carbon dioxide is shown below.
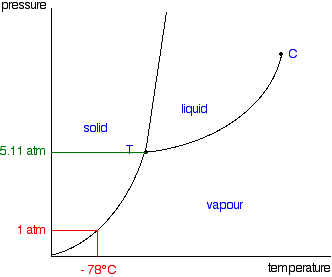
For any combination of temperature and pressure that falls entirely within a phase region, only that one phase will exist. Lines on the diagram represent combinations of temperature and pressure under which two phases coexist (e.g., gas-liquid, liquid-solid, solid-gas). The triple point (T) is the combination of temperature and pressure at which all three phases are simultaneously in equilibrium. The critical point (C) marks the limit on the ability to condense a vapor with applied pressure at high temperature. Above this point it is not possible to condense the gas regardless of increasing pressure. The critical temperature, Tc, is the point above which a gas cannot be liquefied, regardless of the pressure. The critical pressure, Pc, is the minimum pressure needed to cause condensation at the critical temperature. Above the critical point the substance exists as a supercritical fluid.
Q10
Describe the phases and/or phase transitions experienced by CO2 under the following conditions:
- Heating from –100 °C to 30 °C at 1.0 atm
- Heating from –100 °C to 50 °C at 70 atm
- A sample at 35 °C and 100 atm
- A sample at –50 °C and 6.0 atm
Q11
Does carbon dioxide have a normal boiling point? Explain.
Q12
Describe the conditions under which liquid carbon dioxide boils.
The Solution Process
A solute dissolves in a solvent because the attractive forces between solvent and solute particles (i.e., ions and/or molecules) are similar to those between the solute particles themselves. As a rule: "Like dissolves like." When two substances have dissimilar intermolecular forces of attraction, their molecules tend to be more attracted to themselves and remain in the pure, unmixed state. In such cases, the solute is said to be insoluble in the solvent. But the term “insoluble” is relative. Most solutes have some (albeit limited) solubility in a given solvent. Thus, "insoluble" usually means "negligibly soluble" or "sparingly soluble".
Any of the intermolecular forces we have previously discussed can occur between solute and solvent molecules, resulting in solution formation. London dispersion forces, dipole-dipole attractions, or hydrogen bonding between solute and solvent molecules can induce the solute molecules to break away from the attractions they have with their own molecules to enter the solution. This process is called solvation in general, but when water is the solvent it is called hydration. In aqueous solutions the solute molecules or ions are surrounded by waters of hydration, which prevent their recombination.
When an ionic crystal dissolves in water, it dissociates to form hydrated ions, which are cations and anions surrounded by water molecules; e.g.,
\[NaCl(s) + xH_2O \rightarrow [Na(H_2O)_n]^+ + [Cl(H_2O)_m]^– \nonumber \]
In this case, ion-dipole attractions and the stability of the resulting hydrated ions overcome the Coulombic attractions between the ions in the crystal lattice. The ions in solution are prevented from recombining because the surrounding waters of hydration do not allow them to get close enough together.
Some molecules with highly polar bonds, such as the binary acids, \(HX\), may dissolve in water partially or completely as ions. The process is similar to the dissolving of ionic solutes, but in this case it is the strength of the covalent bonds within the solute molecules that must be overcome; e.g.,
\[HCl(g) + H_2O \rightarrow H_3O^+(aq) + Cl^–(aq) \nonumber \]
The attraction between solvent water molecules and the solute molecules is initially dipole-dipole, but the attraction between the dissociated ions and the their waters of hydration is ion-dipole. These ion-dipole attractions interfere with recombination to form undissociated molecules.
If the intermolecular forces in the solute and solvent are very different, the solute will have little or no appreciable solubility. For example, a nonpolar liquid like benzene, C6H6, which only has London dispersion forces between its molecules, has poor solubility in water, which is a polar solvent with hydrogen bonding. Likewise, benzene is a poor solvent for ionic substances, such as NaCl, because it is incapable of establishing the necessary ion-dipole attractions that keep ions in solution.
Q13
Identify the principal type of solute-solvent interaction that is responsible for forming the following solutions:
- KNO3 in water
- Br2 in benzene, C6H6
- glycerol, CH2(OH)CH(OH)CH2OH, in water
- HCl in acetonitrile, CH3CN [HCl does not form ions in CH3CN]
Q14
For the following carboxylic acids, predict whether solubility will be greater in water or carbon tetrachloride, and give your reasoning: (a) acetic acid, CH3CO2H, (b) stearic acid, CH3(CH2)16CO2H.
Enthalpy and Entropy of Solution
When a solute dissolves in a solvent the enthalpy of the overall process, expressed as ΔHsoln, may be exothermic or endothermic; e.g.,
\[CaCl_2(s) \rightarrow Ca^{2+}(aq) + 2Cl^–(aq) + \text{heat} \nonumber \]
with \(ΔH_{soln} < 0\) (exothermic)
\[\text{heat} + KNO_3(s) \rightarrow K^+(aq) + NO_3^–(aq) \nonumber \]
with \(ΔH_{soln} > 0\) (endothermic)
The enthalpy of solution can be analyzed as the sum of the following processes:
- Enthalpy to overcome attractions between solute molecules (\(ΔH_1 > 0\) (an endothermic process))
- Enthalpy to overcome attractions between solvent molecules (\(ΔH_2 > 0\) (an endothermic process))
- Enthalpy to form solvated molecules through solute-solvent attractions. (\(ΔH_3 < 0\) (an exothermic process)
The overall enthalpy of solution is
\[ΔH_{soln} = ΔH_1 + ΔH_2 + ΔH_3. \nonumber \]
If
\[|ΔH_3| > (ΔH_1 + ΔH_2), \nonumber \]
then \(ΔH_{soln} < 0\) and the dissolving process is exothermic.
If
\[|ΔH_3| < (ΔH_1 + ΔH_2), \nonumber \]
then \(ΔH_{soln} > 0\) and the dissolving process is endothermic.
If a solute is soluble in a solvent, the overall process is said to be spontaneous. If a solute does not dissolve in a solvent (insoluble) the solution process is said to be non-spontaneous. A spontaneous process or change proceeds in a given direction without needing to be driven by an external energy input. As we have seen repeatedly, reactions or processes that are exothermic, in which the energy content of the system goes down, tend to be spontaneous (e.g., combustion). But some endothermic reactions or processes are also spontaneous. As just noted, both CaCl2 and KNO3 dissolve spontaneously in water. CaCl2 does so exothermically, but KNO3 does so endothermically. In both cases, the solution process disperses the ions from their highly ordered crystal lattice into the a much more disordered state in solution. The degree of disorder in a system is associated with the thermodynamic function called entropy (about which we will have much more to say later). When a solute dissolves in a solvent, the dispersal of the solute particles results in an increase in entropy, which favors a spontaneous solution process. In the case of solutes like KNO3 the entropy factor favoring spontaneity is greater than the enthalpy factor favoring non-spontaneity, and dissolving is spontaneous. The process is said to be entropy controlled. If the increase in entropy is not great enough, an endothermic process will be non-spontaneous and is said to be enthalpy controlled. The heat of solution of an insoluble solute is usually endothermic, with too small an entropy increase to make the overall process spontaneous.
Q15: An Ideal Solution
Hexane (C6H14) and heptane (C7H16) are miscible in all proportions with \(ΔH_{soln} \gg 0\).
- Why are these two liquids miscible with each other?
- Why is \(ΔH_{soln} \gg 0\) for this pair of liquids?
- Why do they spontaneously form solutions, given that \(ΔH_{soln} \gg 0\)?
Solubility of Non-reactive Gases
When non-reactive gases dissolve in a solvent, both pressure and temperature significantly affect solubility. Most non-reactive gases have very small solubilities, which increase with increasing partial pressure of the dissolving gas. At a given temperature and with moderate partial pressures (\(\le atm\)), many non-reactive gases obey Henry's Law:
\[P_g = K\chi_g \nonumber \]
where \(P_g\) is the partial pressure of the gas over the solution, \(K\) is a constant for the particular gas and solvent at the given temperature, and \(\chi_g\) is the mole fraction of the gas in the solution. At the low concentrations typical of dissolved non-reactive gases, mole fraction is proportional to concentration in the usual units, such as mol/L or g/L. Therefore, Henry's Law can be restated as
\[C_g = k P_g \nonumber \]
where Cg is the concentration of the dissolved gas, and \(k\) is the Henry's Law constant for the particular gas and solvent pair, expressed in appropriate concentration units per unit pressure, usually in atm. Gas solubility is always less at higher temperature (i.e., \(k\) is smaller).
Q16
The solubility of \(N_2\) at p(N2) = 1 atm is 1.75 x 10-3 g/100 mL of water. What is the solubility in water at an air pressure of 2.51 atm, the pressure at 50 ft below the surface of the water? Air is 78.1 vol-% N2. [Hint: What is the partial pressure of N2(g) when the air pressure is 2.51 atm?]
Molality and Colligative Properties
The presence of solute molecules changes certain properties in the solution from what they are in the pure solvent. Solution properties such as these, which are dependent on concentration, are called colligative properties. Examples of colligative properties include vapor pressure, boiling point, freezing point, and osmotic pressure. For discussions of colligative properties it is often convenient to express solution concentration in terms of molality:
\[ \text{molality} = m = \dfrac{\text{moles of solute}}{\text{kg of solvent}} \nonumber \]
The magnitude of any colligative effect depends on the total concentration of solute particles in the solution, not on the number of moles of solute added to make up the solution.
In short, you have to ask yourself “What are the concentrations of all solute particles in this solution?” For a strong electrolyte at moderate concentration, we can assume that all of the ionic solid has broken up into its 3 4 component ions on dissolving. For example, a 0.100 m solution of K PO has four times the concentration of solute particles as a 0.100 m solution of sugar, because each formula unit of \(K_3PO_4\) breaks up on dissolving into three K ions and one \(PO_4^{3-}\) ion:
\[ K_3 PO_4 (s) \rightarrow 3 K^+ (aq) + PO_4^{3-}(aq) \nonumber \]
In other words, the molality of \(K^+\) ions is (3)(0.100 m) = 0.300 m, the molality of \(PO_4^{3-}\) ions is (1)(0.100 m), and the total molality for all ions is 0.300 m + 0.100 m = 0.400 m. It is the total concentration of ions that causes the change in solution properties. If calculating a colligative effect on the basis of molality, we would use 0.400 m for such a solution of \(K_3PO_4\), rather than 0.100 m, as we would for a sugar solution.
Q17
Calculate the molality of ethanol, \(C_2H_5OH\) (m.w. = 46.06) in a solution prepared by dissolving 5.00 g of ethanol in 25.00 g of water.
Q18
Calculate the total molality of all ions in a solution prepared by dissolving 20.0 g of \((NH_4)_2SO_4\) in 95.0 g of water. [f.w. (NH ) SO = 132 u]
Vapor Pressure above Solutions with Nonvolatile Solutes
If we add a nonvolatile solute (one that doesn’t have a vapor pressure of its own) to a volatile solvent, the solute particles (molecules, ions, or mixture of both) will block the escape of the solvent molecules into the vapor. This will reduce the vapor pressure over the solution, compared to what it would be if the solvent had nothing dissolved in it. The solvent’s vapor pressure above such a solution is reasonably well predicted by a special case of Raoult's Law:
\[P_{soln} = \chi_{solv} P^o_{solv} \nonumber \]
where \(P_{soln}\) is the vapor pressure above the solution at equilibrium, \(\chi_{solv}\) is the mole fraction of the solv solvent (not the solute) in the solution, and \( P^o_{solv}\) is the vapor pressure the pure solvent would have at the temperature of the solution.
Q19
Consider a 2.00 m solution of sugar in water at 25 °C.
- What is the value of the mole fraction of water in this solution? [Hint: Imagine that the 2 solution was made up with exactly 1 Kg of water.] (m.w. H O = 18.02 u)
- Calculate the vapor pressure above a 2.00 m solution of sugar in water at 25 °C, given that the vapor pressure of pure water at this temperature is 23.76 mm Hg.
Q20
Calculate the 2 4 expected vapor pressure above a 2.00 m solution of \(Na_2SO_4\) in water at 25.00 C. Compare this result to what you found in part a of the preceding
Vapor Pressure above Solutions of Volatile Components
If a solution is made of two or more volatile components, the total vapor pressure above the solution should be the sum of the vapor pressures (partial pressures) arising from each of the components in the mixture, as predicted by Dalton's Law of Partial Pressures. If the component liquids do not interact with each other appreciably, they are said to form an ideal solution. In this case the partial vapor pressure above the solution from each component liquid is given by
\[P_{i} = \chi_{i}^{soln} P^o_{i} \nonumber \]
where \(P_i\) is the vapor pressure from an individual component, \(\chi_{i}^{soln}\) is the mole fraction of the solution component in the solution, and \(P^o_{i}\) is the vapor pressure the pure liquid would have at the given temperature. Thus, the general form of Raoult's Law with \(n\) components can be stated as
\[P_t = \sum_i^n \chi_{i}^{soln} P^o_{i} = \chi_{1}^{soln} P^o_{1} +\chi_{2}^{soln} P^o_{2} + \dots \chi_{n}^{soln} P^o_{n} \label{expand} \]
For a two-component system, Equation \ref{expand} is
\[P_t = \chi_{1}^{soln} P^o_{1} +\chi_{2}^{soln} P^o_{2} \nonumber \]
this equation can be further simplified with the relationship that
\[ \chi_{1}^{soln} + \chi_{1}^{soln} =1 \nonumber \]
It should be emphasized that Raoult's Law applies to ideal solutions, in which interactions between solvent and solute molecules are virtually identical to those in the neat liquids. No real solution shows this behavior over a significant range of concentrations. A few carefully chosen mixtures, particularly with one component in very small mole fraction, approximate Raoult's Law.
The composition of the vapor above a mixture of two or more volatile liquids is not the same as in the solution. In general, more volatile components (as indicated by their higher vapor pressure as a neat liquid) will have a higher mole fraction in the vapor than in the solution. From Dalton’s Law of Partial Pressures, the mole fraction of a component in the vapor mixture is its partial pressure divided by the total pressure; i.e., \(\chi_i^{vap} = P_i/P_t\).
Q21
What are the partial pressures and total vapor pressure above a solution at 20 °C made by mixing 12.5 g benzene (\(C_6H_6\)) with 44.2 g toluene (\(C_6H_5CH_3\)). At 20 °C, \(P^o (C_6H_6) = 74.7\, torr\) and \(P^o (C_6H_5CH_3) = 22.3\, torr\). [m.w. benzene and toluene is 78.11 and 92.14, respectively).
Q22
In terms of mole fractions, what is the composition of the vapor above the previously described benzene-toluene mixture?
Boiling Point Elevation and Freezing Point Depression
The presence of nonvolatile solute particles in solution interferes with the solvent molecules’ escape from the liquid phase. This is the cause of the vapor pressure lowering. This also means that a higher temperature must be used to achieve a vapor pressure of 1 atm, which defines the normal boiling point. Thus, a solution of a nonvolatile solute and a volatile solvent has a higher boiling point (boiling point elevation). Similarly, solute particles interfere with the formation of the solid on cooling, so freezing occurs at a lower temperature (freezing point depression). The temperature shift due to boiling point elevation or freezing point depression can be calculated by the formula
\[\Delta T = Km \nonumber \]
where \(K\) is either the boiling point elevation constant (\(K_b\)) or the freezing point depression constant (\(K_f\)). The two constants have different values for a particular liquid, and K is generally a bigger number. Don’t worry about the sign on the ÄT. Just know that the value must be added to the normal boiling point and subtracted from the normal freezing point of the pure solvent.
Boiling point elevations and freezing point depressions can be used to determine molecular weights of solutes. Because \( K_f > K_b\) for a given solvent and boiling points are sensitive to pressure conditions, freezing point depression (or, equivalently, melting point depression) is generally the preferred method. This is called cryoscopic molecular weight determination. A weighed amount of substance whose molar mass is to be determined (the unknown) is dissolved in a known mass of solvent, and the new freezing point (or melting point) of the mixture is observed to determine \(\Delta T_b\). Using this and the solvent’s \(K_b\) value, the molality of the solution is calculated. With this known number of moles of solute per kilogram of solvent (molality) and the mass composition of the solution as it was made up, it is possible to calculate the solute’s number of grams per mole (its molar mass).
Q23
Pure benzene has a freezing point of 5.5 °C and a boiling point of 80.1 °C. What are the o o expected freezing point and boiling point for a 0.15 m solution of a nonvolatile solute in benzene? f b For benzene, \(K_f = 5.12 °C/m\) and \(K_b = 2.53 °C/m\).
Q24
When 45.0 g of an unknown nonvolatile nonelectrolyte is dissolved in 500.0 g of water, the resulting solution freezes at -0.930 °C. What is the molar mass of the unknown substance? \(K_f = 1.86 °C/m\) for water.
Osmotic Pressure
Osmotic pressure is associated with the situation in which a solution and the pure solvent (or a more dilute solution) are separated by a semipermeable membrane, which has pores only big enough to allow solvent molecules to pass through, but not solute molecules. Because the concentration of solvent molecules is greater on the pure solvent side, more solvent molecules on that side will strike the membrane, hit a hole, and pass through. This results in net flow of solvent from the pure solvent side to the solution side, resulting in dilution over time. Many tissues in living organisms serve as semipermeable membranes, and osmotic pressure is very important in understanding physiology.
In 1887 Jacobus van 't Hoff discovered that the flow could be stopped or even reversed by applying pressure to the solution side. The necessary minimum pressure to stop the diffusion of solvent into the solution is called the osmotic pressure, \(\Pi\), given by
\[\Pi = MRT \label{osmotic} \]
where \(M\) is the molarity of the solution, \(T\) is temperature in Kelvin, and \(R\) is the gas constant, \(0.08206\, L \,atm/(K mol)\). If a pressure greater than \(\Pi\) is applied, reverse osmosis will occur, reducing the amount of solvent on the solution side as it is transferred to the pure solvent side. This is used as one way of purifying drinking water. Notice that Equation \ref{osmotic} resembles the ideal gas law \[PV=nRT \nonumber \] written with the definition of molarity \(M= n/V\)
Q25
What is the osmotic pressure of a 0.100 M glucose solution in torr at 25.0 °C?
Q26
Sea water is approximately 0.60 M \(NaCl\). What is the minimum applied pressure that must be exceeded to achieve water purification by reverse osmosis at 25 °C?


