5.6: Larmour Frequency

When placed in a magnetic field, charged particles will precess about the magnetic field. In NMR, the charged nucleus, will then exhibit precessional motion at a characteristic frequency known as the Larmor Frequency. The Larmor frequency is specific to each nucleus and is measured during the NMR experiment, as it is dependent on the magnetic field that the nucleus experiences.

Precessing Tops

Apply an external magnetic field, \(\vec{H}_o\) that defines a direction in space (e.g., z). Assume that \(\vec{H}_o\) makes an angle, \(θ\), with \(\vec{\mu}\), so that we have:

\[\begin{aligned}
\mu &=|\mu| \cos \theta \\[4pt]
\mu_{\perp} &=|\mu| \sin \theta
\end{aligned} \]

The applied magnetic field exerts a torque, \(\vec{\tau}\) on the nucleus that is given by the cross product:

\[\begin{aligned} \vec{\tau}&=\vec{\mu} \times \vec{H}_{\circ} \\[4pt]&=|\mu||H| \sin \theta \\[4pt]&=H \mu_{\perp} \end{aligned} \]

The direction of \(\vec{\tau}\) is perpendicular to the plane formed by \(\vec{\mu}\) and \(\vec{H}_o\). Thus, as shown in Figure \(\PageIndex{1}\), this torque cause to process about the direction of \(\vec{H}_o\). The tip sweeps out a cone and \(\vec{\tau}\) is an angular force on the spinning nucleus causing it to wobble, just like a gyroscope wobbles in a gravitational field aka a spinning top.

Figure \(\PageIndex{1}\): The wobbling of a spinning nucleus.

The torque is the time derivative of the angular momentum. This is the angular analog of the linear relationships you know in basic physics classes, where the force is the derivative of the linear momentum:

\[\frac{d}{d t} \vec{p}=\frac{d}{d t} m \vec{v}=m \frac{d}{d t} \vec{v}=m \vec{a}=\vec{F} \nonumber \]

For angular systems

\[\frac{d}{d t} \vec{J}=\hbar \frac{d}{d t} \vec{I}=\vec{\tau}=\vec{\mu} \times \vec{H}_{\circ} \nonumber \]

Multiplying by \(\gamma\) gives

\[\frac{d}{d t} \gamma \vec{J}=\frac{d}{d t} \vec{\mu}=\gamma\left(\vec{\mu} \times \vec{H}_{\circ}\right) \nonumber \]

Set of three linear differential equations relating the components of \(\vec{mu}\). This can be rewritten

\[\dot{\vec{\mu}}=-\gamma\left(H_{\circ} \times \vec{\mu}\right) \nonumber \]

(sign change due to flipping the cross product)

\[\left(\begin{array}{c}
\dot{\vec{\mu}}_{x} \\
\dot{\vec{\mu}}_{y} \\
\dot{\vec{\mu}}_{z}
\end{array}\right)=-\gamma\left(\begin{array}{ccc}
\vec{i} & \vec{j} & \vec{k} \\
0 & 0 & H_{\circ} \\
\mu_{x} & \mu_{y} & \mu_{z}
\end{array}\right) \nonumber \]

This results from the determent form of the cross product

\[\dot{\vec{\mu}}=-\gamma\left(-\vec{i}\left(H_{\circ} \mu_{y}\right)-\vec{j}\left(H_{\circ} \mu_{x}\right)+\vec{k}(0)\right) \nonumber \]

Note that \(\vec{\mu}_{z}=0\). This means that \(θ\) is constant defining \(\mu\) and \(\mu_{\perp}\) from the initial conditions. A solution to this set of equations:

\[\begin{gathered}
\frac{d \mu_{x}}{d t}=\gamma H_{\circ} \mu_{y} \\
\frac{d \mu_{y}}{d t}=-\gamma H_{\circ} \mu_{x} \\
\frac{d \mu_{z}}{d t}=0
\end{gathered} \nonumber \]

where \(\mu\) is the magnitude of \(\vec{\mu}\). The equations above represent a rotation of \(\mu_{\perp}\) in the xy-plane with angular frequency \(\omega_{0}\). Same as the precession of \(\vec{\mu}\) about \(\vec{k}\) at \(\omega_{\circ}\). Substitution gives an expression for this procession frequency

\[\begin{aligned}
\frac{d \mu_{x}}{d t} &=\frac{d}{d t} \mu_{\perp} \cos \omega_{0} t=-\mu_{\perp} \omega_{0} \sin \omega_{0} t \\[4pt]
&=\gamma H_{0} \mu_{y}=-\gamma H_{0} \sin \omega_{0} t
\end{aligned} \]

The effect is illustrated below:

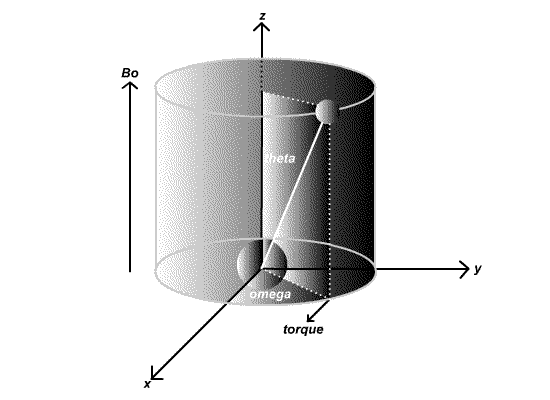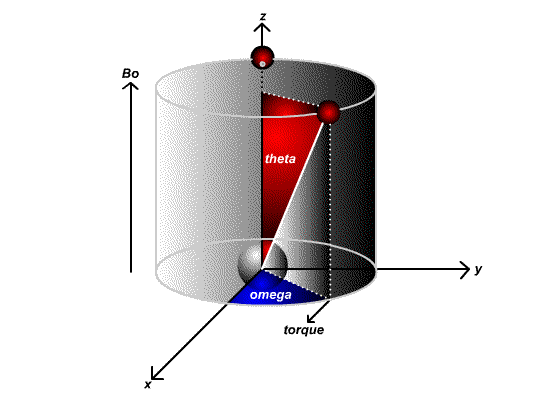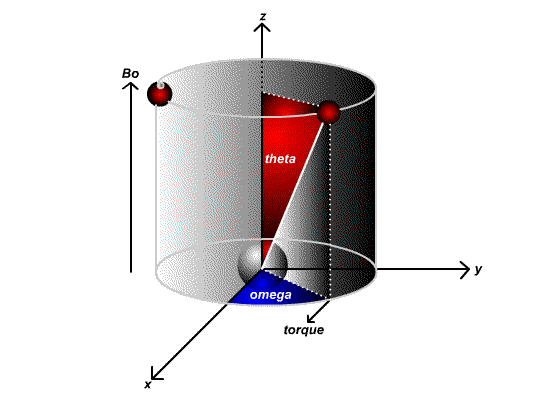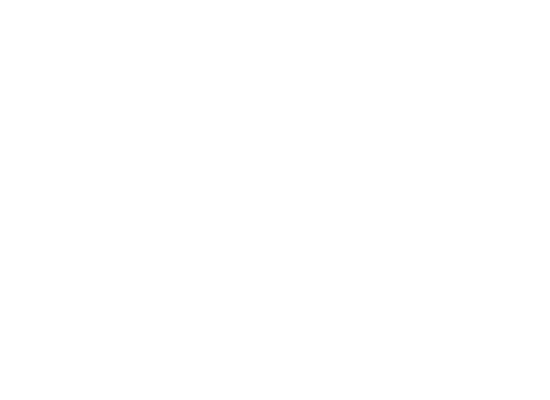
So \(\omega_{\circ}=\gamma H_{\circ}\) and this is the Larmour frequency, which is the procession of the nuclei due to the applied magnetic field which torques via magnetic moment due to the non-zero angular momentum (constantly spinning) of the nuclei.

So \(\omega_{\circ} \propto \gamma\) and \(\omega_{\circ} \propto H_{\circ}\).

Lamour frequency

• The larger the gyroscopic ratio for a nuclei, the greater the Lamour frequency
• The greater the applied magnetic field, the greater the Lamour Frequency.

Units

In NMR, is usually expressed in units of the nuclear magneton, \(\beta_{N}\):

\[\vec{\mu}_{N}=g_{N} \beta_{N} \nonumber \]

Where \(g_N\) is the nuclear g-value (unique to each nucleus). \(\beta_{N}\) is defined as

\[\beta_{N} \equiv \frac{e \hbar}{2 m_{p} c}=5.05 \times 10^{-27} \mathrm{JT}^{-1} \nonumber \]

Where c= charge of proton and is the mass of the proton. We have expressed the Larmour frequency in terms of \(\gamma\), the magnetogyric ratio. Recall:

\[\gamma=\frac{\vec{\mu}_{N}}{\vec{J}_{N}}=\frac{g_{N} \beta_{N}}{\hbar I}=\frac{2 \pi g_{N} \beta_{N}}{h I} \nonumber \]

Since \(\omega_{0}=\gamma H_{0}\) or \(2 \pi v_{0}=\gamma H_{0}\)

\[2 \pi v_{0}=\left(\frac{2 \pi g_{N} \beta_{N}}{h I}\right) H_{0} \nonumber \]

with

\[v_{0}=\frac{g_{N} \beta_{N} H_{0}}{h I} \nonumber \]

Example \(\PageIndex{1}\)

For H, with I=1/2, and g_N = 2.793. Calculate the Larmour frequency (in Hertz) for a field of 7.0463 Telsa (=70,463 Gauss).

Solution

\[\begin{aligned}
v_{\circ} &=\frac{g_{N} \beta_{N} H_{\circ}}{h I} \\[4pt] &=\frac{(2)(2.793)\left(5.05 \times 10^{-27}\right)(7.0463)}{6.626 \times 10^{-34}} H z \\[4pt] &=3 \times 10^{8} \mathrm{~Hz}
\end{aligned} \nonumber \]

Thus, NMR is commonly carried out at 300 MHz, which requires a 7 T magnetic field. The latter is produced in a superconducting solenoid (see Augustine or Britt labs for these).

Right: Magnet core of the largest superconducting solenoid magnet at European Organization for Nuclear Research's Large Hadron Collider.

References

1. Duer, M.J., Solid State NMR Spectroscopy: Principles and Applications. Blackwell Science Ltd. USA. 2002
2. Fukushima, E., Roeder, S.B.W., Experimental Pulse NMR A Nuts and Bolts Approach. Perseus Books Publishing, USA. 1981