2.15: Breaking Symmetries
- Page ID
- 366323
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Local Symmetry
Small modification of the molecule that reduces symmetry will have small effects on the spectra (e.g. \(\ce{H2CO}\) to \(\ce{CH3CHO}\)).
This gives same spectra patterns even though the point group of acetaldehyde is Cs, containing only two representations \(A’\) and \(A’’\) with \(x\), \(y\) = \(A’\) and \(z = A’’\). Thus, all transitions are symmetry allowed. Because of this, the idea of local symmetry is important. Local symmetry is that associated with the electronically active component of the molecule only, which is the \(\ce{C=O}\) moiety.
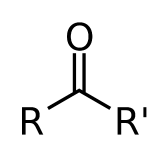
Independent of what \(R\) and \(R'\) are, provided that they not interact strongly with the C=O bond through conjugation etc. Hence this introduces the concept of a ”correlation or coherence length” of the excitation. Hence the UV-Vis spectra of all compounds of this type are similar: acetone, acetaldehyde, cyclopentanone, etc).
Acetone:
- \(π \rightarrow π{*}\) with \(λ_{max} = 188\, nm\) and \(ε= 1860\)
- \(n \rightarrow π^{*}\) with \(λ_{max} = 279 \,nm\) and \(ε= 15\)
vs. formaldehyde
- \(π \rightarrow π{*}\) with \(λ_{max} = 185\, nm\) and \(ε>10,000\)
- \(n \rightarrow π^{*}\) with \(λ_{max} = 270 nm\) and \(ε=100\)
Vibronic Coupling
The \({ }^{1} A_{2} \leftarrow{ }^{1} A_{1}\) transition is forbidden by symmetry selection rules for formaldehyde. Why do we see it in the \(\ce{H2CO}\) molecule at all? Answer= Vibronic coupling. The Born-Oppenheimer approximation is not absolute. There is always some interaction between vibrational and electronic motion in a molecule. This means that the separation
\[|q, r\rangle \approx |r; q\rangle_{e l}|q\rangle_{v i b} \nonumber \]
is not always exact. Thus we must consider the transition moment integral in its entirety.
\[\langle q, r|\hat{M}| q, r\rangle^{ex} \nonumber \]
Let’s assume \(|q, r\rangle\) is in its ground state for all vibrations (\(k_bT\) < all vibrational frequencies). The irreducible representation of all vibrations in non-excited state is \(A_1\). Thus \(|q, r\rangle\) has the symmetry of the electron wavefunction itself \(|r\rangle\). In general, the symmetry is the direct product of the symmetry representations of \(|r\rangle\) and \(|q\rangle\).
Now, for the excited state wavefunction (\(|q, r\rangle^{e x}\)), the symmetry is that of the electronic wavefunction (\(|r\rangle^{e x}\)) only if the vibrational state is totally symmetric (i.e. \(v’=0\)) for all normal modes or only \(A_1\) vibrations are excited. However, if one-quantum of a non-symmetric vibrational state is excited along with the electronic state (upon absorption of light), then the excited state representation will be:
\[\Gamma_{total} = \underbrace{\Gamma\left(|r\rangle^{r x}\right)}_{\text{vibration symmetry}} \otimes \underbrace{\Gamma\left(|q\rangle^{\jmath^{e x}}\right)}_{\text{electronic symmetry}} \nonumber \]
If \(\Gamma_{total}\) contains the same representation as a component of \(\hat{M}\) then the transition becomes weakly allowed vibrationally. Important, the appropriate vibrational mode is exited simultaneously with electronic transition.
\(\hat{M}\) in the \(C_{2v}\) point group has the following representations for \(x\), \(y\), and \(z\) polarizations:
\[\left(\begin{array}{c}
M_{x} \\
M_{y} \\
M_{z}
\end{array}\right) = \left(\begin{array}{c}
B_{1} \\
B_{2} \\
A_{1}
\end{array}\right).\nonumber \]
Hence, the \({ }^{1} A_{2}\left(n, \pi^{*}\right) \leftarrow{ }^{1} A_{1}\) transition in \(\ce{H2CO}\) transition can be vibronically coupled (allowed) if the quantum of a normal mode with symmetry:
- \(a_1\) giving a z-polarization
- \(b_1\) giving a y-polarization
- \(b_2\), giving a x-polarization
is simultaneously excited by the absorption of the photon. We can use this to predict the symmetries of the normal modes of vibration that a molecule has. A mode active in inducing an electronic transition (vibronically) is called an inducing mode or promoting mode.
Symmetry
Assume the electronic (lowest vibrational level) ground state is totally symmetry (e.g., closed shell) is usually the case for organic molecules. A transition may be vibronically induced by exciting one quantum of a vibrational mode of symmetry, , provided the direct produce
\[\Gamma_{q} \otimes \Gamma_{\hat{M}} \otimes \Gamma_{e x}=A_{1} \text { or } A_{1 g} \nonumber \]
where \(\Gamma_{\hat{M}}\) is the symmetry of the \(\hat{M}\) operator and \(\Gamma_{e x}\) is the symmetry of the electronic excited state. Of course, the allowed vibrations must contain one of the symmetry \(\Gamma_{v i b}\).
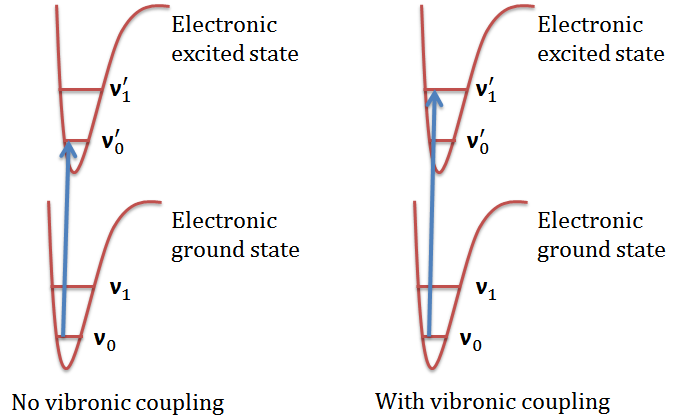
The \(\ce{0 -> 0}\) band does not appear in a vibrationally-induced electronic transition! This is one of its characteristics other than its reduced oscillator strength.
Possible vibrational modes for H2CO
A nonlinear molecule has \(3N-6\) internal degrees of vibrational freedom. These are these many vibrational frequencies, each of which has a symmetry of an irreducible representation for the molecular point group (https://www.chem.purdue.edu/jmol/vibs/form.html). For formaldehyde, with \(N=4\), we have \(3 \times 4-6=6\) vibrational degrees of freedom which are distributed as normal modes comprising of a superposition of local modes. These turn out to (we will discuss later) transform as: \({3a_1, b_1, 2b_2}\).
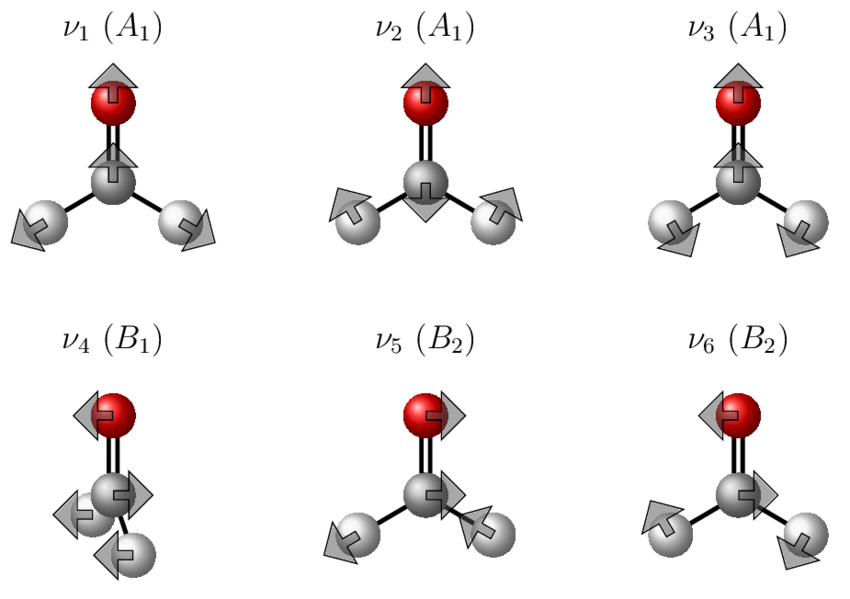
Thus only \(b_1\) and \(b_2\) unsymmetrical modes are possible? We can thus have no Z-polarized vibronic transitions (no \(a_2\) mode in H2CO), but we can have x- and y-polarized vibronic transition with \(b_2\) and \(b_1\) inducing modes, respectively. Hence, we can use polarization to identify inducing modes for vibronic transitions.
The \(\ce{d -> d}\) transitions in octahedral complexes are electronically forbidden (Laporte forbidden since they are \(\ce{g <-> g}\)), but they can be weakly allowed vibrationally by vibrations that remove the inversion center. Let’s consider the \(\ce{(NH3)6Co^{III}}\) complex that has a \(d^6\) configuration (loss of two 4s electrons and one d electron to make the ion).

The ground state is \(t_{2g}\) and the excited state \(e_{g}\). Is a d-d transition allowed?
The ground state symmetry is and has a \(O_h\) symmetry of ground state configuration due to the octahedral ligand field. Let’s consider the potential electronic \(\ce{d -> d}\) transition from the \(t_{2g}\) orbitals to the \(e_{g}\) orbitals. The excited electronic state symmetries are obtained from the orbital direct product:
\[\Gamma_{t_{2 g}} \otimes \Gamma_{e_{g}}=T_{1 g}+T_{2 g} \nonumber \]
(From direct product table for Oh)
Both \({ }^{1} T_{2 g} \leftarrow{ }^{1} A_{1 g}\) and \({ }^{1} T_{1 g} \leftarrow{ }^{1} A_{1 g}\) transitions are forbidden. Now, \(\hat{M}\) or \(\{x,\,y,\,z\}\) form the basis for a triply degenerate representation \(T_{1u}\) in \(O_h\).
| Oh | E | 8C3 | 6C2 | 6C4 | 3C2 =(C4)2 | i | 6S4 | 8S6 | 3σh | 6σd |
linear functions, rotations |
quadratic functions |
cubic functions |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1g | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | - | x2+y2+z2 | - |
| A2g | +1 | +1 | -1 | -1 | +1 | +1 | -1 | +1 | +1 | -1 | - | - | - |
| Eg | +2 | -1 | 0 | 0 | +2 | +2 | 0 | -1 | +2 | 0 | - | (2z2-x2-y2, x2-y2) | - |
| T1g | +3 | 0 | -1 | +1 | -1 | +3 | +1 | 0 | -1 | -1 | (Rx, Ry, Rz) | - | - |
| T2g | +3 | 0 | +1 | -1 | -1 | +3 | -1 | 0 | -1 | +1 | - | (xz, yz, xy) | - |
| A1u | +1 | +1 | +1 | +1 | +1 | -1 | -1 | -1 | -1 | -1 | - | - | - |
| A2u | +1 | +1 | -1 | -1 | +1 | -1 | +1 | -1 | -1 | +1 | - | - | xyz |
| Eu | +2 | -1 | 0 | 0 | +2 | -2 | 0 | +1 | -2 | 0 | - | - | - |
| T1u | +3 | 0 | -1 | +1 | -1 | -3 | -1 | 0 | +1 | +1 | (x, y, z) | - | (x3, y3, z3) [x(z2+y2), y(z2+x2), z(x2+y2)] |
| T2u | +3 | 0 | +1 | -1 | -1 | -3 | +1 | 0 | +1 | -1 | - | - | [x(z2-y2), y(z2-x2), z(x2-y2)] |
For instance, for the purely electronic transition \({ }^{1}T_{1 g} \leftarrow { }^{1} A_{1 g}\) component,
\[T_{1 g} \otimes T_{1 u} \otimes A_{1 g}=A_{1 u}+E_{u}+T_{1 g}+T_{2 u} \nonumber \]
this does not contain the \(A_{1g}\) symmetry representation (i.e., Laporte forbidden) and is therefore, this is a forbidden electronic transition.
What vibrations will couple these two electronic states? An octahedral complex (7 atoms so there are \(3 \times 7-6=15\) normal modes) has the following vibrational symmetries (discussed later):
\[\Gamma_{vib}=a_{1 g}+e_{g}+2 t_{1 u}+t_{2 g}+t_{2 u} \nonumber \]
(15 modes here, count them up)
The potential promoting modes are the \( 2t_{1u}\) and \(t_{2u}\) normal modes. The \(t_{1u}\) mode will serve as a promoting mode provided
\[\begin{aligned}
&T_{1 u} \otimes\left\{T_{1 g} \otimes T_{1 u} \otimes A_{1 g}\right\}= \\
&T_{1 u} \otimes\left[A_{1 u}+E_{u}+T_{1 u}+T_{2 u}\right]=A_{1 g}
\end{aligned} \nonumber \]
This turns out to contain \(A_{1g}\), so the \(t_{1u}\)’s can serve as a promoting mode for a vibrationally allowed transition. So it turns out, also can the \(t_{2u}\) mode.

