7.2.4: Crystal Defects
- Last updated
- Save as PDF
- Page ID
- 263189
 |
Prince George's Community College |
 |
| Unit I: Atoms Unit II: Molecules Unit III: States of Matter Unit IV: Reactions Unit V: Kinetics & Equilibrium Unit VI: Thermo & Electrochemistry Unit VII: Nuclear Chemistry |
||
Learning Objective
- To understand the origin and nature of defects in crystals.
The crystal lattices we have described represent an idealized, simplified system that can be used to understand many of the important principles governing the behavior of solids. In contrast, real crystals contain large numbers of defectsErrors in an idealized crystal lattice. (typically more than 104 per milligram), ranging from variable amounts of impurities to missing or misplaced atoms or ions. These defects occur for three main reasons:
- It is impossible to obtain any substance in 100% pure form. Some impurities are always present.
- Even if a substance were 100% pure, forming a perfect crystal would require cooling the liquid phase infinitely slowly to allow all atoms, ions, or molecules to find their proper positions. Cooling at more realistic rates usually results in one or more components being trapped in the “wrong” place in a lattice or in areas where two lattices that grew separately intersect.
- Applying an external stress to a crystal, such as a hammer blow, can cause microscopic regions of the lattice to move with respect to the rest, thus resulting in imperfect alignment.
In this section, we discuss how defects determine some of the properties of solids. We begin with solids that consist of neutral atoms, specifically metals, and then turn to ionic compounds.
Defects in Metals
Metals can have various types of defects. A point defectA defect in a crystal that affects a single point in the lattice. is any defect that involves only a single particle (a lattice point) or sometimes a very small set of points. A line defectA defect in a crystal that affects a row of points in the lattice. is restricted to a row of lattice points, and a plane defectA defect in a crystal that affects a plane of points in the lattice. involves an entire plane of lattice points in a crystal. A vacancyA point defect that consists of a single atom missing from a site in a crystal. occurs where an atom is missing from the normal crystalline array; it constitutes a tiny void in the middle of a solid (Figure 8.4.1). We focus primarily on point and plane defects in our discussion because they are encountered most frequently.
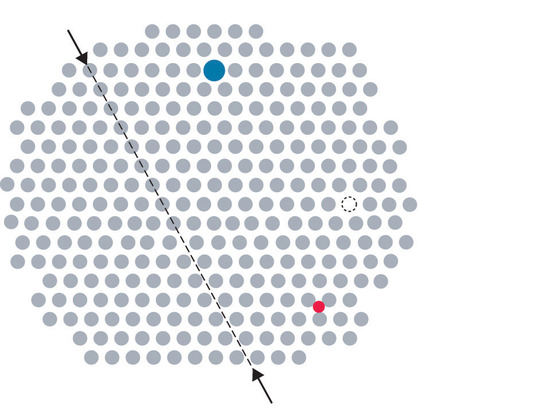
Figure 8.4.1Common Defects in Crystals In this two-dimensional representation of a crystal lattice containing substitutional and interstitial impurities, vacancies, and line defects, a dashed line and arrows indicate the position of the line defect.
Impurities
Impurities can be classified as interstitial or substitutional. An interstitial impurityA point defect that results when an impurity atom occupies an octahedral hole or a tetrahedral hole in the lattice between atoms. is usually a smaller atom (typically about 45% smaller than the host) that can fit into the octahedral or tetrahedral holes in the metal lattice (Figure 8.4.1). Steels consist of iron with carbon atoms added as interstitial impurities (Table 8.4.1 ). The inclusion of one or more transition metals or semimetals can improve the corrosion resistance of steel.
Table 8.4.1Compositions, Properties, and Uses of Some Types of Steel
| Name of Steel | Typical Composition* | Properties | Applications |
|---|---|---|---|
| low-carbon | <0.15% C | soft and ductile | wire |
| mild carbon | 0.15%–0.25% C | malleable and ductile | cables, chains, and nails |
| high-carbon | 0.60%–1.5% C | hard and brittle | knives, cutting tools, drill bits, and springs |
| stainless | 15%–20% Cr, 1%–5% Mn, 5%–10% Ni, 1%–3% Si, 1% C, 0.05% P | corrosion resistant | cutlery, instruments, and marine fittings |
| invar | 36% Ni | low coefficient of thermal expansion | measuring tapes and meter sticks |
| manganese | 10%–20% Mn | hard and wear resistant | armor plate, safes, and rails |
| high-speed | 14%–20% W | retains hardness at high temperatures | high-speed cutting tools |
| silicon | 1%–5% Si | hard, strong, and highly magnetic | magnets in electric motors and transformers |
| *In addition to enough iron to bring the total percentage up to 100%, most steels contain small amounts of carbon (0.5%–1.5%) and manganese (<2%). | |||
In contrast, a substitutional impurityA point defect that results when an impurity atom occupies a normal lattice site. is a different atom of about the same size that simply replaces one of the atoms that compose the host lattice (Figure 8.4.1 \). Substitutional impurities are usually chemically similar to the substance that constitutes the bulk of the sample, and they generally have atomic radii that are within about 15% of the radius of the host. For example, strontium and calcium are chemically similar and have similar radii, and as a result, strontium is a common impurity in crystalline calcium, with the Sr atoms randomly occupying sites normally occupied by Ca.
Note the Pattern
Interstitial impurities are smaller atoms than the host atom, whereas substitutional impurities are usually chemically similar and are similar in size to the host atom.
Dislocations, Deformations, and Work Hardening
Inserting an extra plane of atoms into a crystal lattice produces an edge dislocationA crystal defect that results from the insertion of an extra plane of atoms into part of the crystal lattice.. A familiar example of an edge dislocation occurs when an ear of corn contains an extra row of kernels between the other rows (Figure 8.4.2). An edge dislocation in a crystal causes the planes of atoms in the lattice to deform where the extra plane of atoms begins (Figure 8.4.2). The edge dislocation frequently determines whether the entire solid will deform and fail under stress.
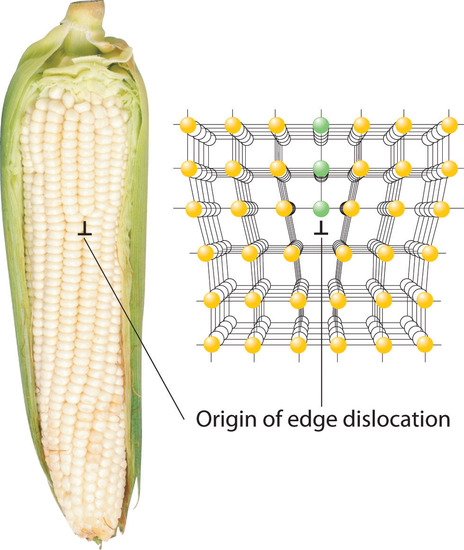
Figure 8.4.2 Edge Dislocations Shown are two examples of edge dislocations: (a) an edge dislocation in an ear of corn and (b) a three-dimensional representation of an edge dislocation in a solid, illustrating how an edge dislocation can be viewed as a simple line defect arising from the insertion of an extra set of atoms into the lattice. In both cases, the origin of the edge dislocation is indicated by the symbol ⊥
DeformationA distortion that occurs when a dislocation moves through a crystal. occurs when a dislocation moves through a crystal. To illustrate the process, suppose you have a heavy rug that is lying a few inches off-center on a nonskid pad. To move the rug to its proper place, you could pick up one end and pull it. Because of the large area of contact between the rug and the pad, however, they will probably move as a unit. Alternatively, you could pick up the rug and try to set it back down exactly where you want it, but that requires a great deal of effort (and probably at least one extra person). An easier solution is to create a small wrinkle at one end of the rug (an edge dislocation) and gradually push the wrinkle across, resulting in a net movement of the rug as a whole (part (a) in Figure 8.4.3). Moving the wrinkle requires only a small amount of energy because only a small part of the rug is actually moving at any one time. Similarly, in a solid, the contacts between layers are broken in only one place at a time, which facilitates the deformation process.
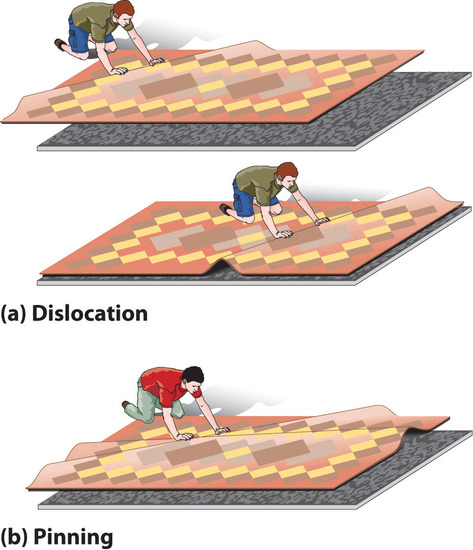
Figure 8.4.3 The Role of Dislocation in the Motion of One Planar Object across Another (a) Pushing a wrinkle across the rug results in a net movement of the rug with relatively little expenditure of energy because at any given time only a very small amount of the rug is not in contact with the floor. (b) A second intersecting wrinkle prevents movement of the first by “pinning” it.
If the rug we have just described has a second wrinkle at a different angle, however, it is very difficult to move the first one where the two wrinkles intersect (part (b) in Figure 8.4.3); this process is called pinningA process that increases the mechanical strength of a material by introducing multiple defects into a material so that the presence of one defect prevents the motion of another.. Similarly, intersecting dislocations in a solid prevent them from moving, thereby increasing the mechanical strength of the material. In fact, one of the major goals of materials science is to find ways to pin dislocations to strengthen or harden a material.
Pinning can also be achieved by introducing selected impurities in appropriate amounts. Substitutional impurities that are a mismatch in size to the host prevent dislocations from migrating smoothly along a plane. Generally, the higher the concentration of impurities, the more effectively they block migration, and the stronger the material. For example, bronze, which contains about 20% tin and 80% copper by mass, produces a much harder and sharper weapon than does either pure tin or pure copper. Similarly, pure gold is too soft to make durable jewelry, so most gold jewelry contains 75% (18 carat) or 58% (14 carat) gold by mass, with the remainder consisting of copper, silver, or both.
If an interstitial impurity forms polar covalent bonds to the host atoms, the layers are prevented from sliding past one another, even when only a small amount of the impurity is present. For example, because iron forms polar covalent bonds to carbon, the strongest steels need to contain only about 1% carbon by mass to substantially increase their strength (Table 8.4.1).
Most materials are polycrystalline, which means they consist of many microscopic individual crystals called grains that are randomly oriented with respect to one another. The place where two grains intersect is called a grain boundaryThe place where two grains in a solid intersect.. The movement of a deformation through a solid tends to stop at a grain boundary. Consequently, controlling the grain size in solids is critical for obtaining desirable mechanical properties; fine-grained materials are usually much stronger than coarse-grained ones.
Grain boundaries. As a polycrystalline material solidifies, grains with irregular shapes form. The interfaces between grains constitute grain boundaries. (Squares represent unit cells within grains.)
Work hardeningThe practice of introducing a dense network of dislocations throughout a solid, making it very tough and hard. is the introduction of a dense network of dislocations throughout a solid, which makes it very tough and hard. If all the defects in a single 1 cm3 sample of a work-hardened material were laid end to end, their total length could be 106 km! The legendary blades of the Japanese and Moorish swordsmiths owed much of their strength to repeated work hardening of the steel. As the density of defects increases, however, the metal becomes more brittle (less malleable). For example, bending a paper clip back and forth several times increases its brittleness from work hardening and causes the wire to break.
Memory Metal
The compound NiTi, popularly known as “memory metal” or nitinol (nickel–titanium Naval Ordinance Laboratory, after the site where it was first prepared), illustrates the importance of deformations. If a straight piece of NiTi wire is wound into a spiral, it will remain in the spiral shape indefinitely, unless it is warmed to 50°C–60°C, at which point it will spontaneously straighten out again. The chemistry behind the temperature-induced change in shape is moderately complex, but for our purposes it is sufficient to know that NiTi can exist in two different solid phases.
The high-temperature phase has the cubic cesium chloride structure, in which a Ti atom is embedded in the center of a cube of Ni atoms (or vice versa). The low-temperature phase has a related but kinked structure, in which one of the angles of the unit cell is no longer 90°. Bending an object made of the low-temperature (kinked) phase creates defects that change the pattern of kinks within the structure. If the object is heated to a temperature greater than about 50°C, the material undergoes a transition to the cubic high-temperature phase, causing the object to return to its original shape. The shape of the object above 50°C is controlled by a complex set of defects and dislocations that can be relaxed or changed only by the thermal motion of the atoms.
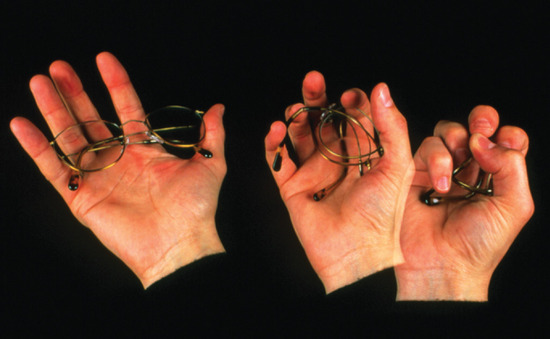
Memory metal. Flexon is a fatigue-resistant alloy of Ti and Ni that is used as a frame for glasses because of its durability and corrosion resistance.
Memory metal has many other practical applications, such as its use in temperature-sensitive springs that open and close valves in the automatic transmissions of cars. Because NiTi can also undergo pressure- or tension-induced phase transitions, it is used to make wires for straightening teeth in orthodontic braces and in surgical staples that change shape at body temperature to hold broken bones together
Another flexible, fatigue-resistant alloy composed of titanium and nickel is Flexon. Originally discovered by metallurgists who were creating titanium-based alloys for use in missile heat shields, Flexon is now used as a durable, corrosion-resistant frame for glasses, among other uses.
Example 8.4.1
Because steels with at least 4% chromium are much more corrosion resistant than iron, they are collectively sold as “stainless steel.” Referring to the composition of stainless steel in Table 8.4.1 and, if needed, the atomic radii in Figure 3.1.7, predict which type of impurity is represented by each element in stainless steel, excluding iron, that are present in at least 0.05% by mass.
Given: composition of stainless steel and atomic radii
Asked for: type of impurity
Strategy:
Using the data in Table 8.4.1 and the atomic radii in Figure 3.1.7, determine whether the impurities listed are similar in size to an iron atom. Then determine whether each impurity is chemically similar to Fe. If similar in both size and chemistry, the impurity is likely to be a substitutional impurity. If not, it is likely to be an interstitial impurity.
Solution:
According to Table 8.4.1 stainless steel typically contains about 1% carbon, 1%–5% manganese, 0.05% phosphorus, 1%–3% silicon, 5%–10% nickel, and 15%–20% chromium. The three transition elements (Mn, Ni, and Cr) lie near Fe in the periodic table, so they should be similar to Fe in chemical properties and atomic size (atomic radius = 125 pm). Hence they almost certainly will substitute for iron in the Fe lattice. Carbon is a second-period element that is nonmetallic and much smaller (atomic radius = 77 pm) than iron. Carbon will therefore tend to occupy interstitial sites in the iron lattice. Phosphorus and silicon are chemically quite different from iron (phosphorus is a nonmetal, and silicon is a semimetal), even though they are similar in size (atomic radii of 106 and 111 pm, respectively). Thus they are unlikely to be substitutional impurities in the iron lattice or fit into interstitial sites, but they could aggregate into layers that would constitute plane defects.
Exercise
Consider nitrogen, vanadium, zirconium, and uranium impurities in a sample of titanium metal. Which is most likely to form an interstitial impurity? a substitutional impurity?
Answer: nitrogen; vanadium
Defects in Ionic and Molecular Crystals
All the defects and impurities described for metals are seen in ionic and molecular compounds as well. Because ionic compounds contain both cations and anions rather than only neutral atoms, however, they exhibit additional types of defects that are not possible in metals.
The most straightforward variant is a substitutional impurity in which a cation or an anion is replaced by another of similar charge and size. For example, Br− can substitute for Cl−, so tiny amounts of Br− are usually present in a chloride salt such as CaCl2 or BaCl2. If the substitutional impurity and the host have different charges, however, the situation becomes more complicated. Suppose, for example, that Sr2+ (ionic radius = 118 pm) substitutes for K+ (ionic radius = 138 pm) in KCl. Because the ions are approximately the same size, Sr2+ should fit nicely into the face-centered cubic (fcc) lattice of KCl. The difference in charge, however, must somehow be compensated for so that electrical neutrality is preserved. The simplest way is for a second K+ ion to be lost elsewhere in the crystal, producing a vacancy. Thus substitution of K+ by Sr2+ in KCl results in the introduction of two defects: a site in which an Sr2+ ion occupies a K+ position and a vacant cation site. Substitutional impurities whose charges do not match the host’s are often introduced intentionally to produce compounds with specific properties.
Virtually all the colored gems used in jewelry are due to substitutional impurities in simple oxide structures. For example, α-Al2O3, a hard white solid called corundum that is used as an abrasive in fine sandpaper, is the primary component, or matrix, of a wide variety of gems. Because many trivalent transition metal ions have ionic radii only a little larger than the radius of Al3+ (ionic radius = 53.5 pm), they can replace Al3+ in the octahedral holes of the oxide lattice. Substituting small amounts of Cr3+ ions (ionic radius = 75 pm) for Al3+ gives the deep red color of ruby, and a mixture of impurities (Fe2+, Fe3+, and Ti4+) gives the deep blue of sapphire. True amethyst contains small amounts of Fe3+ in an SiO2 (quartz) matrix. The same metal ion substituted into different mineral lattices can produce very different colors. For example, Fe3+ ions are responsible for the yellow color of topaz and the violet color of amethyst. The distinct environments cause differences in d orbital energies, enabling the Fe3+ ions to absorb light of different frequencies.

The same cation in different environments. An Fe3+ substitutional impurity produces substances with strikingly different colors.
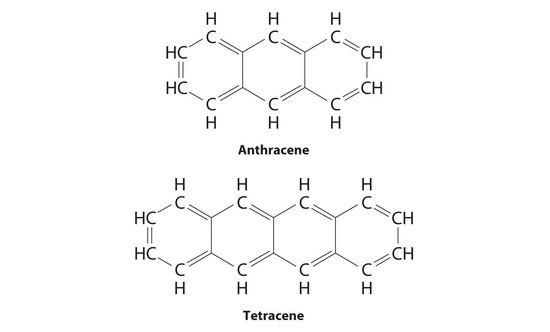
Substitutional impurities are also observed in molecular crystals if the structure of the impurity is similar to the host, and they can have major effects on the properties of the crystal. Pure anthracene, for example, is an electrical conductor, but the transfer of electrons through the molecule is much slower if the anthracene crystal contains even very small amounts of tetracene despite their strong structural similarities.
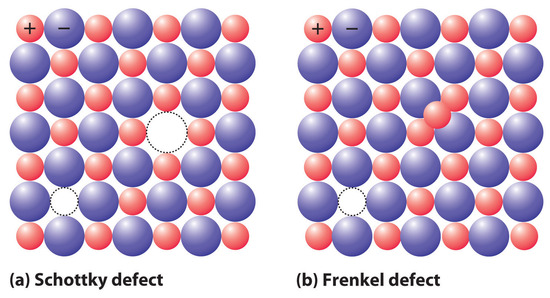
If a cation or an anion is simply missing, leaving a vacant site in an ionic crystal, then for the crystal to be electrically neutral, there must be a corresponding vacancy of the ion with the opposite charge somewhere in the crystal. In compounds such as KCl, the charges are equal but opposite, so one anion vacancy is sufficient to compensate for each cation vacancy. In compounds such as CaCl2, however, two Cl− anion sites must be vacant to compensate for each missing Ca2+ cation. These pairs (or sets) of vacancies are called Schottky defectsA coupled pair of vacancies—one cation and one anion—that maintains the electrical neutrality of an ionic solid. and are particularly common in simple alkali metal halides such as KCl (part (a) in Figure 8.4.4). Many microwave diodes, which are devices that allow a current to flow in a single direction, are composed of materials with Schottky defects.
Figure 8.4.4 The Two Most Common Defects in Ionic Solids (a) A Schottky defect in KCl shows the missing cation/anion pair. (b) A Frenkel defect in AgI shows a misplaced Ag+ cation.
Occasionally one of the ions in an ionic lattice is simply in the wrong position. An example of this phenomenon, called a Frenkel defectA defect in an ionic lattice that occurs when one of the ions is in the wrong position., is a cation that occupies a tetrahedral hole rather than an octahedral hole in the anion lattice (part (b) in Figure 8.4.4). Frenkel defects are most common in salts that have a large anion and a relatively small cation. To preserve electrical neutrality, one of the normal cation sites, usually octahedral, must be vacant.
Frenkel defects are particularly common in the silver halides AgCl, AgBr, and AgI, which combine a rather small cation (Ag+, ionic radius = 115 pm) with large, polarizable anions. Certain more complex salts with a second cation in addition to Ag+ and Br− or I− have so many Ag+ ions in tetrahedral holes that they are good electrical conductors in the solid state; hence they are called solid electrolytesA solid material with a very high electrical conductivity.. (As you will learn in Chapter 12, most ionic compounds do not conduct electricity in the solid state, although they do conduct electricity when molten or dissolved in a solvent that separates the ions, allowing them to migrate in response to an applied electric field.) In response to an applied voltage, the cations in solid electrolytes can diffuse rapidly through the lattice via octahedral holes, creating Frenkel defects as the cations migrate. Sodium–sulfur batteries use a solid Al2O3 electrolyte with small amounts of solid Na2O. Because the electrolyte cannot leak, it cannot cause corrosion, which gives a battery that uses a solid electrolyte a significant advantage over one with a liquid electrolyte.
Example 8.4.2
In a sample of NaCl, one of every 10,000 sites normally occupied by Na+ is occupied instead by Ca2+. Assuming that all of the Cl− sites are fully occupied, what is the stoichiometry of the sample?
Given: ionic solid and number and type of defect
Asked for: stoichiometry
Strategy:
A Identify the unit cell of the host compound. Compute the stoichiometry if 0.01% of the Na+ sites are occupied by Ca2+. If the overall charge is greater than 0, then the stoichiometry must be incorrect.
B If incorrect, adjust the stoichiometry of the Na+ ion to compensate for the additional charge.
Solution:
A Pure NaCl has a 1:1 ratio of Na+ and Cl− ions arranged in an fcc lattice (the sodium chloride structure). If all the anion sites are occupied by Cl−, the negative charge is −1.00 per formula unit. If 0.01% of the Na+ sites are occupied by Ca2+ ions, the cation stoichiometry is Na0.99Ca0.01. This results in a positive charge of (0.99)(+1) + (0.01)(+2) = +1.01 per formula unit, for a net charge in the crystal of +1.01 + (−1.00) = +0.01 per formula unit. Because the overall charge is greater than 0, this stoichiometry must be incorrect.
B The most plausible way for the solid to adjust its composition to become electrically neutral is for some of the Na+ sites to be vacant. If one Na+ site is vacant for each site that has a Ca2+ cation, then the cation stoichiometry is Na0.98Ca0.01. This results in a positive charge of (0.98)(+1) + (0.01)(+2) = +1.00 per formula unit, which exactly neutralizes the negative charge. The stoichiometry of the solid is thus Na0.98Ca0.01Cl1.00.
Exercise
In a sample of MgO that has the sodium chloride structure, 0.02% of the Mg2+ ions are replaced by Na+ ions. Assuming that all of the cation sites are fully occupied, what is the stoichiometry of the sample?
Answer: If the formula of the compound is Mg0.98Na0.02O1−x, then x must equal 0.01 to preserve electrical neutrality. The formula is thus Mg0.98Na0.02O0.99.
Nonstoichiometric Compounds
The law of multiple proportions, states that chemical compounds contain fixed integral ratios of atoms. In fact, nonstoichiometric compoundsA solid that has intrinsically variable stoichiometries without affecting the fundamental structure of the crystal. contain large numbers of defects, usually vacancies, which give rise to stoichiometries that can depart significantly from simple integral ratios without affecting the fundamental structure of the crystal. Nonstoichiometric compounds frequently consist of transition metals, lanthanides, and actinides, with polarizable anions such as oxide (O2−) and sulfide (S2−). Some common examples are listed in Table 8.4.1, along with their basic structure type. These compounds are nonstoichiometric because their constituent metals can exist in multiple oxidation states in the solid, which in combination preserve electrical neutrality.
Table 12.4.1 Some Non-stoichiometric Compounds
| Compound | Observed Range of x |
|---|---|
| Oxides* | |
| FexO | 0.85–0.95 |
| NixO | 0.97–1.00 |
| TiOx | 0.75–1.45 |
| VOx | 0.9–1.20 |
| NbOx | 0.9–1.04 |
| Sulfides | |
| CuxS | 1.77–2.0 |
| FexS | 0.80–0.99 |
| ZrSx | 0.9–1.0 |
| *All the oxides listed have the sodium chloride structure. | |
One example is iron(II) oxide (ferrous oxide), which produces the black color in clays and is used as an abrasive. Its stoichiometry is not FeO because it always contains less than 1.00 Fe per O2− (typically 0.90–0.95). This is possible because Fe can exist in both the +2 and +3 oxidation states. Thus the difference in charge created by a vacant Fe2+ site can be balanced by two Fe2+ sites that have Fe3+ ions instead [+2 vacancy = (3 − 2) + (3 − 2)]. The crystal lattice is able to accommodate this relatively high fraction of substitutions and vacancies with no significant change in structure.
Note the Pattern
Because a crystal must be electrically neutral, any defect that affects the number or charge of the cations must be compensated by a corresponding defect in the number or charge of the anions.
Summary
Real crystals contain large numbers of defects. Defects may affect only a single point in the lattice (a point defect), a row of lattice points (a line defect), or a plane of atoms (a plane defect). A point defect can be an atom missing from a site in the crystal (a vacancy) or an impurity atom that occupies either a normal lattice site (a substitutional impurity) or a hole in the lattice between atoms (an interstitial impurity). In an edge dislocation, an extra plane of atoms is inserted into part of the crystal lattice. Multiple defects can be introduced into materials so that the presence of one defect prevents the motion of another, in a process called pinning. Because defect motion tends to stop at grain boundaries, controlling the size of the grains in a material controls its mechanical properties. In addition, a process called work hardening introduces defects to toughen metals. Schottky defects are a coupled pair of vacancies—one cation and one anion—that maintains electrical neutrality. A Frenkel defect is an ion that occupies an incorrect site in the lattice. Cations in such compounds are often able to move rapidly from one site in the crystal to another, resulting in high electrical conductivity in the solid material. Such compounds are called solid electrolytes. Nonstoichiometric compounds have variable stoichiometries over a given range with no dramatic change in crystal structure. This behavior is due to a large number of vacancies or substitutions of one ion by another ion with a different charge.
Key Takeaway
- Defects determine the behavior of solids, but because ionic compounds contain both cations and anions, they exhibit additional types of defects that are not found in metals.
Conceptual Problems
-
How are defects and impurities in a solid related? Can a pure, crystalline compound be free of defects? How can a substitutional impurity produce a vacancy?
-
Why does applying a mechanical stress to a covalent solid cause it to fracture? Use an atomic level description to explain why a metal is ductile under conditions that cause a covalent solid to fracture.
-
How does work hardening increase the strength of a metal? How does work hardening affect the physical properties of a metal?
-
Work-hardened metals and covalent solids such as diamonds are both susceptible to cracking when stressed. Explain how such different materials can both exhibit this property.
-
Suppose you want to produce a ductile material with improved properties. Would impurity atoms of similar or dissimilar atomic size be better at maintaining the ductility of a metal? Why? How would introducing an impurity that forms polar covalent bonds with the metal atoms affect the ductility of the metal? Explain your reasoning.
-
Substitutional impurities are often used to tune the properties of material. Why are substitutional impurities generally more effective at high concentrations, whereas interstitial impurities are usually effective at low concentrations?
-
If an O2− ion (ionic radius = 132 pm) is substituted for an F− ion (ionic radius = 133 pm) in an ionic crystal, what structural changes in the ionic lattice will result?
-
How will the introduction of a metal ion with a different charge as an impurity induce the formation of oxygen vacancies in an ionic metal-oxide crystal?
-
Many nonstoichiometric compounds are transition metal compounds. How can such compounds exist, given that their nonintegral cation:anion ratios apparently contradict one of the basic tenets of Dalton’s atomic theory of matter?
-
If you wanted to induce the formation of oxygen vacancies in an ionic crystal, which would you introduce as substitutional impurities—cations with a higher positive charge or a lower positive charge than the cations in the parent structure? Explain your reasoning.
Answers
-
-
-
-
-
Impurity atoms of similar size and with similar chemical properties would be most likely to maintain the ductility of the metal, because they are unlikely to have a large effect on the ease with which one layer of atoms can move past another under mechanical stress. Larger impurity atoms are likely to form “bumps” or kinks that will make it harder for layers of atoms to move across one another. Interstitial atoms that form polar covalent bonds with the metal atoms tend to occupy spaces between the layers; they act as a “glue” that holds layers of metal atoms together, which greatly decreases the ductility.
-
-
Since O2− and F− are both very similar in size, substitution is possible without disruption of the ionic packing. The difference in charge, however, requires the formation of a vacancy on another F− site to maintain charge neutrality.
-
-
Most transition metals form at least two cations that differ by only one electron. Consequently, nonstoichiometric compounds containing transition metals can maintain electrical neutrality by gaining electrons to compensate for the absence of anions or the presence of additional metal ions. Conversely, such compounds can lose electrons to compensate for the presence of additional anions or the absence of metal ions. In both cases, the positive charge on the transition metal is adjusted to maintain electrical neutrality.
-
Numerical Problems
-
The ionic radius of K+ is 133 pm, whereas that of Na+ is 98 pm. Do you expect K+ to be a common substitutional impurity in compounds containing Na+? Why or why not?
-
Given Cs (262 pm), Tl (171 pm), and B (88 pm) with their noted atomic radii, which atom is most likely to act as an interstitial impurity in an Sn lattice (Sn atomic radius = 141 pm)? Why?
-
After aluminum, iron is the second most abundant metal in Earth’s crust. The silvery-white, ductile metal has a body-centered cubic (bcc) unit cell with an edge length of 286.65 pm.
- Use this information to calculate the density of iron.
- What would the density of iron be if 0.15% of the iron sites were vacant?
- How does the mass of 1.00 cm3 of iron without defects compare with the mass of 1.00 cm3 of iron with 0.15% vacancies?
-
Certain ceramic materials are good electrical conductors due to high mobility of oxide ions resulting from the presence of oxygen vacancies. Zirconia (ZrO2) can be doped with yttrium by adding Y2O3. If 0.35 g of Y2O3 can be incorporated into 25.0 g of ZrO2 while maintaining the zirconia structure, what is the percentage of oxygen vacancies in the structure?
-
Which of the following ions is most effective at inducing an O2− vacancy in crystal of CaO? The ionic radii are O2−, 132 pm; Ca2+, 100 pm; Sr2+, 127 pm; F−, 133 pm; La3+, 104 pm; and K+, 133 pm. Explain your reasoning.
Answers
-
No. The potassium is much larger than the sodium ion.
-
-
- 7.8744 g/cm3
- 7.86 g/cm3
- Without defects, the mass is 0.15% greater.
-
-
The lower charge of K+ makes it the best candidate for inducing an oxide vacancy, even though its ionic radius is substantially larger than that of Ca2+. Substituting two K+ ions for two Ca2+ ions will decrease the total positive charge by two, and an oxide vacancy will maintain electrical neutrality. For example, if 10% of the Ca2+ ions are replaced by K+, we can represent the change as going from Ca20O20 to K2Ca18O20, which has a net charge of +2. Loss of one oxide ion would give a composition of K2Ca18O19, which is electrically neutral.