7.E: Spectroscopy (Exercises)
- Page ID
- 50964
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)14.1: Vocabulary
Q14.2
Find the wave number and frequency of light with a wavelength of 700 nm (to three significant figures).
S14.2
1. Wave number is equal to the reciprocal of wavelength. Its units are inverse centimeters.
$$ \tilde \nu = \dfrac{1}{\lambda} \]
$$ \tilde \nu = \dfrac{1}{700\ nm} \times \dfrac{10^9\ nm}{100\ cm} \]
$$ \tilde \nu = 1.43\ \times 10^4\ cm^{-1} \]
2. Use the relationship between frequency, speed, and wavelength to solve for frequency.
$$ \nu = \dfrac{c}{\lambda} \]
$$ \nu = \dfrac{2.998\ \times 10^8\ m/s}{700\ nm \times \dfrac{m}{10^9\ nm}} \]
$$ \nu = 4.28 \times 10^{14}\ s^{-1} \]
Q14.2a
Convert \(3 \times 10^4\; cm^{-1}\) to wavelength. Identify what kind of spectroscopy?Q14.2a
What is the frequency and wavenumber of a 740 nm photon?Q14.2b
The wavelength of the red line in the Hydrogen spectrum is 656 nm (\(656 \times 10^{-9}\; m\)). What is the wavenumber and frequency of it?
S14.2b
The wave number =1/λ = 1/656 x10-9 m = 1.5x106 m-1
Q14.2c
Convert 533 nm to wavenumber and frequency.Q14.4a
Convert the following absorbance to percent transmittance: (a) 0.56, (b) 1.5, (c) 6.8.Q14.4b
Calculate percent transmittance from the following values of absorbance:
- 4.0
- 0.23
- 1.6
S14.4b
Solve, using the relationship between transmittance and absorbance.
$$ -\log){10}T = A \]
$$ T = 10^{-A} \]
For percent transmittance, multiply T by 100%
(a)
$$ T = 10^{-4.0} \times 100\% \]
$$ T = 0.010\% \]
(b)
$$ T = 10^{-0.23} \times 100\% \]
$$ T = 59\%\]
(c)
$$ T = 10^{-1.6} \times 100\% \]
$$ T = 2.5\% \]
Answers: 0.010%, 59%, 2.5%
Q14.4c
Convert the following from percent transmittance to absorbance.- 0.10%
- 23%
- 84%
Q14.4c
What is the percent transmitter of the following absorbance
- 0.4
- 1.2
S14.4c
We have A = 2- log %T
a. 0.4 = 2-log%T -->%T= 10(2-0.4)
%T= 39.8
b. 1.2 = 2-log%T ---> %T = 6.3%
Q14.6a
Q14.6b
Find the uncertainty of simultaneously measuring the frequency and wavelength of an emission, if the wavelength is 430 nm and the excited state lifetime is 0.50 nanoseconds.
S14.6b
1. Use Heisenberg's uncertainty principle and the relationship between energy and frequency to find the uncertainty of frequency.
$$ \Delta E \Delta t \geq \dfrac{h}{4 \pi} \]
$$ \Delta E = h \Delta \nu \]
$$ h \Delta \nu \Delta t \geq \dfrac{h}{4 \pi} \]
$$ \Delta \nu \geq \dfrac{1}{4 \pi \Delta t} \]
The maximum value for Δt is the lifetime of the excited state.
$$ \Delta \nu \geq \dfrac{1}{4 \pi 0.50 ns \times \dfrac{s}{10^9\ ns}} \]
$$ \Delta \nu \geq 1.6 \times 10^8\ s^{-1} \]
2. Use the uncertainty of frequency and the relationship between frequency and wavelength to find the uncertainty of the wavelength.
$$ \lambda = \dfrac{c}{\nu} \]
$$ | \Delta \lambda | = \dfrac{c}{\nu^2} | \Delta \nu | \]
$$ | \Delta \lambda | = \dfrac{\lambda ^2 | \Delta \nu | }{c} \]
$$ | \Delta \lambda | = \dfrac{(430\ nm)^2 \times 1.6 \times 10^8\ s^{-1}}{2.998 \times 10^8\ m/s} \times \dfrac{m}{10^9\ nm} \]
$$ | \Delta \lambda | = 2.3 \times 10^{-7}\ nm \]
Q14.6c
Calculate the wavelength emission of an electronically excited molecule with uncertainties in frequency (∆v) is 5.6x106 s-1and the wavelength ( ∆λ) 4x10-6 nm? c= 3x108ms-1=3x1017nms-1
S14.6c
We have:
\[ |∆λ|= \dfrac{λ|∆v|}{v} \]
Since
\[ \nu = \dfrac{c/}{\lambda}\]
then
\[|∆λ|= \dfrac{λ^2|∆v|}{c} \]
=> 4x10-6nm = (λ2 x 5.6x106 s-1)/ 3x1017nms-1
=> λ = 463 nm
Q14.8a
In the gas phase, using electronic spectroscopy, what is observed on the electronic spectra of diatomic molecules at high resolution in terms of structure and bands?Q14.8b
Explain why the decreasing of temperature will increase the resolution of visible and UV spectra?
S14.8b
Decreasing temperature will lower the kinetic energy of molecules. Thus the effect of Doppler and collisional broadening decrease, making the resolution enhances.
Q14.8c
Q14.10
In a 5.0 mM solution, a solute absorbs 90% of a visible light as the beam passes through a 80 mm cell. Calculate the molar absorptivity of this solute.
S14.10
We can calculate the transmittance:
\[T = 1.00 - 0.9 = 0.10\]
Also, the absorbance is
\[A = -\log T = -\log (0.10) = 1.0\]
Next step, use Beer-Lambert law to determine the molar absorptivity,
\[ \epsilon = \dfrac{A}{bc}\]
\[ \epsilon = \dfrac{1}{(8.0\,cm)(5.0 \, mM)} = 2.5 \times 10^{-2} L \, mol^{-1} \, cm^{-1}\]
Q14.10
Calculate the absorbance (\(A\)) with the molar absorptivity= 6.17, c= 0.52 M when a certain wavelength passes through 2.3-cm cell.
S14.10
\[ A = \epsilon b c = (6.17) (2.3) (0.52) = 7.38\]
Q14.12
Calculate \(E_{vib}\) for a harmonic oscillator if \(v=2\) and \(\nu = 3.24 \times 10^{13} \;Hz\)
S14.12
\[E_{vib}=(v+\frac{1}{2})h\nu =(2+\frac{1}{2}) 6.626 \times 10^{-34} \times 3.24 \times 10^{13}= 5.37*10^{-20}Hz\]
Q14.24
Given the following molecules: CO2, H2O. Show the fundamental vibration modes for each of the molecule and explain which one are IR active or both.S14.24
Q14.26
Given the following molecules: He2, F2, H2, O2 and Li2. Rank these molecules from lowest to highest fundamental frequency of vibration? Show works.S14.26
This can be determined by looking at the mass of the molecules. The one with the lowest mass will have the highest fundamental frequency of vibration and vice versa.14.5: Nuclear Magnetic Resonance
Q14.12
A chemist used the NMR machine to scan his sample and he obtained a signal-to-noise (S/N) ratio of 2.0. How long would it takes the chemist to generate a spectrum with a S/N ratio of 40? Assumed he spent 5 minutes per scan.S14.12
We are looking at theQ14.28
Explain why pentacene crystals are blue in color, but tetracene crystals are orange.

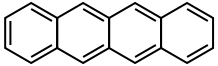
pentacene tetracene
Q14.29
Use the particle in a one-dimensional-box model to calculate the longest wavelength peak in the absorption spectrum of ß-carotene (structure shown below).
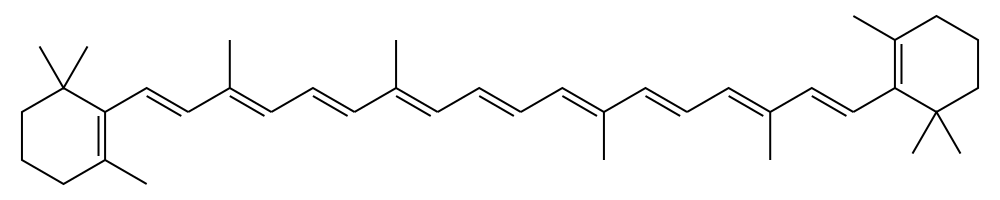
Q14.32a
What does chemical shift measure? What can influence chemical shift?S14.32a
Chemical shift measures the difference in resonance frequencies between a nucleus of interest and a reference nucleus. It is influenced by electron shielding; the more electrons are pulled away from a proton of interest (the smaller the electron density around the nucleus of interest), the greater the chemical shift.
Q14.32b
Q14.34b
Q14.32c
Identify the most shielded and deshielded hydrogen for this compound:

S14.32c
The hydrogen groups on the far right end are the most shielded and the hydrogen group on the carbon with the chlorine group is the most deshielded.
Q14.32d
The NMR signal of coumpound is 280 Hz downfield from TMS is 70 MHZ. find its chemical shifl in ppm.
S14.32d
\[δ = \dfrac{ \nu - \nu_{ref}}{ \nu_{spec}} \times 10^6\]
\[δ = \dfrac{ 280\; Hz }{ 70 \times 10^6} \times 10^6 = 4.0 \; ppm\]
Q14.34
- Calculate the magnetic field, B0 that corresponds to a precession frequency of 600 MHz for 1H.
- What is the field strength (in tesla) needed to generate a 1H frequency of 500 MHz?
- How do spin-spin relaxation and spin-lattice relaxation differ from each other?
- The 1H NMR spectrum of toluene shows that it has two peaks because of methyl and aromatic protons recorded at 60 MHz and 1.41 T. Given this information, what would be the magnetic field at 400 MHz?
- What is the difference between 13C and 1H NMR?
S14.34
- B0= 14.1 T.
- Using the equation used in problem 1 and solving it for B0we get a field strength of 11.74 T.
- Look under relaxation.
- Since we know that the NMR frequency is directly proportional to the magnetic strength, we calculate the magnetic field at 400 MHz: B0 = (400 MHz/60MHz) x 1.41 T = 9.40 T
- Look under applications.
Q14.34
calculate the field strength in tesla to generate 1H frequency of 300 MHz?
S14.34
B0 = 2πv/ɣ = 2π(300 x 106 s-1)/ 26.75 x 107 T-1s-1
B0 = 7.04 T
Q14.36
Given 4.7 T, calculate the diference in frequency for 2 protons whose § value differ 1.25 and 400 MHz
S14.36
B0 = (Δδ x vspec) / 106 = (1.25 (200 x 106 Hz)) / 106
B0 = 2.5 x 102 Hz
Q14.38
Draw the NMR spectrum of isobutyl alcohol with chemical shift -CH 0.90 ppm, -A-H 1.68ppm, -CH2 3.26 ppm, O-H 4.49 ppm
S14.38
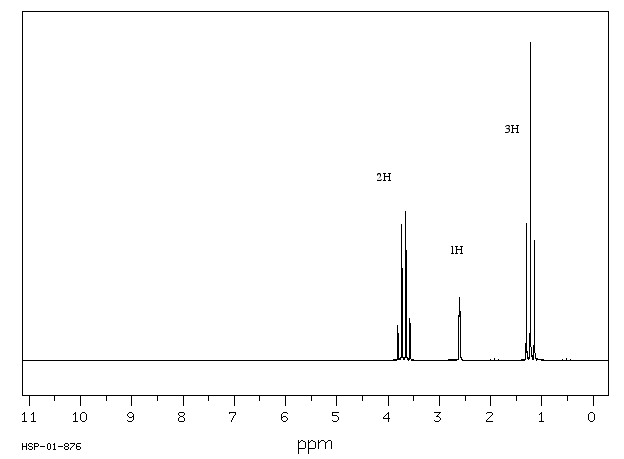
14.6: Electron Spin Resonance
Q14.42
14.7: Fluorescence and Phosphorescence
Q14.43
Someone has handed you data of the luminescence of a material as a function of time. How can you decide whether the luminescence process was fluorescence or phosphorescence?

