15.6: Disturbing a Chemical Equilibrium
- Page ID
- 60738
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
Hopefully you have come to realize that if you mix reactants a reaction will occur until a state of dynamic equilibria is achieved, at which time the rate of forward reaction equals that of the reverse reaction, and so you see no observable change in the concentration of chemical species, that is, no further reaction occurs. We have used the concept of the reaction quotient to describe how your initial mixture relates to equilibrium. That is, if Q<K, products are formed (until Q=K), if Q>K, reactants are formed until Q=K, and of course, if Q=K, no reaction occurs. In this section we will look at systems at equilibrium, and see how they respond if they are perturbed from this equilibrium state. That is, Le Chatlier's principle states that if you have a system at equilibrium, and you then perturb it and induce a state of disequilibrium, the system will react in a manner that allows it to return to equilibrium.
This principle can be extended to non-chemical systems, like for example, the temperature of your home. If you like your room to be at a temperature of 70 deg F, and your system is perturbed by either a cold front or a heat wave occurring, you will react to return your equilibrium state by either turning on the heat, or the air conditioning respectively.
We need to remember that for a chemical system, equilibrium is attained when the forward rate equals the backward rate. So for the reaction
\[\begin{align} aA & \rightleftharpoons bB \\ R_{F} & = R_{B} \nonumber \;\;\; (at \; equlibrium)\\ \nonumber \\ k_{1}[A]^{m} & = k_{-1}[B]^{n} \;\;\; (at \; equlibrium) \end{align}\]
So there are two ways we can perturb a system at equilibrium, that is, make \(R_{f}\neq R_{b}\). The first is to change the concent of reactants or products so the rates don't equal, and the second is by changing the Temperature, which changes the value of k (\(k=Ae^{-\frac{E_a}{RT}}\)). If the system is a gaseous system, changes in pressure can change the concentration, and so general chemistry texts typically give three perturbations that you are expected to understand.
- \(\Delta\)[Concentration]
- \(\Delta\)P (for gaseous systems, which can change the concentration)
- \(\Delta\)T (this changes the value of k, and thus K, as \(K=\frac{k_f}{k_b}\)
Concentration
The concentration dependence is the easiest to understand. If you have a system, and then add something, the system will react to consume what you added, until equilibrium is achieved. On the other hand, if you have a system at equilibrium and you remove something, the system will produce what you removed until a new equilibrium is achieved. There is a virtual lab at the bottom of this page where you can change concentration of a reactant or product at equilibrium, causing a state of disequilibrium and allow you to observe how the system returns to equilibrium
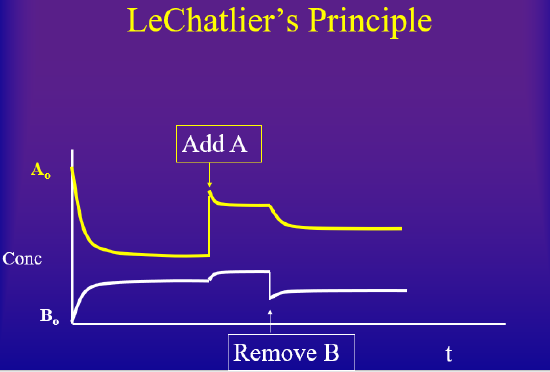
Pressure
There are two pressure effects. The first is adding or subtracting a single gas, and the second is changing the volume of a closed system, which changes the total pressure
Change Partial Pressure of a Single Gas
This is actually the same thing as changing the concentration of a species, and typically done by adding or removing a gas phase species. For gas A:
\[P_AV=n_ART\]
so
\[[A]=\frac{n_A}{V}=\frac{P_A}{RT}\]
Change in Total Pressure
If you change the volume of a closed system at constant temperature you change the total pressure according to Boyle's Law (PV=Constant), and so you change the concentration of all species. This will change the value of the the sum of the stoichiometric coefficients on the reactant side do not equal their sum on the product side.
- If you increase pressure by contracting the system the equilibrium will shift to the side with fewer species.
- If you decrease pressure by expanding the system the equilibrium will shift to the side with more species.
Case
Case \(\PageIndex{1}\):: Doubling the Volume (Halves the pressure)
Consider the formation of ammonia
\[N_2+3H_2 \rightleftharpoons 2NH_3\]
There are 4 species on the left, and two on the right,
(A) In what direction does the reaction proceed if we half the pressure by doubling the volume?
It moves the equilibrium to the left, creating more species.
Lets look at the math. initially we are at equilbrium
\[K=\frac{[NH_3]^2_{eq}}{[N_2]_{eq}[H_2]^3_{eq}}\nonumber\]
If we double the volume , then the new volumes are the initial divided by two and Q, the reaction quotient becomes:
\[ Q=\frac{\left (\frac{[NH_3]_{eq}}{2} \right )^2}{\left (\frac{[N_2]_{eq}}{2} \right )\left (\frac{[NH_3]_{eq}}{3} \right )^3}=\left (\frac{\left ( \frac{1}{2} \right )^2}{\left ( \frac{1}{2} \right )\left ( \frac{1}{2} \right )^3} \right )\left ( \frac{[NH_3]^2_{eq}}{[N_2]_{eq}[H_2]^3_{eq}} \right )=4K_{eq}\nonumber\]
That is, Q>K and it moves to the left as we predicted, forming reactants until Q=K.
Case \(\PageIndex{2}\): Halving the Volume (Doubles the pressure)
Consider the formation of ammonia
\[N_2+3H_2 \rightleftharpoons 2NH_3\]
There are 4 species on the left, and two on the right,
(A) In what direction does the reaction proceed if we double the pressure by halving the volume?
It moves the equilibrium to the right, reducing the total number of species.
Lets look at the math. initially we are at equilbrium
\[K=\frac{[NH_3]^2_{eq}}{[N_2]_{eq}[H_2]^3_{eq}}\nonumber\]
If we double the volume , then the new volumes are the initial divided by two and Q, the reaction quotient becomes:
\[ Q=\frac{\left(2[NH_3]_{eq} \right )^2}{\left(2[N_2]_{eq} \right )\left (2[H_2]_{eq} \right )^3}=\left (\frac{\left ( 2 \right )^2}{\left ( 2\right )\left ( 2 \right )^3} \right )\left ( \frac{[NH_3]^2_{eq}}{[N_2]_{eq}[H_2]^3_{eq}} \right )=\frac{1}{4}K_{eq}\nonumber\]
That is, Q<K and it moves to the right as we predicted, forming products until Q=K.
Change in Temperature
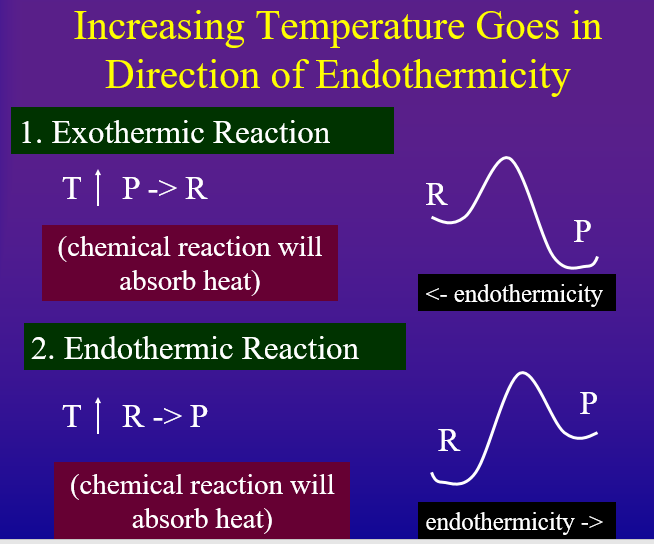
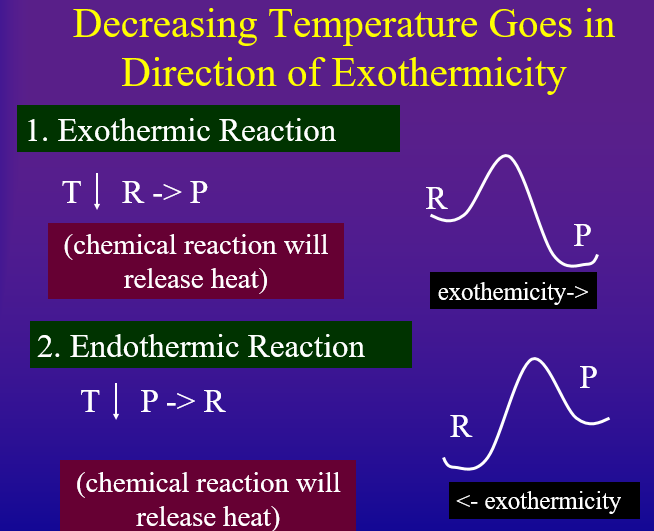
Every reaction has a direction of endothermicity and a direction of exothermicity. That is, an "endothermic reaction" is endothermic in the forward direction and exothermic in the reverse. Likewise, an "exothermic" reaction is exothermic in the forward direction, but endothermic in the reverse. According to Le Chatlier's principle if you add heat to the system, it will try and absorb it but going in the direction of endothermicity. On the other hand, if you remove heat from a system it will try and replace the heat by shifting in the direction of exothermicity.
- Increasing Temperature Shifts Equilibrium in Direction of Endothermicity to absorb heat added
- Decreasing Temperature Shifts Equilibrium in Direction of Exothermicity to replace heat removed
Probably the easiest way to look at this is to draw the Arrhenius diagram as in figures
Interactive Cobalt(II) Chloride(aq) Virtual Lab
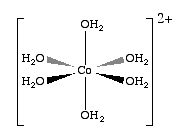
When the cobaltous cation (Co+2) dissolves in water it does not exist as a free ion, but forms a pink octahedral coordination complex with six water molecules, which is called hexaaquacobalt(II) ion, That is, the metal has empty d-orbitals of the cobalt ion accepts the lone pair electrons of a water molecules and forms a covalent bond, where both electrons come from the water. In fact six water molecules bond to each cobalt(II) cation, along the Cartesian axes, forming a pink octahedral complex (fig. *.*), which has the formula [Co(H2O)6]+2 . These are an important class of compounds as most metals form complexes with water, and this is a topic that was avoided in general chemistry 1. As we shall learn later this semester, coordination complexes are often highly colored, and thus easily observed. So in this virtual lab, we will take advantage of the color of coordination complexes to investigate Le Chatlier's principle. We can start by looking at a pink solution formed by the dissolution of cobalt (II) in water.
 |
|
| Aqueous \(Co^{+2}\) actually covalently bonds to 6 water molecules forming a pink \([Co(H_2O)_6]^{+2}) solution | |
In the presence of chloride a blue tetrahedral complex form, called tetrchlorocobalt(II) ion is formed
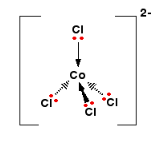 |
|
| Aqueous \(Co^{+2}\) actually covalently bonds to 6 water molecules forming a pink \([Co(H_2O)_6]^{+2}\) solution | |
The reaction of HCl and Co(aq) is thus described by the following equation and a good visual demonstration of Le Chatlier's principle as the solution is pink when reactant concentrations are high, and blue when product concentrations are high.
\[\underbrace{[Co(H_2O)_6]^{+2}(aq)}_{pink} + 4HCl(aq) \rightleftharpoons \underbrace{[Co(Cl)_2]^{-2}}_{blue} + 6H_2O +4H^+\]
| The equilibrium is also shifted by raising or lowering the temperature. On the left the blue solution was cooled and it turned pink. On the right the pink solution was heated and it turned blue. | |
In the virtual lab perform the following activities.
1.Note the color of 100 ml 1M CoCl2. At equilibrium, do you think K for pure CoCl2 favors reactants or products.
2. Predict how adding 12 M HCl would influence the equilibrium. Right click on the 100 ml 1M CoCl2 and duplicate, so you have two bottles. Now add 100 mL in 10 mL increments of 12M HCl to one of the bottles. Compare the two bottles.
3. Pour 100 ml of the blue solution into an empty 250 ml Erlenmeyer flask. Predict what would happen if you added silver nitrate, noting that silver reacts with chloride according the the following equation:
\[Ag^+(aq) + Cl^-(aq) \rightleftharpoons AgCl(s)\]
Add 100 mL in 10 mL increments of 6M AgNO3 to the blue flask containing 100 mL of the reaction solution.
4. Determine if the reaction is exothermic or endothermic by changing the temperature. Note, the virtual lab operates at an ambient temperature of 25oC. You can quickly change the temperature and isolate it from the surroundings by right clicking on a solution and choosing thermal properties. You then click "Insulated from surroundings" and type in the temperature you want.
\[\underbrace{[Co(H_2O)_6]^{+2}(aq)}_{pink} + 4HCl(aq) \rightleftharpoons \underbrace{[Co(Cl)_2]^{-2}}_{blue} + 6H_2O +4H^+\]
In Class Activity
Please click the following link, it should open the clicker question in a new page. Please return to this page once we after we have discussed the results


