2.10: Percent Composition
- Page ID
- 158412
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)learning objectives
- Calculate the mass percent composition of individual atoms in a compound
- Use the mass percent composition as a conversion factor to determine the mass of a component in a mixture and vice versa
- Use the mass percent composition as a conversion factor to determine the mass of a pure element in a compound and vice versa
Mass Percent Composition
Percent composition is very simple. Percent composition tells you by mass what percent of each element is present in a compound. A chemical compound is the combination of two or more elements. If you are studying a chemical compound, you may want to find the percent composition of a certain element within that chemical compound. The equation for percent composition is (mass of element/molecular mass) x 100. If you want to know the percent composition of the elements in an compound, follow these steps:
Steps to Solve:
- Find the molar mass of all the elements in the compound in grams per mole.
- Find the molecular mass of the entire compound.
- Divide the component's molar mass by the entire molecular mass.
- You will now have a number between 0 and 1. Multiply it by 100 to get percent composition!
Tips for solving:
- The compounds will always add up to 100%, so in a binary compound, you can find the % of the first element, then do 100%-(% first element) to get (% second element)
- If using a calculator, you can store the overall molar mass to a variable such as "A". This will speed up calculations, and reduce typographical errors.
These steps are outlined in the figure below.

For another example, if you wanted to know the percent composition of hydrochloric acid (HCl), first find the molar mass of Hydrogen. H = 1.00794g. Now find the molecular mass of HCl: 1.00794g + 35.4527g = 36.46064g. Follow steps 3 and 4: (1.00794g/36.46064g) x 100 = 2.76% Now just subtract to find the percent by mass of Chlorine in the compound: 100%-2.76% = 97.24% Therefore, HCl is 2.76% Hydrogen and 97.24% Chlorine by mass.
Percent Composition in Everyday Life
Percent composition plays an important role in everyday life. It is more than just the amount of chlorine in your swimming pool because it concerns everything from the money in your pocket to your health and how you live. The next two sections describe percent composition as it relates to you.
Nutrition Labels
The nutrition label found on the container of every bit of processed food sold by the local grocery store employs the idea of percent composition. On all nutrition labels, a known serving size is broken down in five categories: Total Fat, Cholesterol, Sodium, Total Carbohydrate, and Protein. These categories are broken down into further subcategories, including Saturated Fat and Dietary Fiber. The mass for each category, except Protein, is then converted to percent of Daily Value. Only two subcategories, Saturated Fat and Dietary Fiber are converted to percent of Daily Value. The Daily Value is based on a the mass of each category recommended per day per person for a 2000 calorie diet. The mass of protein is not converted to percent because their is no recommended daily value for protein. Following is a picture outlining these ideas.
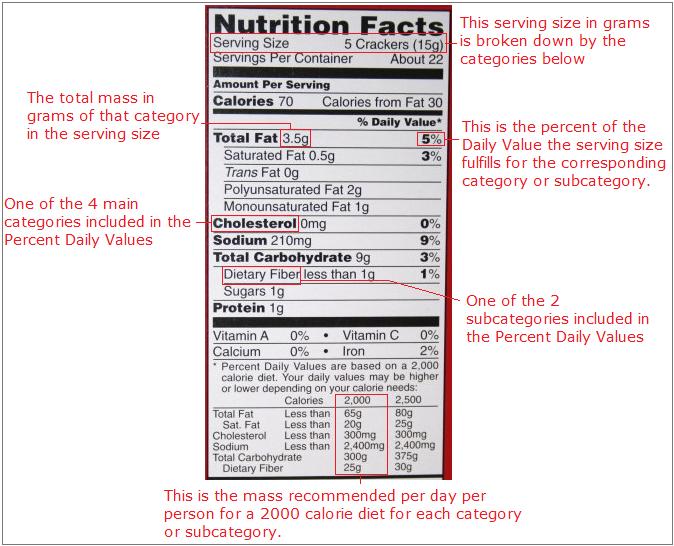
For example, if you wanted to know the percent by mass of the daily value for sodium you are eating when you eat one serving of the food with this nutrition label, then go to the category marked sodium. Look across the same row and read the percent written. If you eat one serving of this food, then you will have consumed about 9% of your daily recommended value for sodium. To find the percent mass of fat in the whole food, you could divide 3.5 grams by 15 grams, and see that this snack is 23.33% fat.
Penny: The Lucky Copper Coin
The penny should be called "the lucky copper coated coin." The penny has not been made of solid copper since part of 1857. After 1857, the US government started adding other cheaper metals to the mix. The penny, being only one cent, is literally not worth its weight in copper. People could melt copper pennies and sell the copper for more than the pennies were worth. After 1857, nickel was mixed with the more expensive copper. After 1864, the penny was made of bronze. Bronze is 95% copper and 5% zinc and tin. For one year, 1943, the penny had no copper in it due to the expense of the World War II. It was just zinc coated steel. After 1943 until 1982, the penny went through periods where it was brass or bronze.

Today, the penny in America is 2.5% copper with 97.5% zinc. The copper coats the outside of the penny while the inner portion is zinc. For comparison's sake, the penny in Canada is 94% steel, 1.5% nickel, and 4.5% copper.
The percent composition of a penny may actually affect health, particularly the health of small children and pets. Since the newer pennies are made mainly of zinc instead of copper, they are a danger to a child's health if ingested. Zinc is very susceptible to acid. If the thin copper coating is scratched and the hydrochloric acid present in the stomach comes into contact with the zinc core it could cause ulcers, anemia, kidney and liver damage, or even death in severe cases. Three important factors in penny ingestion are time, pH of the stomach, and amount of pennies ingested. Of course, the more pennies swallowed, the more danger of an overdose of zinc. The more acidic the environment, the more zinc will be released in less time. This zinc is then absorbed and sent to the liver where it begins to cause damage. In this kind of situation, time is of the essence. The faster the penny is removed, the less zinc is absorbed. If the penny or pennies are not removed, organ failure and death can occur.
Below is a picture of a scratched penny before and after it had been submerged in lemon juice. Lemon juice has a similar pH of 1.5-2.5 when compared to the normal human stomach after food has been consumed. Time elapsed: 36 hours.


As you can see, the copper is vastly unharmed by the lemon juice. That's why pennies made before 1982 with mainly copper (except the 1943 penny) are relatively safe to swallow. Chances are they would pass through the digestive system naturally before any damage could be done. Yet, it is clear that the zinc was partially dissolved even though it was in the lemon juice for only a limited amount of time. Therefore, the percent composition of post 1982 pennies is hazardous to your health and the health of your pets if ingested. To learn more about acids and bases, check here: wiki.
Video tutor: Percent Composition of Acetic Acid
video tutor: Percent Composition of Acetylene and Benzene
Note: Acetylene and Benzene have the same Percent Composition as each other, however this does not mean that they are the same substance.
Example \(\PageIndex{1}\)
The mass of one penny is 2.5 grams. How many pennies can the U.S. government make with 20.0 Kg of copper if the mass percent composition of a copper in the modern penny is 2.5%?
Given: We know that we are starting with 20.0 Kg of pure copper. We know the mass percent composition of pure copper in the penny mixture. We also know the mass of each penny.
Strategy: We need to figure out the mass of copper mixture we can make with 20.0 Kg of pure copper using the mass percent composition of the copper in the penny mixture. From there we can determine how many individual pennies we can make with this mixture.
Solution
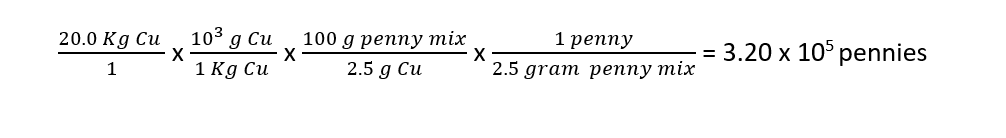
Example \(\PageIndex{2}\)
What is the mass of carbon contained in 3.0 g of butane (C4H10), lighter fluid?
Given: the mass of the whole (butane), what is the mass of the part (carbon)?
Strategy: use the mass percent composition formulas to convert from mass of butane to mass of carbon:
Solution

Practice: Percent Composition Problems
These problems will follow the same pattern of difficulty as those of density.
- Calculate the percent by mass of each element in Cesium Fluoride (CsF).
- Calculate the percent by mass of each element present in carbon tetrachloride (CCl4)
- A solution of salt and water is 33.0% salt by mass and has a density of 1.50 g/mL. What mass of the salt in grams is in 5.00L of this solution?
- A solution of water and HCl contains 25% HCl by mass. The density of the solution is 1.05 g/mL. If you need 1.7g of HCl for a reaction, what volume of this solution will you use?
- A solution containing 42% NaOH by mass has a density of 1.30 g/mL. What mass, in kilograms, of NaOH is in 6.00 L of this solution?
EXTRA GAS PROBLEM ATTACHED BELOW
Percent Composition Problem Solutions
1) CsF is 87.5% Cs and 12.5% F by mass
2) CCl4is 92.2% Cl and 7.8% C by mass
3) 2480g
4) 6.5mL
5) 2.38 kg
References
- AUTOR , ARQUIMEDES , and Thomas Little . The Works of Archimedes . Courier Dover Publications, 2002.
- Chande, D. and T. Fisher (2003). "Have a Penny? Need a Penny? Eliminating the One-Cent Coin from Circulation." Canadian Public Policy/Analyse de Politiques 29(4): 511-517.
-
Jefferson, T. (1999). "A Thought for Your Pennies." JAMA 281(2): 122.
- Petrucci , Ralph , William Harwood , and Geoffrey Herring . Principles and Modern Application. ninth . New Jersey : Peason Eduation , 2007.
-
Rauch, F., H. Plotkin, et al. (2003). "Bone Mass, Size, and Density in Children and Adolescents with Osteogenesis Imperfecta: Effect of Intravenous Pamidronate Therapy." Journal of Bone and Mineral Research 18: 610-614.
-
Richardson, J., S. Gwaltney-Brant, et al. (2002). "Zinc Toxicosis from Penny Ingestion in Dogs." Vet Med 97(2): 96-99.
-
Tate, J. "Archimedes’ Discoveries: A Closer Look."
Outside Links
- http://en.wikipedia.org/wiki/Density
- http://www.sparknotes.com/testprep/b...section2.rhtml
- http://www.science.co.il/PTelements.asp
Contributors
- Content borrowed from: 2.13: Percent Composition
- Bob Belford (UA of Little Rock)
- Modified by Ronia Kattoum (UA of Little Rock)

