6.1: Electromagnetic Radiation
- Page ID
- 52777
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Describe the characteristics of light and how it relates to matter
- Define electromagnetic radiation and give examples of electromagnetic radiation
- Differentiate between transverse and compressional waves
- Relate the wavelength and frequency of a electromagnetic radiation to the speed of light
- Rank the various types of electromagnetic radiation in order of increasing/decreasing frequency and wavelength
Introduction
Light interacts with matter, and it is through studying this interaction that scientists have learned a lot of what they know about the structure of matter. Light is electromagnetic radiation, and the nature of the interaction of light and matter is influenced by the energy of the light. For example, light of the proper energy can cause an electron to move from one orbital to another that has a different energy. There are two basic process, absorption and emission.
- Absorption: This is an endothermic process where matter absorbs the light energy.
- Emission: This is an exothermic process where light energy is emitted, and leaves the system (matter).
What are some characteristics of light?
- Light travels through space.
- Light has color.
- Light has energy.
- Light energy is quantified.
What is Light?
Light is electromagnetic radiation, which travels through space in light waves.
Properties of Waves
There are two basic types of waves, transverse and compressional. A transverse wave induces periodic oscillation perpendicular to the direction of the wave front, like a wave traveling across the surface of water causes an object to oscillate up and down. Light waves (electromagnetic radiation) are transverse waves. Compressional or longitudinal waves cause oscillating motion along the direction of the wavefront, where the particle density oscillates as they are compressed and expanded. Acoustic waves are longitudinal, as indicated by the vibrating speaker.
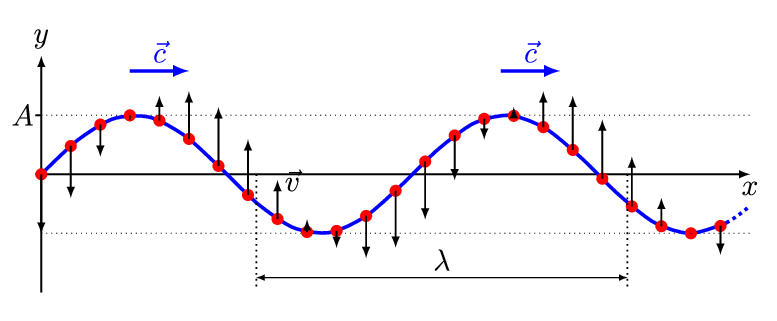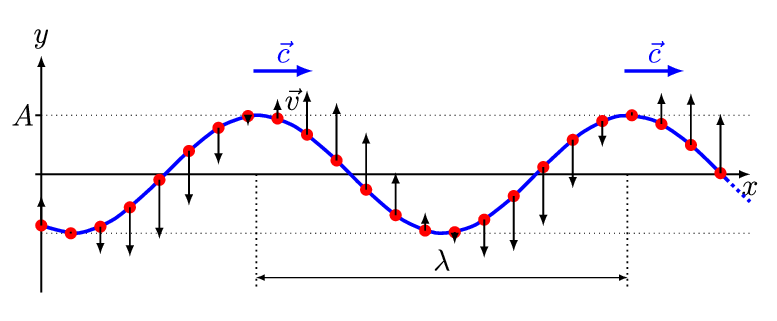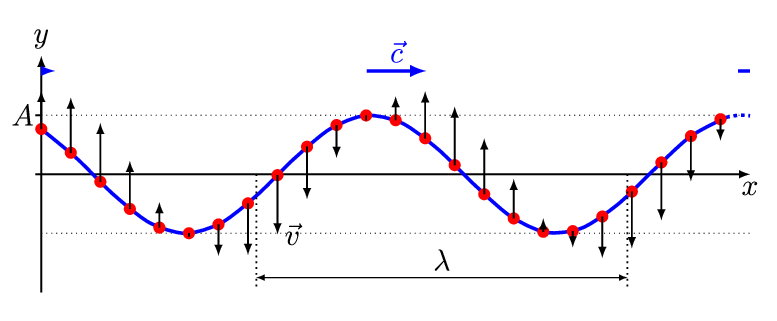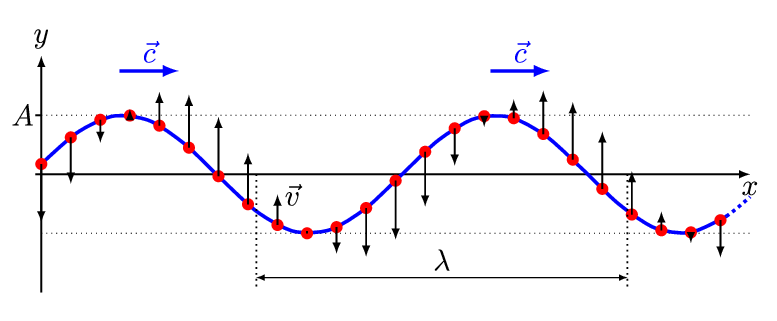
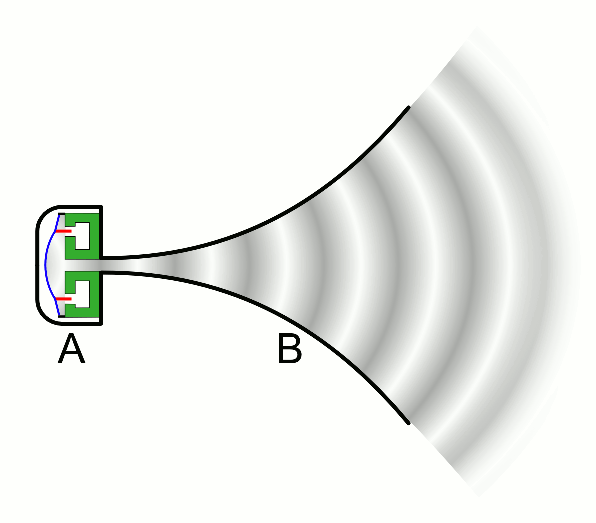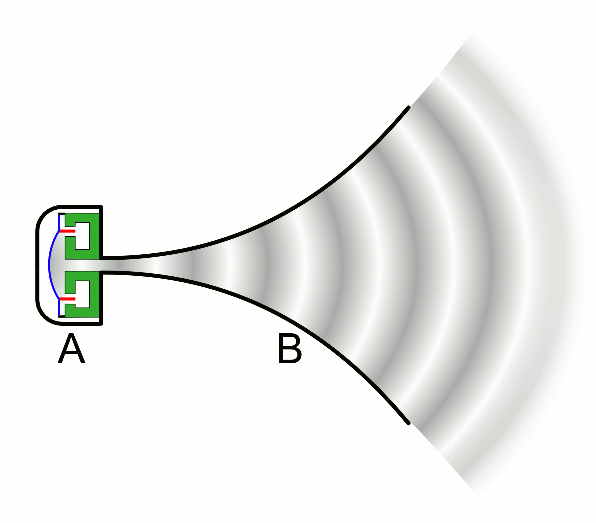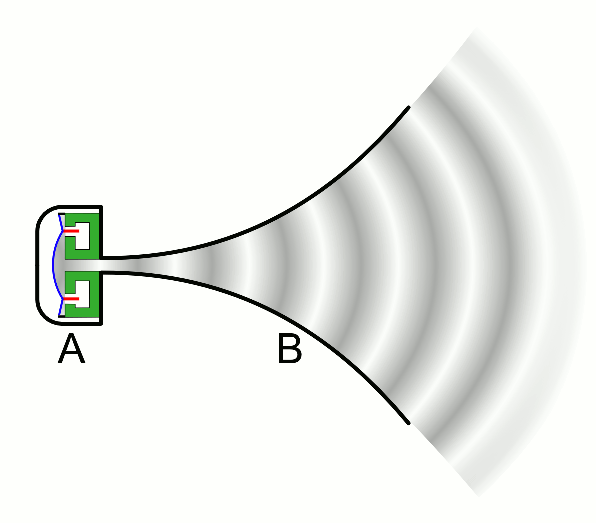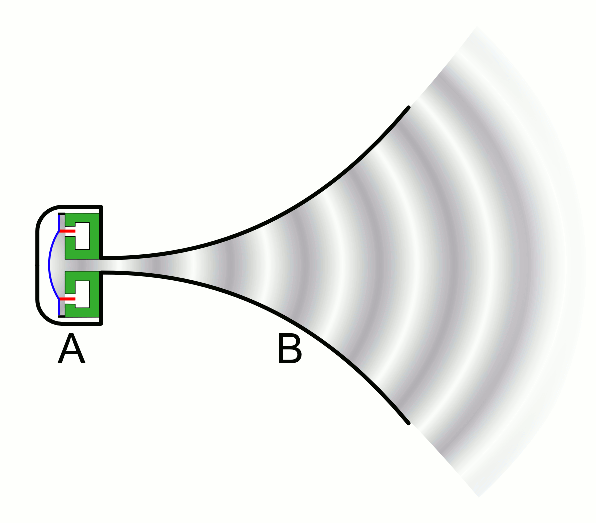
Figure \(\PageIndex{1}\): Animated Gifs of transverse and longitudinal waves. Light waves are transverse waves while acoustic are longitudinal.
Wave Properties for Transverse Waves
- Amplitude- maximum displacement from undisturbed position during a complete oscillation, (units depend on what is oscillating).
- Wavelength ( \(\lambda\)) -The distance between two peaks (units of length,typically nm for visible light).
- Frequency (\(\nu\))- Oscillations per unit of time (Hertz is cycles per second, and has units of sec-1, your AC house electricity is 60Hz, meaning the frequency of oscillation is 60 times a second).
- Wave Speed - how fast the wave front propagates through the medium (units of distance per time). Use c for light waves.
\[\begin{align} \text{Wave Speed} & = \lambda \nu \nonumber \\ & =\text{(wavelenth)(frequency)} \end{align} \]
Electromagnetic Radiation
Light travels through space as an oscillation of electric and magnetic fields that are orthogonal (at right angles) to each other and the direction of propagation. So there are three vectors associated with a light beam, each that could be described by a Cartesian coordinate system axis. If the light in Figure 6.1.2 moves in the direction of the Z-axis, that would be the direction of the propagation and it is moving at the speed of light. (Note, speed is a scalar, how fast something moves, but does not tell you in what direction. Velocity is a vector, and tells you both the speed and direction of motion). This motion would then induce concurrent oscillations of an Electric Field along the X-axis and the magnetic field along the Y-axis, but osciallating in phase and at the same frequency.
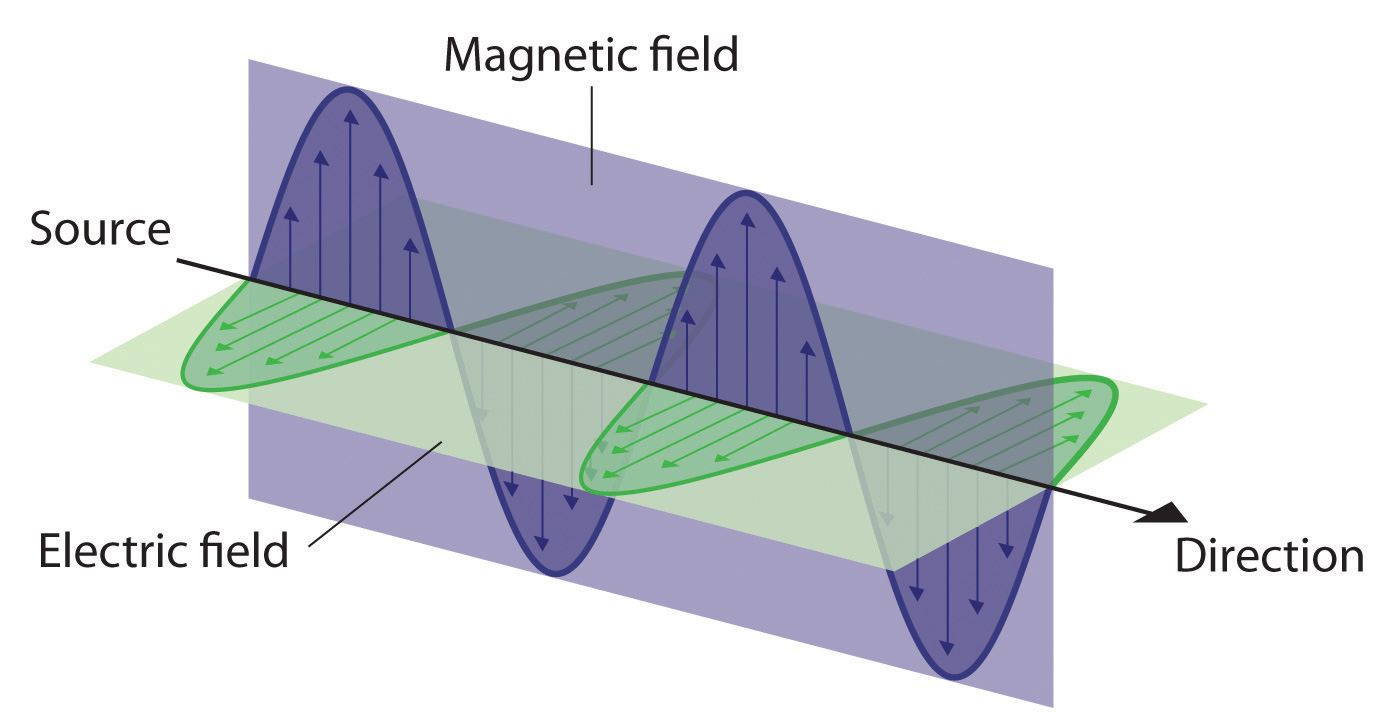
As the above video show clearly shows, in today's modern world we are surrounded by electromagnetic energy coming from devices of anthropogenic origins.
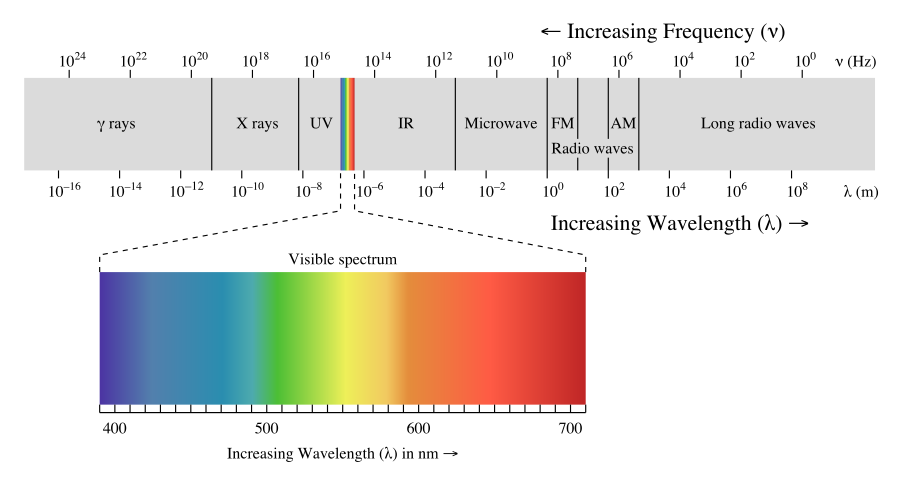
The Electromagnetic spectrum
The electromagnetic spectrum describes light across a range of frequencies. Video 6.1.1 gives a good feel for the types of applications the different regions of the spectrum are used for. In the next section we discuss energy, and the higher the frequency (the lower the wavelength), the higher the energy.
Exercise \(\PageIndex{1}\)
Is the wavelength of the UV radiation longer or shorter than microwaves?
- Answer
-
Shorter. Gamma radiation has the shortest wavelength (greatest frequency). As you move from gamma rays to radio waves, the wavelength increases and frequency decreases.
Properties of Electromagnetic Radiation
\[c=\lambda \nu \label{6.2.1}\]
- c= 3.00 ×108 m/s (2.99792458 × 108 m/s), which is 1.86 × 105 mi/s and about a million times faster than the speed of sound.
- \(\lambda\) - Wavelength, unit depends on the part of the Electromagnetic Spectrum you are interested in. Typically use SI prefixes and meters, so that the number is between 1 and 999. So in the visible region, we would use nm, with the range roughly being between 400 and 400 nm.
- \(\nu\)- Frequency (Hz, or cycles per second)
Example \(\PageIndex{1}\)
A sodium streetlight gives off yellow light that has a wavelength of 589 nm (\(1 nm = 1 \times 10^{−9} m\)). What is the frequency of this light?
Solution
We can rearrange the Equation \ref{6.2.1} to solve for the frequency:
\[ v=\dfrac{c}{λ} \nonumber\]
Since \(c\) is expressed in meters per second, we must also convert 589 nm to meters.
\[ v=\mathrm{\left(\dfrac{2.998×10^8\:\cancel{m}s^{−1}}{589\cancel{nm}}\right)\left(\dfrac{1×10^9\cancel{nm}}{1\cancel{m}}\right)=5.09×10^{14}\,s^{−1}} \nonumber\]
Exercise \(\PageIndex{2}\)
One of the frequencies used to transmit and receive cellular telephone signals in the United States is 850 MHz. What is the wavelength in meters of these radio waves?
- Answer
-
0.353 m = 35.3 cm
Exercise \(\PageIndex{3}\)
What is the frequency of a wave with a wavelength of 500 pm?
- Answer
-
\(6.0 \times 10^{17}\, Hz\)
Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
- Ronia Kattoum (UALR)
- Paul Flowers, et al. Open Stax (examples and exercises)
- anonymous


