1A.8: Energy: Some Basic Principles
- Page ID
- 50458
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Define energy and differentiate between kinetic and potential energy
- Define chemical and thermal energy
- Differentiate between heat and work
What is Energy?
Energy is one of the most fundamental and universal concepts of physical science, but one that is remarkably difficult to define in a way that is meaningful to most people. This perhaps reflects the fact that energy is not a “thing” that exists by itself, but is rather an attribute of matter (and also of electromagnetic radiation) that can manifest itself in different ways. It can be observed and measured only indirectly through its effects on matter that acquires, loses, or possesses it.
The concept that we call energy was very slow to develop; it took more than a hundred years just to get people to agree on the definitions of many of the terms we use to describe energy and the interconversion between its various forms. But even now, most people have some difficulty in explaining what it is; somehow, the definition we all learned in elementary science ("the capacity to do work") seems less than adequate to convey its meaning.
Although the term "energy" was not used in science prior to 1802, it had long been suggested that certain properties related to the motions of objects exhibit an endurance which is incorporated into the modern concept of "conservation of energy". In the 17th Century, the great mathematician Gottfried Leibnitz (1646-1716) suggested the distinction between vis viva ("live force") and vis mortua ("dead force"), which later became known as kinetic energy (1829) and potential energy (1853).
Kinetic energy and potential energy
Whatever energy may be, there are basically two kinds.
Kinetic energy is associated with the motion of an object, and its direct consequences are part of everyone's daily experience; the faster the ball you catch in your hand, and the heavier it is, the more you feel it. Quantitatively, a body with a mass m and moving at a velocity v possesses the kinetic energy mv2/2.
Example \(\PageIndex{1}\)
A rifle shoots a 4.25 g bullet at a velocity of 965 m s–1. What is its kinetic energy?
Solution
The only additional information you need here is that
1 J = 1 kg m2 s–2:
KE = ½ × (.00425 kg) (965 m s–1)2 = 1980 J
Potential energy is energy a body has by virtue of its location. But there is more: the body must be subject to a "restoring force" of some kind that tends to move it to a location of lower potential energy. Think of an arrow that is subjected to the force from a stretched bowstring; the more tightly the arrow is pulled back against the string, the more potential energy it has.
More generally, the restoring force comes from what we call a force field— a gravitational, electrostatic, or magnetic field. We observe the consequences of gravitational potential energy all the time, such as when we walk, but seldom give it any thought.
If an object of mass m is raised off the floor to a height h, its potential energy increases by mgh, where g is a proportionality constant known as the acceleration of gravity; its value at the earth's surface is 9.8 m s–2.
Example \(\PageIndex{2}\)
Find the change in potential energy of a 2.6 kg textbook that falls from the 66-cm height of a table top onto the floor.
Solution
PE = m g h = (2.6 kg)(9.8 m s–2)(0.66 m) = 16.8 kg m2 s–2 = 16.8 J
Similarly, the potential energy of a particle having an electric charge qdepends on its location in an electrostatic field.
"Chemical energy"
Electrostatic potential energy plays a major role in chemistry; the potential energies of electrons in the force field created by atomic nuclei lie at the heart of the chemical behavior of atoms and molecules. "Chemical energy" usually refers to the energy that is stored in the chemical bonds of molecules. These bonds form when electrons are able to respond to the force fields created by two or more atomic nuclei, so they can be regarded as manifestations of electrostatic potential energy. In an exothermic chemical reaction, the electrons and nuclei within the reactants undergo rearrangement into products possessing lower energies, and the difference is released to the environment in the form of heat.
Interconversion of potential and kinetic energy
Transitions between potential and kinetic energy are such an intimate part of our daily lives that we hardly give them a thought. It happens in walking as the body moves up and down. Our bodies utilize the chemical energy in glucose to keep us warm and to move our muscles. In fact, life itself depends on the conversion of chemical energy to other forms.
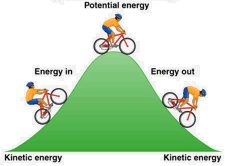
Energy is conserved: it can neither be created nor destroyed. So when you go uphill, your kinetic energy is transformed into potential energy, which gets changed back into kinetic energy as you coast down the other side. And where did the kinetic energy you expended in peddling uphill come from? By conversion of some of the chemical potential energy in your breakfast cereal.
Thermal energy
Kinetic energy is associated with motion, but in two different ways. For a macroscopic object such as a book or a ball, or a parcel of flowing water, it is simply given by ½ mv2. However, when an object is dropped onto the floor, or when an exothermic chemical reaction heats surrounding matter, the kinetic energy gets dispersed into the molecular units in the environment. This "microscopic" form of kinetic energy, unlike that of a speeding bullet, is completely random in the kinds of motions it exhibits and in its direction. We refer to this as "thermalized" kinetic energy, or more commonly simply as thermal energy. We observe the effects of this as a rise in the temperature of the surroundings, or a phase change (like melting). The temperature of a body is direct measure of the quantity of thermal energy is contains.
Energy units
Energy is measured in terms of its ability to perform work or to transfer heat. Mechanical work is done when a force f displaces an object by a distance d:
\[w = f × d\]
The basic unit of energy is the joule. One joule is the amount of work done when a force of 1 newton acts over a distance of 1 m; thus 1 J = 1 N-m. The newton is the amount of force required to accelerate a 1-kg mass by 1 m/sec2, so the basic dimensions of the joule are kg m2 s–2. The other two units in wide use. the calorie and the BTU (British thermal unit) are defined in terms of the heating effect on water. Because of the many forms that energy can take, there are a correspondingly large number of units in which it can be expressed, a few of which are summarized below.
Heat and Work
Heat and work are both measured in energy units, so they must both represent energy. How do they differ from each other, and from just plain “energy” itself? In our daily language, we often say that "this object contains a lot of heat", but this is gibberish in thermodynamics terms, although it is ok to say that the object is "hot", indicating that its temperature is high. The term "heat" has a special meaning in thermodynamics: it is a process in which a body (the contents of a tea kettle, for example) acquires or loses energy as a direct consequence of its having a different temperature than its surroundings. Hence, thermal energy can only flow from a higher temperature to a lower temperature. It is this flow that constitutes "heat". Use of the term "flow" of heat recalls the incorrect 18th-century notion that heat is an actual substance called “caloric” that could flow like a liquid.
Test Yourself
Query \(\PageIndex{1}\)
Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
- modified from
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook
- Ronia Kattoum (Learning Objectives)
- Elena Lisitsyna (H5P interactive modules)


