5.E: Exercises

5.1: The Nature of Energy

Conceptual Problems

1. What is the relationship between mechanical work and energy?

2. Does a person with a mass of 50 kg climbing a height of 15 m do work? Explain your answer. Does that same person do work while descending a mountain?

3. If a person exerts a force on an immovable object, does that person do work? Explain your answer.

4. Explain the differences between electrical energy, nuclear energy, and chemical energy.

5. The chapter describes thermal energy, radiant energy, electrical energy, nuclear energy, and chemical energy. Which form(s) of energy are represented by each of the following?

   1. sunlight
   2. the energy produced by a cathode ray tube, such as that found in a television
   3. the energy emitted from radioactivity
   4. the energy emitted from a burning candle
   5. the energy associated with a steam engine
   6. the energy emitted by a cellular phone
   7. the energy associated with a stick of dynamite

6. Describe the various forms of energy that are interconverted when a flashlight is switched on.

7. Describe the forms of energy that are interconverted when the space shuttle lifts off.

8. Categorize each of the following as representing kinetic energy or potential energy.

   1. the energy associated with a laptop computer sitting on the edge of a desk
   2. shoveling snow
   3. water pouring out of a fire hydrant
   4. the energy released by an earthquake
   5. the energy in a volcano about to erupt
   6. the energy associated with a coiled spring

9. Are the units for potential energy the same as the units for kinetic energy? Can an absolute value for potential energy be obtained? Explain your answer.

10. Categorize each of the following as representing kinetic energy or potential energy.

    1. water cascading over Niagara Falls
    2. a beaker balanced on the edge of a sink
    3. the energy released during a mudslide
    4. rollerblading
    5. the energy in a block of ice on a rooftop before a thaw

11. Why does hammering a piece of sheet metal cause the metal to heat up?

Conceptual Answers

3. Technically, the person is not doing any work, since the object does not move.

11. he kinetic energy of the hammer is transferred to the metal.

Numerical Problems

Please be sure you are familiar with the topics discussed in Essential Skills 4 before proceeding to the Numerical Problems.

1. Describe the mathematical relationship between (a) the thermal energy stored in an object and that object’s mass and (b) the thermal energy stored in an object and that object’s temperature.

2. How much energy (in kilojoules) is released or stored when each of the following occurs?

   1. A 230 lb football player is lifted to a height of 4.00 ft.
   2. An 11.8 lb cat jumps from a height of 6.50 ft.
   3. A 3.75 lb book falls off of a shelf that is 5.50 ft high.

3. Calculate how much energy (in kilojoules) is released or stored when each of the following occurs:

   1. A 130 lb ice skater is lifted 7.50 ft off the ice.
   2. A 48 lb child jumps from a height of 4.0 ft.
   3. An 18.5 lb light fixture falls from a 10.0 ft ceiling.

4. A car weighing 1438 kg falls off a bridge that is 211 ft high. Ignoring air resistance, how much energy is released when the car hits the water?

5. A 1 tn roller coaster filled with passengers reaches a height of 28 m before accelerating downhill. How much energy is released when the roller coaster reaches the bottom of the hill? Assume no energy is lost due to friction.

Numerical Answers

1.

1. The thermal energy content of an object is directly proportional to its mass.
2. The thermal energy content of an object is directly proportional to its temperature.

3.

1. 1.3 kJ stored
2. 0.26 kJ released
3. 0.251 kJ released

5.

1. 250 kJ released

5.2: The First Law of Thermodynamics

---

Conceptual Problems

1. Describe how a swinging pendulum that slows with time illustrates the first law of thermodynamics.
2. When air is pumped into a bicycle tire, the air is compressed. Assuming that the volume is constant, express the change in internal energy in terms of q and w.
3. What is the relationship between enthalpy and internal energy for a reaction that occurs at constant pressure?
4. An intrepid scientist placed an unknown salt in a small amount of water. All the salt dissolved in the water, and the temperature of the solution dropped several degrees.

1. What is the sign of the enthalpy change for this reaction?
2. Assuming the heat capacity of the solution is the same as that of pure water, how would the scientist calculate the molar enthalpy change?
3. Propose an explanation for the decrease in temperature.

5. For years, chemists and physicists focused on enthalpy changes as a way to measure the spontaneity of a reaction. What arguments would you use to convince them not to use this method?

6. What is the relationship between enthalpy and internal energy for a reaction that occurs at constant volume?

7. The enthalpy of combustion (ΔH_comb) is defined thermodynamically as the enthalpy change for complete oxidation. The complete oxidation of hydrocarbons is represented by the following general equation: hydrocarbon + O₂(g) → CO₂(g) + H₂O(g). Enthalpies of combustion from reactions like this one can be measured experimentally with a high degree of precision. It has been found that the less stable the reactant, the more heat is evolved, so the more negative the value of ΔHcomb. In each pair of hydrocarbons, which member do you expect to have the greater (more negative) heat of combustion? Justify your answers.

1. cyclopropane or cyclopentane
2. butane or 2-methylpropane
3. hexane or cyclohexane

8. Using a structural argument, explain why the trans isomer of 2-butene is more stable than the cis isomer. The enthalpies of formation of cis- and trans-2-butene are −7.1 kJ/mol and −11.4 kJ/mol, respectively.

9. Using structural arguments, explain why cyclopropane has a positive ΔH_f° (12.7 kJ/mol), whereas cyclopentane has a negative ΔH_f° (−18.4 kJ/mol). (Hint: consider bond angles.)

Conceptual Answers

3. At constant pressure, ΔH = ΔE + PΔV.
4. Video Solution

5. In some simple case, when a reaction only involves solids, liquids or liquid solution, we can say that \(ΔH=ΔE\). When a reaction involves gases, we can say that \(ΔE = ΔH − RTΔn\). However, if we have a complicated case, it is hard to use \(ΔH\) to measure the spontaneity of a reaction. For example, when a reaction involved gases, liquid and solid, it is really hard for us to defined \(Δ(PV)\).

9. With bond angles of 60°, cyclopropane is highly strained, causing it to be less stable than cyclopentane, which has nearly ideal tetrahedral geometry at each carbon atom.

Numerical Problems

1. A block of CO₂ weighing 15 g evaporates in a 5.0 L container at 25°C. How much work has been done if the gas is allowed to expand against an external pressure of 0.98 atm under isothermal conditions? The enthalpy of sublimation of CO₂ is 25.1 kJ/mol. What is the change in internal energy (kJ/mol) for the sublimation of CO₂ under these conditions?
2. Zinc and HCl react according to the following equation:

\[Zn_{(s)} + 2HCl_{(aq)} \rightarrow Zn^{2+}_{(aq)} + 2Cl^−_{(aq)} + H_2(g)\]

When 3.00 g of zinc metal is added to a dilute HCl solution at 1.00 atm and 25°C, and this reaction is allowed to go to completion at constant pressure, 6.99 kJ of heat must be removed to return the final solution to its original temperature. What are the values of q and w, and what is the change in internal energy?

3. Acetylene torches, used industrially to cut and weld metals, reach flame temperatures as high as 3000°C. The combustion reaction is as follows:

\[2C_2H_{2\; (g)}+5O_{2\; (g)} \rightarrow 4CO_{2\; (g)} + 2H_2O_{(l)} \tag{ΔH=−2599 kJ}\]

Calculate the amount of work done against a pressure of 1.0 atm when 4.0 mol of acetylene are allowed to react with 10 mol of O₂ at 1.0 atm at 20°C. What is the change in internal energy for the reaction?

4. When iron dissolves in 1.00 M aqueous HCl, the products are FeCl₂(aq) and hydrogen gas. Calculate the work done if 30 g of Fe react with excess hydrochloric acid in a closed vessel at 20°C. How much work is done if the reaction takes place in an open vessel with an external pressure of 1.0 atm?

Numerical Answers

1. −350 J; 8.2 kJ

5.3: Enthalpy

---

5.4: Enthalpy of Reaction

---

Conceptual Problems

Please be sure you are familiar with the topics discussed in Essential Skills 4 (Section 5.6 "Essential Skills 4") before proceeding to the Conceptual Problems.

1. Heat implies the flow of energy from one object to another. Describe the energy flow in an

   a. exothermic reaction.

   b. endothermic reaction.

2. When a thermometer is suspended in an insulated thermos that contains a block of ice, the temperature recorded on the thermometer drops. Describe the direction of heat flow.

3. In each scenario, the system is defined as the mixture of chemical substances that undergoes a reaction. State whether each process is endothermic or exothermic.

   1. Water is added to sodium hydroxide pellets, and the flask becomes hot.
   2. The body metabolizes glucose, producing carbon dioxide and water.
   3. Ammonium nitrate crystals are dissolved in water, causing the solution to become cool.

4. In each scenario, the system is defined as the mixture of chemical substances that undergoes a reaction. Determine whether each process is endothermic or exothermic.

   1. Concentrated acid is added to water in a flask, and the flask becomes warm.
   2. Water evaporates from your skin, causing you to shiver.
   3. A container of ammonium nitrate detonates.

5. Is Earth’s environment an isolated system, an open system, or a closed system? Explain your answer.

6. Why is it impossible to measure the absolute magnitude of the enthalpy of an object or a compound?

7. Determine whether energy is consumed or released in each scenario. Explain your reasoning.

   1. A leaf falls from a tree.
   2. A motorboat maneuvers against a current.
   3. A child jumps rope.
   4. Dynamite detonates.
   5. A jogger sprints down a hill.

8. The chapter states that enthalpy is an extensive property. Why? Describe a situation that illustrates this fact.

9. The enthalpy of a system is affected by the physical states of the reactants and the products. Explain why.

10. Is the distance a person travels on a trip a state function? Why or why not?

5.5: Calorimetry

---

Conceptual Problems

1. Can an object have a negative heat capacity? Why or why not?
2. What two factors determine the heat capacity of an object? Does the specific heat also depend on these two factors? Explain your answer.
3. Explain why regions along seacoasts have a more moderate climate than inland regions do.
4. Although soapstone is more expensive than brick, soapstone is frequently the building material of choice for fireplaces, particularly in northern climates with harsh winters. Propose an explanation for this.

Numerical Problems

Please be sure you are familiar with the topics discussed in Essential Skills 4 (Section 9.9) before proceeding to the Numerical Problems.

1. Using Equation 9.6.2 and Equation 9.6.3, derive a mathematical relationship between C_s and C_p.

2. Complete the following table for 28.0 g of each element at an initial temperature of 22.0°C.

   Element	q (J)	Cp [J/(mol·K)]	Final T (°C)
   nickel	137	26.07
   silicon		19.789	3.0
   zinc	603		77.5
   mercury	137		57

3. Using Table 9.6.1, how much heat is needed to raise the temperature of a 2.5 g piece of copper wire from 20°C to 80°C? How much heat is needed to increase the temperature of an equivalent mass of aluminum by the same amount? If you were using one of these metals to channel heat away from electrical components, which metal would you use? Once heated, which metal will cool faster? Give the specific heat for each metal.

4. Gold has a molar heat capacity of 25.418 J/(mol·K), and silver has a molar heat capacity of 23.350 J/(mol·K).

   1. If you put silver and gold spoons of equal mass into a cup of hot liquid and wait until the temperature of the liquid is constant, which spoon will take longer to cool down when removed from the hot liquid?
   2. If 8.00 g spoons of each metal at 20.0°C are placed in an insulated mug with 50.0 g of water at 97.0°C, what will be the final temperature of the water after the system has equilibrated? (Assume that no heat is transferred to the surroundings.)

5. In an exothermic reaction, how much heat would need to be evolved to raise the temperature of 150 mL of water 7.5°C? Explain how this process illustrates the law of conservation of energy.

6. How much heat must be evolved by a reaction to raise the temperature of 8.0 oz of water 5.0°C? What mass of lithium iodide would need to be dissolved in this volume of water to produce this temperature change?

7. A solution is made by dissolving 3.35 g of an unknown salt in 150 mL of water, and the temperature of the water rises 3.0°C. The addition of a silver nitrate solution results in a precipitate. Assuming that the heat capacity of the solution is the same as that of pure water, use the information in Table 9.5.1 and solubility rules to identify the salt.

8. Using the data in Table 9.8.2, calculate the change in temperature of a calorimeter with a heat capacity of 1.78 kJ/°C when 3.0 g of charcoal is burned in the calorimeter. If the calorimeter is in a 2 L bath of water at an initial temperature of 21.5°C, what will be the final temperature of the water after the combustion reaction (assuming no heat is lost to the surroundings)?

9. A 3.00 g sample of TNT (trinitrotoluene, C₇H₅N₃O₆) is placed in a bomb calorimeter with a heat capacity of 1.93 kJ/°C; the ΔH_comb of TNT is −3403.5 kJ/mol. If the initial temperature of the calorimeter is 19.8°C, what will be the final temperature of the calorimeter after the combustion reaction (assuming no heat is lost to the surroundings)? What is the ΔH_f of TNT?

Answers

1. C_p = C_s × (molar mass)

3. For Cu: q = 58 J; For Al: q = 130 J; Even though the values of the molar heat capacities are very similar for the two metals, the specific heat of Cu is only about half as large as that of Al, due to the greater molar mass of Cu versus Al: C_s = 0.385 and 0.897 J/(g•K) for Cu and Al, respectively. Thus loss of one joule of heat will cause almost twice as large a decrease in temperature of Cu versus Al.

5. 4.7 kJ

7. ΔH_soln = −0.56 kJ/g; based on reaction with AgNO₃, salt contains halide; dividing ΔH_soln values in Table 5.2 by molar mass of salts gives lithium bromide as best match, with −0.56 kJ/g.

9. T_final = 43.1°C; the combustion reaction is \[4C_7H_5N_3O_{6(s)} + 21O_{2(g)} \rightarrow 28CO_{2(g)} + 10H_2O_{(g)} + 6N_{2(g)}\] with \[Δ_f^οH (TNT) = −65.5\; kJ/mol\]

5.6: Hess's Law

---

Conceptual Problems

Please be sure you are familiar with the topics discussed in Essential Skills 4 (Section 5.6 "Essential Skills 4") before proceeding to the Conceptual Problems.​

1. Based on the following energy diagram,

   a. write an equation showing how the value of ΔH₂ could be determined if the values of ΔH₁ and ΔH₃ are known.

   b; identify each step as being exothermic or endothermic.

   

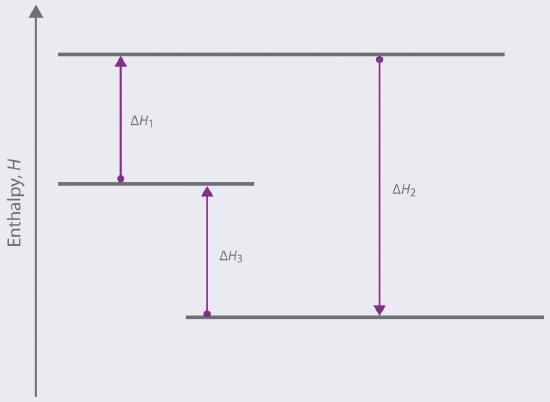
2. Based on the following energy diagram,

   a. write an equation showing how the value of ΔH₃ could be determined if the values of ΔH₁ and ΔH₂ are known.

   b. identify each step as being exothermic or endothermic.

   

3. Describe how Hess’s law can be used to calculate the enthalpy change of a reaction that cannot be observed directly.

4. When you apply Hess’s law, what enthalpy values do you need to account for each change in physical state?

   1. the melting of a solid
   2. the conversion of a gas to a liquid
   3. the solidification of a liquid
   4. the dissolution of a solid into water

5. In their elemental form, A₂ and B₂ exist as diatomic molecules. Given the following reactions, each with an associated ΔH°, describe how you would calculate ΔH^o_f for the compound AB₂.

   \( \begin{matrix}
   2AB & \rightarrow & A_{2} + B _{2} & \Delta H_{1}^{o}\\
   3AB & \rightarrow & AB_{2} + A _{2}B & \Delta H_{2}^{o} \\
   2A_{2}B &\rightarrow & 2A_{2} + B _{2} & \Delta H_{3}^{o}
   \end{matrix} \)

Numerical Problems

Please be sure you are familiar with the topics discussed in Essential Skills 4 before proceeding to the Numerical Problems.​

1. Methanol is used as a fuel in Indianapolis 500 race cars. Use the following table to determine whether methanol or 2,2,4-trimethylpentane (isooctane) releases more energy per liter during combustion.

   Fuel	ΔH^ocombustion(kJ/mol)	Density (g/mL)
   methanol	−726.1	0.791
   2,2,4-trimethylpentane	−5461.4	0.692

2. a. Use the enthalpies of combustion given in the following table to determine which organic compound releases the greatest amount of energy per gram during combustion.

   Fuel	ΔH^ocombustion(kJ/mol)
   methanol	−726.1
   1-ethyl-2-methylbenzene	−5210.2
   n-octane	−5470.5

   b. Calculate the standard enthalpy of formation of 1-ethyl-2-methylbenzene.

3. Given the enthalpies of combustion, which organic compound is the best fuel per gram?

   Fuel	ΔH^of(kJ/mol)
   ethanol	−1366.8
   benzene	−3267.6
   cyclooctane	−5434.7

Numerical Answers​

1.

2.

a. To one decimal place

methanol: ΔH/g = −22.6 kJ

​ C₉H₁₂: ΔH/g = −43.3 kJ

octane: ΔH/g = −47.9 kJ

Octane provides the largest amount of heat per gram upon combustion.

b, ΔH_f(C₉H₁₇) = −46.1 kJ/mol

5.7: Enthalpies of Formation

---

Conceptual Problems

Please be sure you are familiar with the topics discussed in Essential Skills 4 (Section 5.6 "Essential Skills 4") before proceeding to the Conceptual Problems.​​

1. Describe how Hess’s law can be used to calculate the enthalpy change of a reaction that cannot be observed directly.
2. When you apply Hess’s law, what enthalpy values do you need to account for each change in physical state?
3. What is the difference between ΔH^o_f and ΔH_f?
4. How can ΔH^o_f of a compound be determined if the compound cannot be prepared by the reactions used to define its standard enthalpy of formation?
5. For the formation of each compound, write a balanced chemical equation corresponding to the standard enthalpy of formation of each compound.
   1. HBr
   2. CH₃OH
   3. NaHCO₃
6. Describe the distinction between ΔH_soln and ΔH_f.
7. The following table lists ΔH^o_soln values for some ionic compounds. If 1 mol of each solute is dissolved in 500 mL of water, rank the resulting solutions from warmest to coldest.

Compound	ΔH^osoln(kJ/mol)
KOH	−57.61
LiNO3	−2.51
KMnO4	43.56
NaC2H3O2	−17.32

Numerical Problems

Please be sure you are familiar with the topics discussed in Essential Skills 4 (Section 5.6 "Essential Skills 4") before proceeding to the Numerical Problems.

1. Using "Appendix A, calculate ΔH^o_rxn for each chemical reaction.

   a. 2Mg(s) + O₂(g) → 2MgO(s)

   b. CaCO₃(s, calcite) → CaO(s) + CO₂(g)

   c. AgNO₃(s) + NaCl(s) → AgCl(s) + NaNO₃(s)

2. Using "Appendix A, determine ΔH^o_rxn for each chemical reaction.

   a. 2Na(s) + Pb(NO₃)₂(s) → 2NaNO₃(s) + Pb(s)

   b. Na₂CO₃(s) + H₂SO₄(l) → Na₂SO₄(s) + CO₂(g) + H₂O(l)

   c. 2KClO₃(s) → 2KCl(s) + 3O₂(g)

3. Calculate ΔH^o_rxn for each chemical equation. If necessary, balance the chemical equations.

   a. Fe(s) + CuCl₂(s) → FeCl₂(s) + Cu(s)

   b. (NH₄)₂SO₄(s) + Ca(OH)₂(s) → CaSO₄(s) + NH₃(g) + H₂O(l)

   c. Pb(s) + PbO₂(s) + H₂SO₄(l) → PbSO₄(s) + H₂O(l)

4. Calculate ΔH^o_rxn for each reaction. If necessary, balance the chemical equations.

   a. 4HBr(g) + O₂(g) → 2H₂O(l) + 2Br₂(l)

   b. 2KBr(s) + H₂SO₄(l) → K₂SO₄(s) + 2HBr(g)

   c. 4Zn(s) + 9HNO₃(l) → 4Zn(NO₃)₂(s) + NH₃(g) + 3H₂O(l)

5. Use the data in "Appendix A to calculate ΔH^o_f for the reaction Sn(s, white) + 4HNO₃(l) → SnO₂(s) + 4NO₂(g) + 2H₂O(l).

6. Use the data in "Appendix A to calculate ΔH^o_f for the reaction P₄O₁₀(s) + 6H₂O(l) → 4H₃PO₄(l).

7. How much heat is released or required in the reaction of 0.50 mol of HBr(g) with 1.0 mol of chlorine gas to produce bromine gas?

8. How much energy is released or consumed if 10.0 g of N₂O₅ is completely decomposed to produce gaseous nitrogen dioxide and oxygen?

9. In the mid-1700s, a method was devised for preparing chlorine gas from the following reaction:

   NaCl(s) + H₂SO₄(l) + MnO₂(s) → Na₂SO₄(s) + MnCl₂(s) + H₂O(l) + Cl₂(g)

   Calculate ΔH^o_rxn for this reaction. Is the reaction exothermic or endothermic?

10. Would you expect heat to be evolved during each reaction?

    1. solid sodium oxide with gaseous sulfur dioxide to give solid sodium sulfite
    2. solid aluminum chloride reacting with water to give solid aluminum oxide and hydrogen chloride gas

11. How much heat is released in preparing an aqueous solution containing 6.3 g of calcium chloride, an aqueous solution containing 2.9 g of potassium carbonate, and then when the two solutions are mixed together to produce potassium chloride and calcium carbonate.

Numerical Answers

1. a. −1203 kJ/mol O₂

   b. 179.2 kJ

   c. −59.3 kJ

5. −174.1 kJ/mol

7. −20.3 kJ

9. −34.3 kJ/mol Cl₂; exothermic

11. ΔH = −2.86 kJ CaCl₂: −4.6 kJ; K₂CO₃, −0.65 kJ; mixing, −0.28 kJ

5.8: Foods and Fuels

---

Conceptual Problems

1. Can water be considered a food? Explain your answer.
2. Describe how you would determine the caloric content of a bag of popcorn using a calorimeter.
3. Why do some people initially feel cold after eating a meal and then begin to feel warm?
4. In humans, one of the biochemical products of the combustion/digestion of amino acids is urea. What effect does this have on the energy available from these reactions? Speculate why conversion to urea is preferable to the generation of N₂.

Numerical Problems

Please be sure you are familiar with the topics discussed in Essential Skills 4 (Section 9.9 ) before proceeding to the Numerical Problems.

1. Determine the amount of energy available from the biological oxidation of 1.50 g of leucine (an amino acid, ΔH_comb = −3581.7 kJ/mol).

2. Calculate the energy released (in kilojoules) from the metabolism of 1.5 oz of vodka that is 62% water and 38% ethanol by volume, assuming that the total volume is equal to the sum of the volume of the two components. The density of ethanol is 0.824 g/mL. What is this enthalpy change in nutritional Calories?

3. While exercising, a person lifts an 80 lb barbell 7 ft off the ground. Assuming that the transformation of chemical energy to mechanical energy is only 35% efficient, how many Calories would the person use to accomplish this task? From Figure 9.4.2, how many grams of glucose would be needed to provide the energy to accomplish this task?

4. A 30 g sample of potato chips is placed in a bomb calorimeter with a heat capacity of 1.80 kJ/°C, and the bomb calorimeter is immersed in 1.5 L of water. Calculate the energy contained in the food per gram if, after combustion of the chips, the temperature of the calorimeter increases to 58.6°C from an initial temperature of 22.1°C.