1.2: Cycloaddition Reactions
- Last updated
- Save as PDF
- Page ID
- 450957
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objectives
After completing this section, you should be able to
- Identify cycloaddition reactions including the Diels-Alder reaction, dipolar cycloaddition, photo [2+2] reaction, thermal ketene [2+2] reaction, and ene reaction.
- Understand the orbital analysis of cycloaddition reactions
- Draw curved arrows to illustrate electron flow for cycloaddition reactions
- Given cycloaddition starting materials, accurately predict the product including stereochemistry
- Use retrosynthetic analysis to determine starting materials given a cycloaddition target
Key Terms
Make certain that you can define, and use in context, the key terms below.
- Diels-Alder reaction
- Diene
- Dienophile
- HOMO
- LUMO
- Dipolar cycloaddition
- Dipole
- Dipolarophile
- Photo [2+2] cycloaddition
- Ketene thermal [2+2] cycloaddition
- Ketene
- Ketenophile
- Ene reaction
- Ene
- Enophile
Study Notes
Cycloadditions are highly synthetically useful reactions that provide access to 4-, 5-, and 6-membered rings with excellent stereocontrol. Your goal is to understand the theoretical basis of these reactions using a molecular orbital analysis and to apply these reactions in synthesis. You should focus on accurately predicting products with a focus on stereochemistry and, given a complicated cyclic product, to accurately predict the starting materials used to generate it.
The previous section provided an overview of cycloaddition reactions. They are one class of pericyclic reactions that involve combination of two different pi systems to yield a cyclic product. They can be inter- or intramolecular and can produce all carbon and heterocyclic ring systems. They are powerful tools that synthetic chemists often employ to generate ring structures central to complex natural products. The following scheme highlights the four major types of cycloaddition reactions that we will study in this chapter: Diels-Alder reaction, dipolar cycloaddition, photo [2+2] reaction, and thermal ketene [2+2] reaction. We will also see an additional cycloaddition reaction, the ene reaction, that is related to the Diels-Alder reaction but doesn't form a ring.
Diels-Alder Reaction
The Diels-Alder reaction is a [4+2] cycloaddition (4 pi electrons from one reactant and 2 pi electrons from the other reactant) that yields a functionalized 6-membered ring product. It is the most useful cycloaddition reaction due to the ubiquity of 6-membered rings and its ability to reliably control stereochemistry in the product. Students generally learn about this reaction in introductory organic chemistry, so this section will start with an overview of key points before addressing more advanced concepts.
Regiochemistry
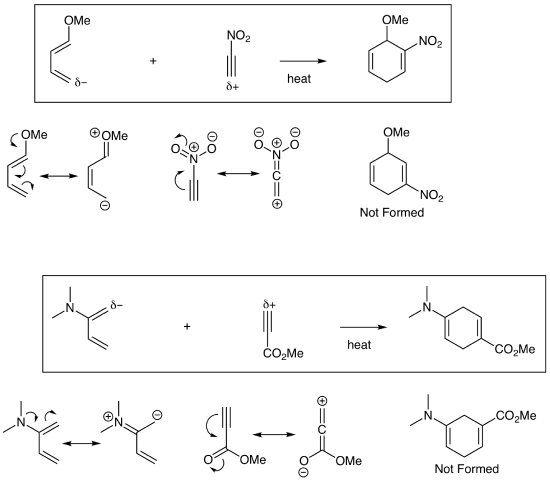
In standard Diels-Alder reactions, an electron rich diene (4 pi component) reacts with an electron poor dienophile (2 pi component). To determine how they combine, you must identify the most electron rich terminal atom of the diene and have that atom form a bond with the most electron poor atom of the dienophile. This is sometimes called the Ortho/Para Rule which can lead to confusion since we generally aren't making benzene products. We will avoid this memorization tool and instead focus on drawing resonance structures to find the key electron rich and electron poor atoms as demonstrated below. The examples below also demonstrate that the dieophile can be an alkyne which yields a cyclohexadiene product.
Stereochemistry - Stereospecific for Diene and Dienophile Atoms
Due to the concerted mechanism for cycloaddition reactions, the geometry of atoms on the dienophile or the diene maintain their orientation in the product. This is a critical point for the 4 atoms (both dienophile atoms and the terminal atoms of the diene) that become sp3 hybridized and thus are potential stereocenters in the product. (As a reminder, when chiral products are formed, we obtain a racemic mixture of enantiomers.) As highlighted below, cis dienophiles yield cis substituents in the product, while trans dienophiles yield trans product substituents. Substituents on the terminal atoms of the diene also can become stereocenters and this analysis is a little less straightforward than for dienophile substituents. The way to think about the diene substituents is whether the are pointing "outside" or "inside" the diene. These orientations are illustrated below. When groups are both pointing "outside" or "inside", we can consider them to be cis and they will end up cis in the product. When one group is pointing "outside" and one "inside", we can consider them as trans and they will be trans in the product. Note: CHO is a common abbreviation for an aldehyde.
Stereochemistry - Alder Endo Rule
The Alder Endo Rule enables us to predict the product stereochemistry when new stereocenters are created on atoms that originated in both the diene and dienophile. This rule is often described using the terms endo and exo in relation to the structure of bicyclic products. This is often confusing and difficult to apply in many circumstances. Instead we will define it in relation to substituents on the diene and dienophile. (We will explain the orbital origin of this rule shortly.) The Alder Endo Rule states the the electron withdrawing group on the dienophile (W group) ends up cis to groups pointing "outside" the diene in the cyclohexene product. The two reactions below illustrate the Alder Endo Rule and how to apply it. The second reaction highlights what we will see often in this section; cyclic dienes react with cyclic dienophiles to create complicated polycyclic products. We need to pay careful attention to stereochemistry in these cases and can use either option for drawing the result.
Transition State
Like all cycloaddition reactions, the Diels-Alder is concerted. Its mechanism has one transition state and no intermediates. The orientation of the reactants in the transition state determines the structure of the product. As previously mentioned, the way we can understand the mechanism is to look at the molecular orbitals involved. This will illustrate that there are primary orbital interactions (shown below in magenta), the orbitals that overlap to form new sigma bonds, and secondary orbital interactions (shown in blue), the orbitals that interact to give rise to the Endo Rule. The reactive conformation and transition state shown below illustrate that the stereochemistry is set when the reactants come together in the transition state with the W group pointing the opposite direction of the CH2 in the cyclopentadiene ring. Thus, the bridge in the bicyclic product (the CH2 from the reactant) is trans to the ketone.
Diels-Alder Drawing Tool
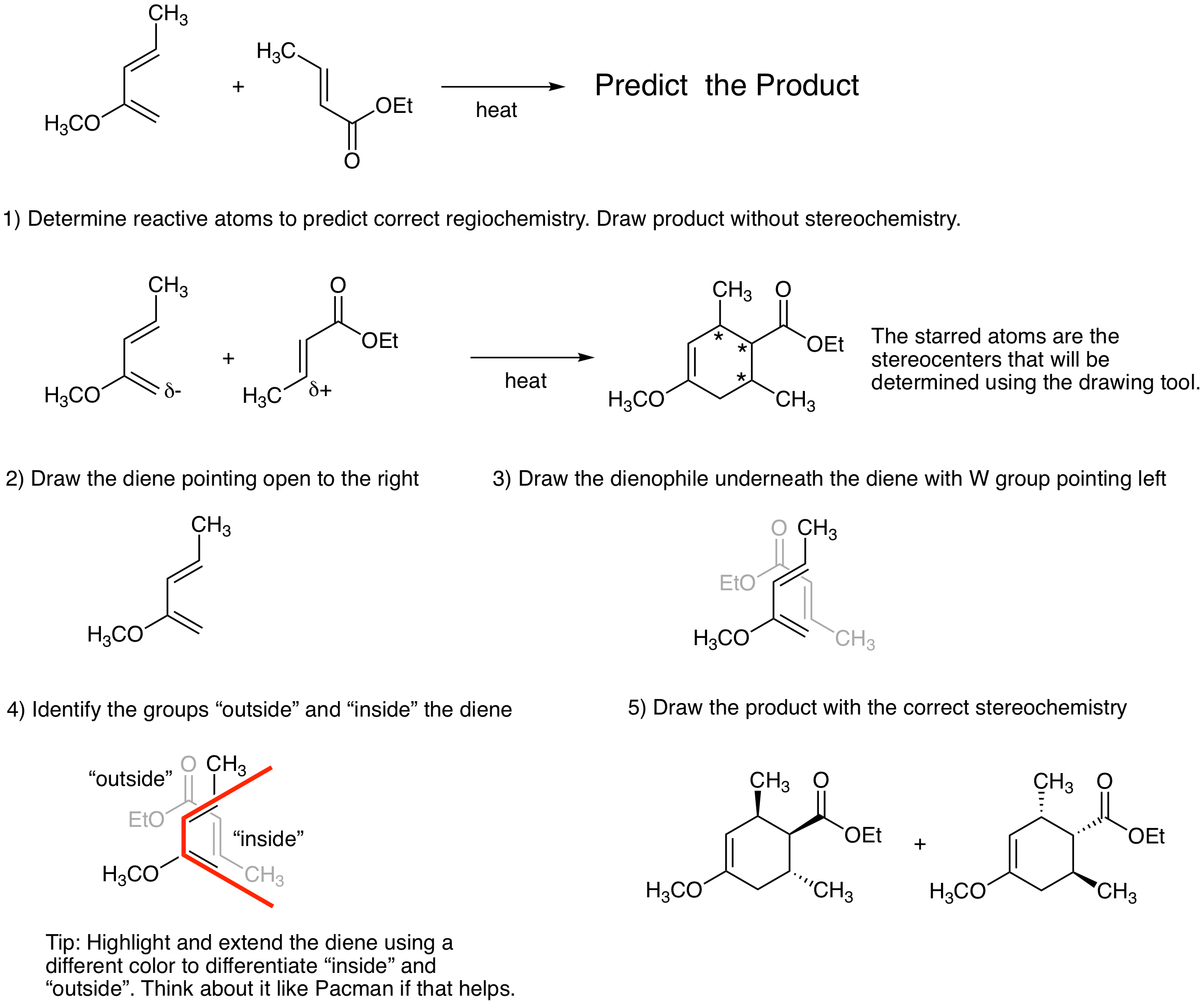
One way to keep track of stereochemistry in the Diels-Alder reaction is to use a drawing tool that mimics the reactive conformation. Note: Follow the rule for determining the regiochemistry and be sure to place the most electron rich terminal atom of the diene next to the most electron poor atom of the dienophile when using this tool. It is easy to get the incorrect product if you forget this step. First, draw the structure of the cyclohexene product ignoring stereochemistry. (The next steps will enable you to determine the stereoechemistry in the product.) Second, draw the diene with the opening pointing to the right. Third, draw the dienophile underneath the diene with the W group pointing left. Fourth, identify substituents that are positioned "outside" the diene and substituents that are positioned "inside" the diene. All groups "outside" will be cis in the product. All groups "inside" will be cis in the product. "Outside" groups will be trans to "inside" groups in the product. The figure below illustrates how to use the drawing tool. Fifth, redraw the product with all of stereochemistry.
Exercise \(\PageIndex{1}\)
Predict the product of this intermolecular Diels-Alder reaction. Clearly show both enantiomers of the product.
- Answer
-
Exercise \(\PageIndex{2}\)
Predict the product of this intramolecular Diels-Alder reaction. Clearly show both enantiomers of the product.
Hints: For intramolecular reactions, regiochemistry considerations are often ignored because one bicyclic structure is much more stable than the other possibility. Be sure to number out the starting material to identify the cyclohexene that will form and the size of the other ring that is produced as a result of the Diels-Alder reaction. Try your best to redraw the molecule in a reactive conformation. The Drawing Tool also works well for intramolecular reactions to help determine the stereochemistry of the product.
- Answer
-
Exercise \(\PageIndex{3}\)
Propose a synthesis of the following substituted cyclohexane.
Hints: This takes more than one step. Try to think retrosynthetically. Focus on forming the stereocenters using the Diels-Alder reaction. Think about the electronic requirements of the Diels-Alder reaction.
- Answer
-
This target is a substituted cyclohexane. The Diels-Alder reaction yields a substituted cyclohexene. So, this product was likely made by alkene hydrogenation of a Diels-Alder product. When thinking backwards, this means we need to determine which position in the six-membered ring contained the double bond. We know that the Diels-Alder reaction is an excellent method for making stereocenters, so we should assume the carbons with the aldehyde and isopropyl groups aren't part of the alkene. We also know that standard Diels-Alder reactions have electron withdrawing groups on the dienophile, so we should place the alkene in a position where the aldehyde starts on the dienophile. This leads to two possibilities for cyclohexene targets.
In option A, the atoms that will become stereocenters originate on both the diene and dienophile. This means that the isopropyl group must point "inside" the diene to yield the trans product according to the Endo Rule. This type of diene conformation is sterically very hindered as can be seen just looking at the image, so the diene will prefer to be in an unreactive conformation (rotate the singe bond between the two alkenes) and this reaction will occur slowly. Option B has no drawbacks. We have a simple and reactive diene and a trans dienophile that will yield the desired trans product.
The synthesis follows in two steps from the retrosynthetic analysis.
Forming Heterocycles with the Diels-Alder Reaction
There are many fascinating applications of the Diels-Alder reaction. We have already seen in the problems above that we will encounter intramolecular Diels-Alder reactions to enable us to make complicated polycyclic targets. We will also encounter hetero Diels-Alder reactions where one or more atoms of the diene or dienophile contains atoms other than carbon. Oxygen and nitrogen are most popular and will enable us to make six-membered heterocyclic rings, as shown below. Additionally, it is important to note that Diels-Alder reactions can be promoted not only with heat but also with Lewis acids. These reagents bind to the dienophile electron withdrawing group, making the most reactive carbon more electron poor and, thus, more reactive.
With the right combination of diene, dienophile, and an interesting cascade mechanism, the Diels-Alder reaction can yield benzene products. The reaction shown below is one example. This is a two step process involving a cycloaddition and a cycloreversion. Try to generate a mechanism to explain this interesting reaction. Why is this a favorable process?
Exercise \(\PageIndex{4}\)
Propose a mechanism and explain why this is a favorable reaction.
- Answer
-
The first step is the Diels-Alder reaction that we would expect to yield the bicyclic intermediate that then breaks down via a retro Diels-Alder reaction (cycloreversion). The intermediate isn't the product because the cycloreversion yields a stable aromatic product and generates a stable gaseous product that bubbles out of the reaction.
Diels-Alder Reaction and Retrosynthetic Analysis
In one of the problems above, we introduced the idea of thinking backwards using retrosynthetic analysis to help us determine the diene and dienophile that could react to yield a target six-membered ring. This is a skill that we will use often when analyzing complicated targets. The key structural fragment, or retron, that we look for in a molecule that alerts us that we can make it by a Diels-Alder reaction is a six-membered ring. More specifically, it's a six-membered ring containing one pi bond. For a traditional all-carbon Diels-Alder reaction, the retron is a cyclohexene. The following examples highlight how we can use retrosynthetic analysis for standard synthesis problems.
Exercise \(\PageIndex{5}\)
Propose a Diels-Alder reaction that will yield each of the target molecules.
- Answer
-
Begin your retrosynthetic analysis by performing a retro Diels-Alder reaction to reveal the diene and dienophile that can combine to make your target. Draw your first curved arrow by starting at the alkene in the six-membered ring. Move the electrons clockwise or counterclockwise then draw the resulting diene and dienophile. The stereochemistry in the product will dictate how the subsitutuents are arranged on the starting materials. In this case, the dienophile contains a nitro electron withdrawing group and a trans methyl. The methoxy substituent on the diene must be pointing out since it ends up cis to the nitro group in the product. The methyl group on the diene must be pointing in because it is trans to the methoxy in the product.
It is often helpful to number all of the atoms in the product before beginning your retrosynthetic analysis. For complicated structures, like this bicyclic target, it is essential to number the atoms. We use the same strategy as the first problem by beginning our curved arrows for the retro Diels-Alder at the alkene. This reveals that we are breaking C1-C10 and C4-C9 and that we must perform an intramolecular Diels-Alder to generate the target. Be sure to pay attention to stereochemistry which reveals that the dienophile stereochemistry is trans (since C8 and C11 are trans in the product). Since C5 and the ketone withdrawing group are cis, C5 must be pointing out on the diene.
Synthetically Useful Diels-Alder Dienes
There are several other specific target structures that we need to become familiar with since they will show up in future synthetic applications. The first is a bicyclic 6,6 system with one benzene ring. This is a retron for a Diels-Alder reaction using an ortho-quinodimethane diene. Dienes of this type are highly reactive and are generally made by two different strategies. One is an electrocyclic ring opening, a reaction we will study in more detail in the next chapter, and the other is a fluoride promoted vinylogous elimination reaction.
Conjugated cyclohexenones are highly valuable synthetic building blocks. These types of structures are often made using enolate chemistry, specifically the Robinson annulation. They can also be synthesized via the Diels-Alder reaction using a diene developed by Sam Danishefsky which is known as Danishefsky's diene. The Diels-Alder retron for use of this diene is shown below along with the complete retrosynthetic analysis and the structure of Danishefsky's diene. The Diels-Alder product of this reaction yields the target cyclohexenone upon treatment with acid. Propose a mechanism for this process which is a good review of acid promoted carbonyl-type chemistry.
Exercise \(\PageIndex{6}\)
Propose a mechanism for the conversion of the Diels-Alder product from use of Danishefsky's diene into the target cyclohexenone product upon treatment with acid.
- Answer
-
Diels-Alder Reaction Orbital Analysis
To understand why the Diels-Alder reaction occurs thermally and not photochemically, we must analyze the molecular orbitals involved in the reaction. This type of analysis, often called the Woodward-Hoffmann Rules, was introduced in the previous chapter. We will take a deeper look in this section. As mentioned previously, cycloadditions combine two independent pi systems to form two new sigma bonds. We must have constructive overlap between the Highest Occupied Molecular Orbital (HOMO) of one system (the nucleophile) and the Lowest Unoccupied Molecular Orbital (LUMO) of the other system (the electrophile). There are two possible modes or overlap: suprafacial, where both sigma bonds form on the same side of the pi system, and antarafacial, where the sigma bonds form on opposite sides of the pi system. Examples similar to these modes of overlap are also found in alkene reactions. Suprafacial reactions are similar to alkene syn additions (e.g., H2, cat. Pd/C) while antarafacial reactions are similar to alkene anti additions (e.g., Br2). The Diels-Alder reaction is suprafacial with respect to both diene and dienophile, as illustrated below. (The diene is on the top; the dienophile on the bottom. Dashed black lines are nodes; dashed magenta lines are constructive overlap where new sigma bonds can form.) Two examples of antarafacial reactions (that don't actually occur) are shown for comparison. Antarafacial cycloadditions are very unusual, and we will only discuss one example, the ketene thermal [2+2] reaction that will be introduced later in this chapter.
The molecular orbital analysis for cycloadditions involves several steps. First, determine how many atoms from each component are involved in the reaction and draw out their pi molecular orbitals. For the Diels-Alder reaction, there are 4 atoms with p orbitals in the diene and 2 atoms with p orbitals in the dienophile. The reactive orbitals for the Diels-Alder reaction are pi molecular orbitals, so we will focus on the pi MOs for both the diene and dienophile. The dienophile has one pi bond, so we will look at the pi MOs for a 2 atom system. The diene has two pi bonds, so we will look at the pi MOs for a 4 atom system. The details are shown below. We will use these MO Diagrams for all types of pericyclic reactions, they are not specific to the Diels-Alder reaction or cycloadditions.
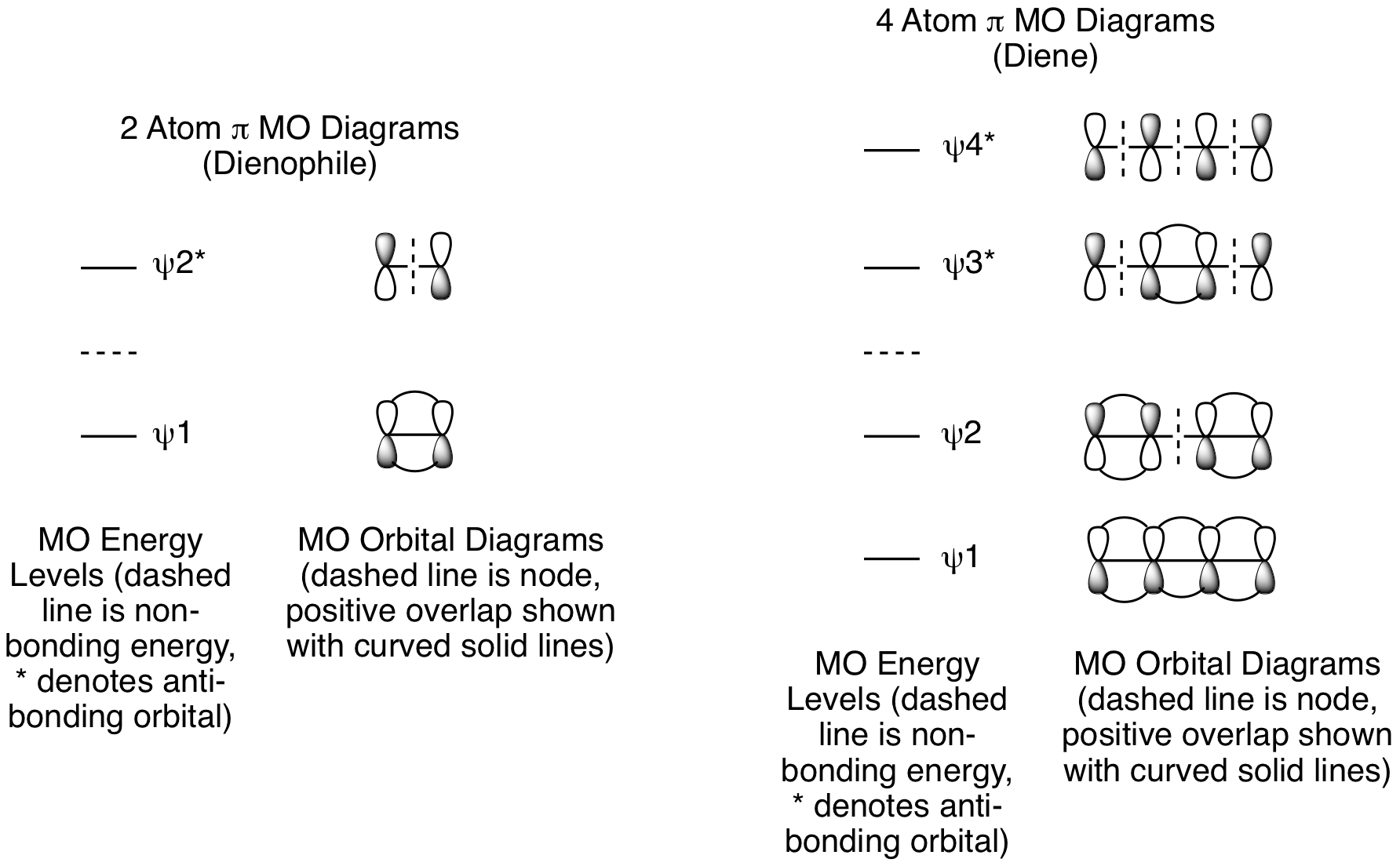
Second, add electrons to the pi MOs to determine the HOMO and LUMO for each reactant. The dienophile has 1 pi bond, so it has 2 pi electrons. The diene has 2 pi bonds, so it has 4 pi electrons. For the dienophile, the HOMO is psi 1 and the LUMO is psi 2*. For the diene, the HOMO is psi 2 and the LUMO is psi 3*.

Third, determine if the reaction is possible by combining the HOMO of one component with the LUMO of the other. In a standard Diels-Alder reaction, an electron rich diene reacts with an electron poor dienophile. This means the diene is the nucleophile and reacts from the HOMO, while the dienophile is the electrophile and reacts from the LUMO. The opposite electronic arrangement, diene LUMO plus dienophile HOMO, is also possible. This is known as an Inverse Electron Demand Diels-Alder reaction. Both possibilities are illustrated below. These diagrams clearly demonstrate these reactions are suprafacial with respect to both the diene and dienophile, and, thus, they will happen. (Note: As always, dashed black lines are nodes and dashed magenta lines are positive orbital overlap that results in new sigma bond formation. Solid curved lines showing positive orbital overlap have been omitted for clarity.) To avoid potential confusion, we will delay analysis of photochemical cycloadditions until a little later in the chapter when we get to photo [2+2] reactions. If we did analyze the Diels-Alder under photochemical conditions, it would confirm that this is not possible.
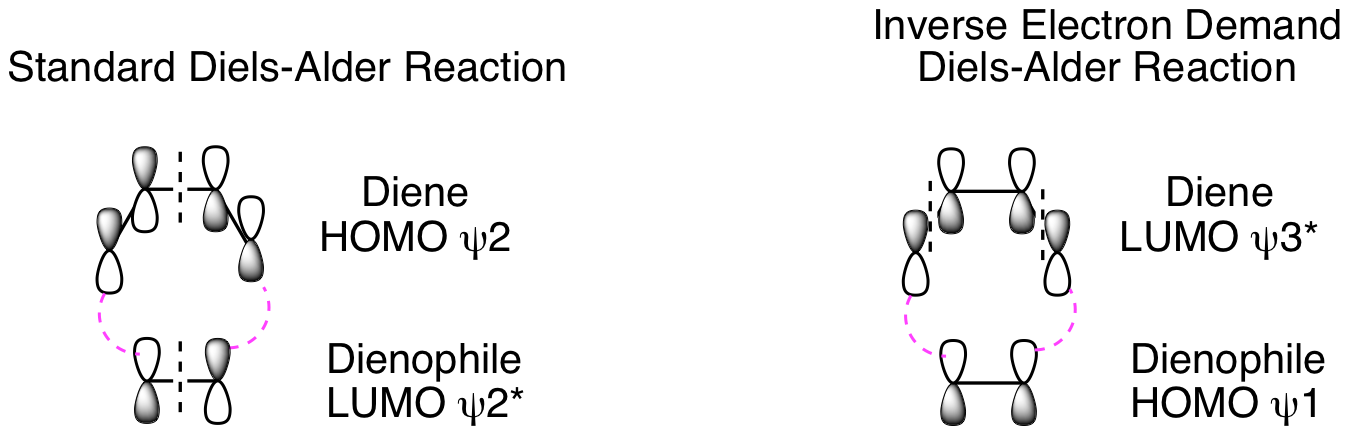
Dipolar Cycloaddition Reactions
Another useful thermal reaction is the dipolar cycloaddition which provides ready access to a variety of 5-membered ring heterocycles. The retron for a dipolar cycloaddition is a five-membered ring heterocycle. The key reaction component is a 3-atom dipole generally consisting of a pi bond adjacent to a negatively charged atom with a lone pair. This provides 4 electrons for the reaction, 2 electrons in the pi bond and 2 electrons from the delocalized lone pair. Thus, this reaction is electronically equivalent to the Diels-Alder reaction with the dipole contributing 4 pi electrons and the dipolarophile contributing 2 pi electrons. Two common 3 atom dipoles that many students encounter in previous organic chemistry classes are diazomethane and ozone. In fact, the ozonolysis mechanism, pictured below, is a wonderful example of dipolar cycloadditions in action. The first step is a dipolar cycloaddition which is followed by a retro dipolar cycloaddition (a cycloreversion). (Note: Retro dipolar cycloadditions are very unusual.) After a molecular rotation of one or the other component, a second dipolar cycloaddition occurs to yield an intermediate that is stable until the reaction is worked up under either oxidative or reductive conditions. This is a very complicated transformation. Problems that we will see using dipolar cycloadditions will generally be much more straightforward. As we will see in the problems that follow, the dipole and dipolarophile can contain triple bonds and, like all cycloadditions, this reaction can occur intramolecularly.
Exercise \(\PageIndex{7}\)
What product is generated in each of the following reactions?
- Answer
-
Part a) demonstrates the utility of a dipolar cycloaddition to make an aromatic heterocycle. Think about the regiochemistry of this one based on the electronic analysis we did for the Diels-Alder reaction. In this case, the dipole is the nucleophile with the negatively charged oxygen. Think about why the internal carbon on the alkyne is the most electron poor.
Part b) is complicated because of the challenging tricyclic structure that forms in the reaction. This is an example where numbering the atoms is critical and building a model is a huge help.
The orbital analysis of dipolar cycloadditions is very similar to the Diels-Alder reaction, though it requires us to understand how to generate the pi molecular orbital picture for a 3 atom system (illustrated below). If you have already studied pi molecular orbitals for an allyl system (radical, carbocation, or anion), the dipole in our reactions can be treated as an allyl anion. This is consistent with what we said previously about the dipole being a 3 atom system that has 4 pi electrons. In standard dipolar cycloadditions, the electron rich component is the dipole which reacts from the psi 2 HOMO while the electron poor dipolarophile reacts from the psi 2* LUMO. The orbital picture of the dipolarophile is identical to the Diels-Alder dienophile, both are two atom pi systems. Like the Diels-Alder reaction, the electronics can be reversed so that an electron poor dipole reacts with an electron rich dipolarophile, psi 3* LUMO plus psi 1 HOMO, respectively. Both options are shown below.

Photo [2+2] Cycloadditions
Photochemical [2+2] cycloadditions are excellent reactions for the synthesis of strained products containing 4-membered rings. They produce all carbon and heteroatom rings by both inter- and intramolecular reactions. One of the reaction partners must be conjugated so that it can absorb light and become an excited state molecule. These reactions produce strained 4-membered rings but are not reversible because the products lack conjugation and, thus, can't absorb light to facilitate a cycloreversion.
Stereochemistry in photo [2+2] reactions is more straightforward than the Diels-Alder reaction. The steochemistry present in each reactant is maintained in the product, so cis alkenes yield cis product substituents and vice versa. When comparing possible stereochemistry between the two reactants, the least hindered product is favored. For example, in the reaction below, the all cis product is not formed; the trans structure is generated.
Because this is a photochemical reaction, predicting regiochemistry is the opposite of what we would expect from our standard analysis of thermal reactions like in the Diels-Alder reaction. This result is illustrated below. Instead of combining the most electron rich atom in one reactant with the most electron poor atom of the other reactant, it looks like we are combining the most electron rich atom with the other most electron rich atom (or vice versa). Why does this happen? It is important to remember that, as we will see in more detail shortly, one of the reactants participates in the reaction in its excited state. Molecules in the excited state have the opposite electron configuration than in the ground state. So, the most electron rich atom becomes the most electron poor atom and vice versa. One way to accurately predict the correct regiochemistry is to determine the correct ground state regiochemistry then switch the substituents to get the correct photoreaction regiochemistry.
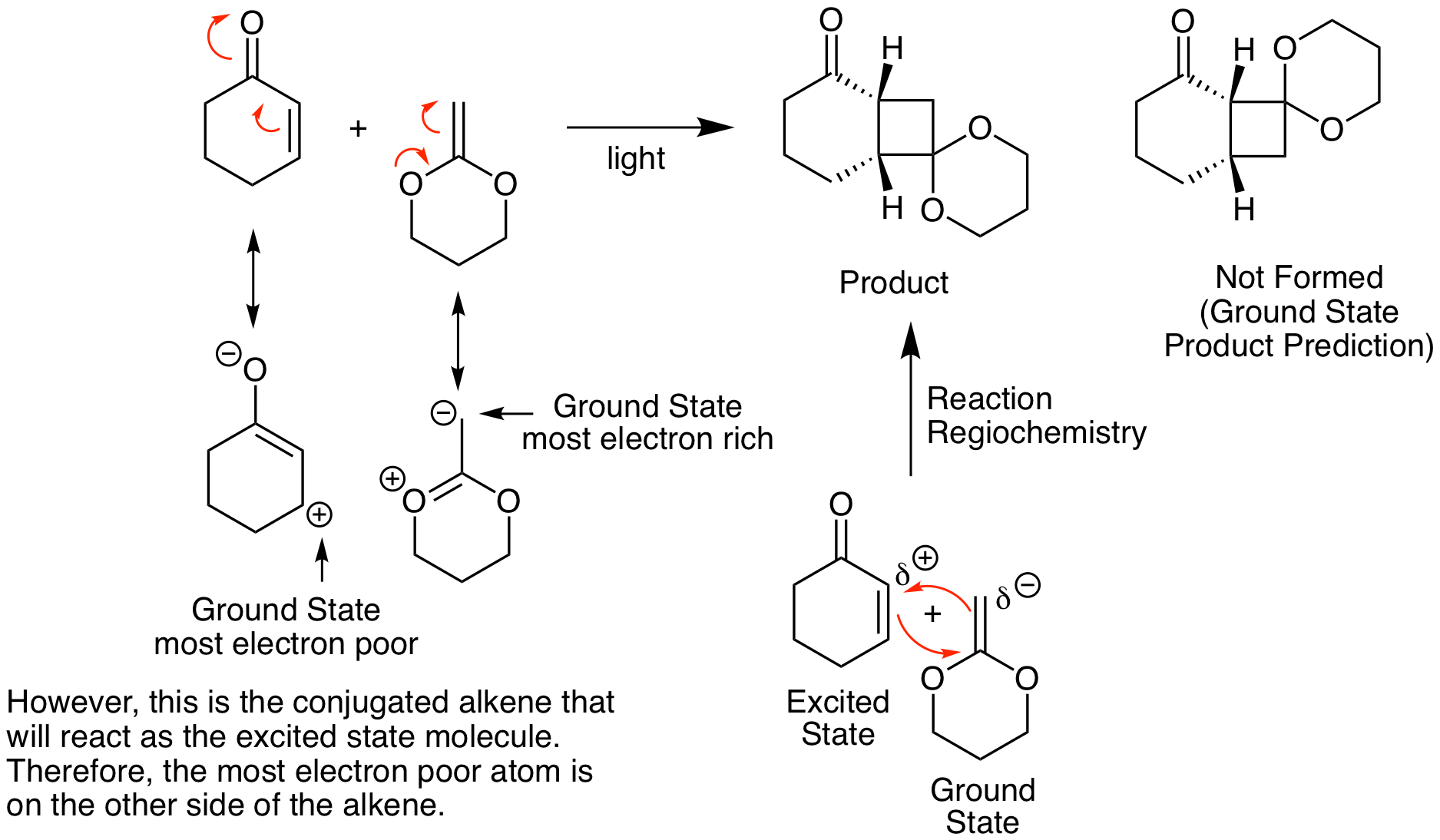
So, why won't this reaction happen thermally? How does our molecular orbital analysis help us understand the importance of this being a photochemical reaction? First, let's look at the orbital analysis if we tried to do a thermal [2+2] reaction. As shown below, we cannot get suprafacial overlap for both of the 2 pi reactants when trying to combine psi 1 HOMO with psi 2* LUMO. This means that it is not favorable to convert the two reactant pi bonds into two new product pi bonds.
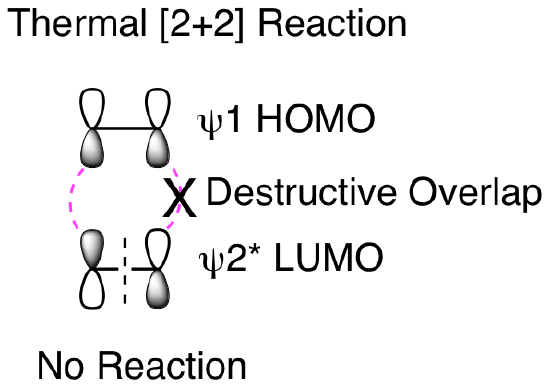
What happens when we shine light on the reaction? Light creates an excited state molecule by promoting an electron in the HOMO to the LUMO, as shown below. This means the excited state HOMO is the ground state LUMO. We need to understand a few key points about photoreactions before doing our molecular orbital analysis. Excited state molecules are very short lived, relaxing back to the ground state very quickly. Therefore, it is practically impossible for two excited state molecules to find each other in a reaction. Instead, reactions occur between one excited state molecule and one ground state molecule. When only one molecule is conjugated, that is the molecule that will form the excited state. If both reactants are conjugated, either can form the excited state. The orbital analysis is shown below. First, we see the orbital picture when a ground state molecule absorbs light to form an excited state. Second, when we analyze the reaction, it is now psi 2* HOMO of the excited state molecule reacting with psi 2* LUMO of the ground state molecule. This gives suprafacial constructive overlap for both orbitals and the 2 reactant pi bonds can be converted into two product sigma bonds. The reaction occurs!
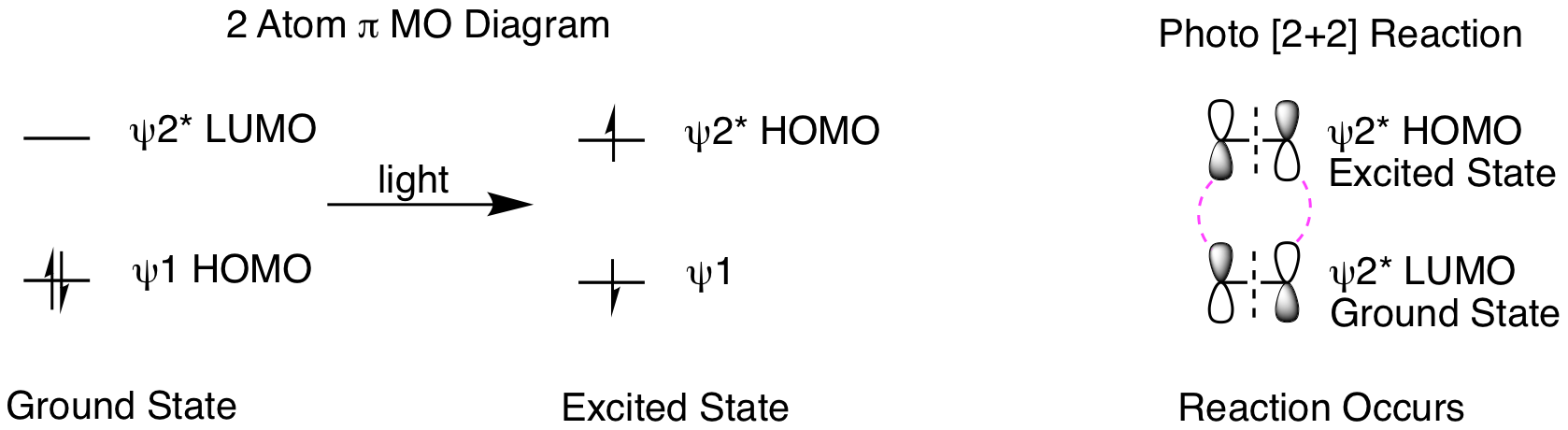
Exercise \(\PageIndex{8}\)
What are the products of the following two reactions? Hints: For a), this is an example of a hetero photo [2+2] cycloaddition. For b), your product is the result of two cycloadditions.
- Answer
-
Part a is known as a Paterno-Bucchi reaction. It's a photo [2+2] reaction that combines a carbonyl with an alkene to form an oxetane. Also, like many organic reactions, it is very unusual for benzenes to participate in cycloadditions. Don't forget to think about stereochemistry and regiochemistry when drawing your product. Since the two benzenes start on each of the reactants, they will end up trans in the product because this is sterically favored. Performing our ground state analysis, it becomes clear that the molecule in the box is the product from the photoreaction.
Part b combines a Diels-Alder reaction with a photo [2+2] to make a very interesting and highly strained product. Using photochemistry to generate strain in a target molecule is a very useful synthetic strategy.
Ketene Thermal [2+2] Cycloaddition
Ketenes are unusual functional groups that react in unexpected ways. (Ketenes contain an sp hybridized carbon connecting a carbonyl directly to an alkene. The all carbon equivalent is an allene. The 2 pi bonds in ketenes and allenes are not conjugated; they are perpendicular.) The most common ketene reaction is a thermal [2+2] cycloaddition. We will explore the orbital explanation for this shortly. First, let's look at a common method for the synthesis of ketenes and an example of a reaction. Ketenes can be reliably synthesized upon reaction of an acid chloride with a non-nucleophilic amine base, in this case triethylamine, via an elimination reaction. Once formed, the ketene undergoes a [2+2] cycloaddition to yield a cyclobutane product. This reaction follows the same stereochemistry rules as photo [2+2] cycloadditions. Since this is a thermal reaction, the regiochemistry is straightforward. Find the most electron rich atom in the ketenophile and react it with the highly electron poor carbonyl carbon of the ketene.

The orbital analysis is exactly the same as our discussion of the photo [2+2] reaction above except that the thermal reaction that doesn't occur in that analysis is now happening. How is that possible? The critical factors are that the ketene carbonyl carbon is both electron poor and unhindered since no other substituents are attached. This means that the ketenophile reacts in a suprafacial orientation from HOMO psi 1 while the ketene reacts in an antarafacial fashion from LUMO psi 2*, as depicted below. This antarafacial reactivity is only possible because of the sp hybridization and resulting lack of steric hinderance for the approaching ketenophile. Thinking about this in three dimensions helps visualize how this is possible (see representation below).
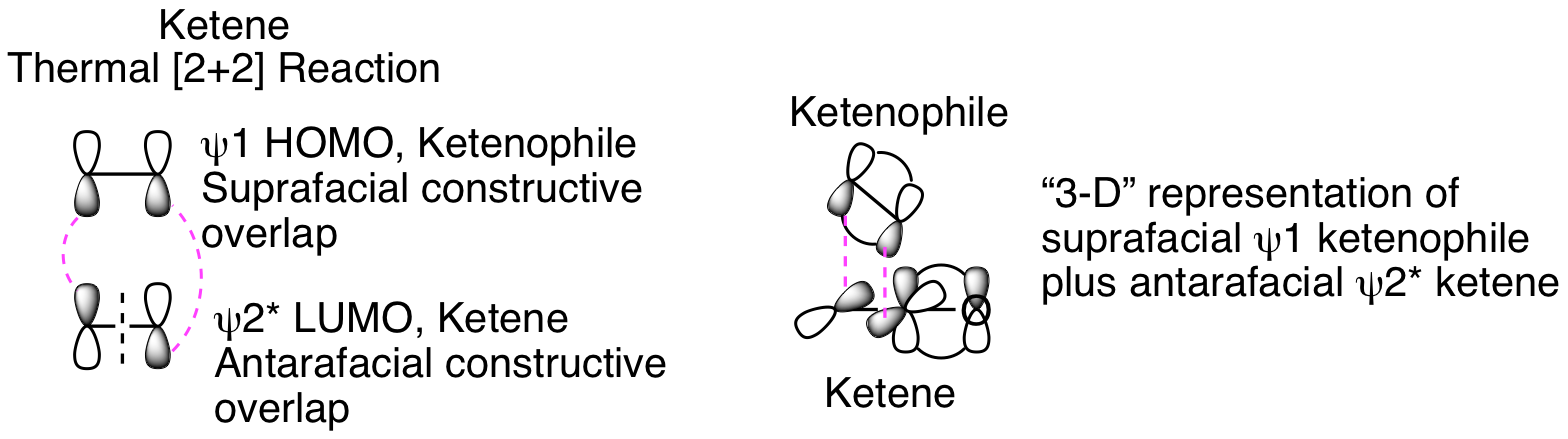
It is normally impossible to see the result of this suprafacial plus anatarafacial reactivity, but the following intramolecular ketene [2+2] reaction clearly illustrates the reaction mechanism. Instead of the standard fused bicycylic product that would result from a suprafacial plus suprafacial reaction, the more complicated bridged bicyclic product is generated. This is only possible because of the suprafacial plus antarafacial reactivity.
Exercise \(\PageIndex{9}\)
Predict the product of the following reaction.
- Answer
-

This problem demonstrates to power of the ketene thermal [2+2] reaction to make heterocycles. Combination of a ketene with an imine yields a 4-membered ring amide which is known as a beta lactam. This functional group is present in bioactive molecules like penicillin.
Ene Reaction
Our final cycloaddition reaction is another transformation discovered by Kurt Alder. The Diels-Alder reaction was originally know as the "diene reaction". This transformation involves an alkene, so it was named the "ene reaction". An example with the mechanism is shown below. The alkene is the 4 electron component reacting with its pi bond and an allylic C-H bond. The enophile is the 2 electron component making this another thermal [4+2] reaction. Intermolecular ene reactions happen only with very electrophilic alkenes or alkynes and often with a Lewis acid catalyst. Intramolecular reactions are much more common and occur with heating or Lewis acid catalysis.

So, is this really a cycloaddition reaction since we aren't using pi bonds in the mechanism? Yes, it is. As we will see in subsequent chapters, sigma bonds, especially C-H bonds, can participate in pericyclic reactions. The orbital picture is shown below where we treat the sigma plus pi bonds of the ene as a 4 atom system. Thus, the reaction occurs between HOMO psi 2 of the ene and LUMO psi 2* of the enophile. With 4 electrons from the ene and 2 electrons from the enophile, this is another 6 electron, thermally allowed cycloaddition, just like the Diels-Alder reaction and dipolar cycloaddition.

Exercise \(\PageIndex{10}\)
What products are formed in the following reactions? Hint: For b, the product contains a new 5-membered ring.
- Answer
-
The most common version of the ene reaction is known as the "carbonyl ene reaction" where the enophile is a carbonyl, usually an aldehyde. This generates a product that is a homoallylic alcohol which is the retron for a carbonyl ene reaction. An example is shown below.
An application of the carbonyl ene reaction is the two-step conversion of citronellal to menthol, as shown below. The first step is an intramolecular carbonyl ene reaction followed by an alkene hydrogenation. An interesting question is how is the stereochemistry controlled in the ene reaction? Like many reactions that we will see in subsequent chapters, the key is a chair-like 6-membered ring transition state. With the stereogenic methyl positioned equatorial, this enables the developing stereocenters, the OH and the propene, to be equatorial in the transition state. Try to remember this strategy when thinking about stereochemistry for intramolecular reactions in the future, not just the ene reaction.
Summary Problems
Exercise \(\PageIndex{1}\)
In 2012, Tom Hoye from the University of Minnesota reported a novel Diels-Alder reaction called the Hexadehydro-Diels-Alder reaction with a diyne as the diene and another alkyne as the dienophile. Hint: Benzyne plays a critical role in this reaction mechanism.
a) Here’s an example of this novel type of Diels-Alder reaction. Propose a mechanism for this transformation. Hint: The first step is an intramolecular Diels-Alder reaction.
b) Using the mechanism you determined in part a, determine the product of this reaction.
- Answer
-
DOI - 10.1038/nature11518 (Nature 2012)
a) The Diels-Alder reaction yields a cyclic allene that is one of the resonance structures for benzyne. So, this is a cycloaddition that yields a benzyne intermediate! Under these reaction conditions, the benzyne reacts as its polar resonance structure to first deprotonate acetic acid and then combine with acetate to yield the final product.
b) In this example, without the addition of acid, the benzyne intermediate deprotonates the sulfonamide proton. The resulting negatively charged nitrogen forms an intramolecular C-N bond resulting in the synthesis of a new 5-membered ring.
Exercise \(\PageIndex{2}\)
In 1964, Prof. Phil Eaton at the University of Chicago achieved the first synthesis of cubane. A key molecule in his synthesis is shown below. This compound can be prepared in two steps via dimerization (one molecule reacting with itself) of a monocyclic compound followed by an intramolecular reaction. Determine the structure of the starting material and the two reactions needed to prepare the key synthetic intermediate. Hint: Both reactions are cycloadditions. (Don’t worry about how to convert the dibromide into cubane.) As a bonus question, how many peaks do you predict will be in the 1H and 13C NMR spectra for cubane?
- Answer
-
DOI - 10.1021/ja01069a041 (Journal of the American Chemical Society 1964)
There are several possible photo [2+2] disconnections, but this one reveals a tricyclic compound that can be made by a Diels-Alder reaction between two of the same bromocyclopentadienone molecules. It is a remarkable two-step sequence to generate the highly complex key synthetic intermediate. For the question of cubane's NMR spectra, this molecule is fully symmetrical and yield only one peak in both the 1H and 13C NMR spectra.

