16.1: Trends in Kinetic Lability

CHEM 431: Inorganic Chemistry
Fall 2020: Dr. Kathryn Haas

 Home    ●   Readings   ●  Course Info & Tools 

---

Introduction

Kinetics is a branch of chemistry that is concerned with the rates of chemical reactions. In this section, we will discuss the rates of metal-ligand (M-L) substitution reactions.

Let's start with some examples. In the table below are three examples of ligand substitution reactions of hexaaquo metal complexes to form hexaammine complexes. These reactions are nearly identical with the exception of the metal ion. The products are thermodynamically favored in all cases.

Reaction	Rate constant (\(k\))	Labile or Inert
\([Ni(OH_2)]^{2+} + 6 NH_3 \rightleftharpoons [Ni(NH_3)_6]^{2+}\)	\(k = 10^{4} s^{-1}\) (1 ns)	Labile (happens in < 1 min)
\([Cr(OH_2)]^{3+} + 6 NH_3 \rightleftharpoons [Cr(NH_3)_6]^{3+}\)	\(k = 10^{-3} s^{-1}\) (6 days)	Inert (slow, takes hours)
\([Cu(OH_2)]^{2+} + 6 NH_3 \rightleftharpoons [Cu(NH_3)_6]^{2+}\)	\(k = 10^{8} s^{-1}\)	Very Labile (happens in seconds)

DefinitionS

• Labile - Metal complexes that undergo "kinetically fast" substitution reactions are labile. These reactions usually happen in less than one minute.
• Inert - Metal complexes that undergo "kinetically slow" substitution reactions are inert or non-labile. These reactions usually take hours.
• Intermediate - Metal complexes that undergo "kinetically intermediate" substitution reactions are intermediate.

A common pitfall is to confuse the meaning of kinetic terms, like labile and inert, with thermodynamic terms, like stable and unstable. It is important to distinguish between kinetics and thermodynamics. For example, the complex \([Fe(H_2O)Cl]^{2+}\) has a large formation constant and is thermodynamically stable; yet it is also labile. On the other hand, the complex \([Co(NH_3)_6]^{3+}\) is unstable in acidic aqueous solution and decomposes spontaneously to \([Co(H_2O)_6]^{3+}\); yet it decomposes slowly because it is inert. It is good practice to distinguish between meanings by using terms such as "kinetically labile" or "kinetically inert" and "thermodynamically stable" and "thermodynamically unstable".

Exercise \(\PageIndex{1}\)

Draw the reaction coordinate diagrams for a reaction of the form \([ML_6]^{n+} + X \rightleftharpoons [ML_5X]^{n+} + L\) in the following scenarios:

1. \([ML_6]^{n+}\) is theromdynamically stable and kinetically inert.
2. \([ML_6]^{n+}\) is theromdynamically unstable and kinetically inert.
3. \([ML_6]^{n+}\) is theromdynamically stable and kinetically labile.
4. \([ML_6]^{n+}\) is theromdynamically unstable and kinetically labile.

Answer a)

Answer b)

Answer c)

Answer d)

 

---

Factors that affect rates of substitution reactions:

Some of the factors that affect rates of ligand substitution reactions are those that also affect thermodynamic stability. It is important to remember that kinetic and thermodynamic factors are related, yet separate. The same factors that make a complex stable can also make it more inert. However, it is incorrect to assume that stability is always correlated with reaction rates.

Why are kinetic factors related to thermodynamic stability? For a complex to react or exchange one ligand for another, it must change its geometry to form an intermediate or transition state. For example, inert octahedral complexes often have stable electron configurations. When the reactant electron configuration is particularly stable, it can result in a higher activation energy associated with moving away from the stable configuration.

Factors to consider:

1. Electron configuration and LFSE: Electron configurations that place electrons in higher-energy orbitals (particularly antibonding orbitals) result in more labile complexes. As long as there are not electrons in higher-energy orbitals, the lability correlates roughly with LFSE. The more negative the LFSE, the more inert.
2. Size and charge of the metal ion: In general, higher charge denisity on the metal ion leads to stronger electrostatic attraction between metal and ligand; higher charge density generally correlates with slower rates of ligand substitution.

---

Taube's observations of metal complex substitution rates

Henry Taube (Nobel Prize, 1983) tried to understand lability by comparing the factors that govern bond strengths in ionic complexes to observations about the rates of reaction of coordination complexes. He saw some things that were unsurprising. He also drew some new conclusions based on ligand field theory.

Exercise \(\PageIndex{2}\)

In which compound from each pair would you expect the strongest ionic bonds? Why?

a) LiF vs KBr
b) CaCl₂ vs. KCl

Answer a

The ions in LiF are both smaller than in KBr, so the force of attraction between the ions in LiF is greater because of the smaller separation between the charges.

Answer b

Calcium has a 2+ charge in CaCl₂, whereas potassium has only a + charge, so the chloride ions are more strongly attracted to the calcium than to the potassium.

Taube observed that many M⁺¹ ions (M = metal) are more labile than many M⁺³ ions, in general. That isn't too surprising, since metal ions function as electrophiles or Lewis acids and ligands function as nucleophiles or Lewis bases in forming coordination complexes. In other words, metals with higher charges ought to be stronger Lewis acids, and so they should bind ligands more tightly. However, there were exceptions to that general rule. For example, Taube also observed that \(\ce{Mo+5}\) compounds are more labile than \(\ce{Mo+3}\) compounds. So, there must be more going on here than just the effects of electrostatic attraction.

Another factor that governs ionic bond strengths is the size of the ion. Typically, ions with smaller atomic radii form stronger bonds than ions with larger radii. Taube observed that Al³⁺, V³⁺, Fe³⁺ and Ga³⁺ ions are all about the same size. All these ions exchange ligands at about the same rate. That isn't surprising, because they have the same charge and the same radius.  However, Cr³⁺ is also about the same size as those ions and it also has the same charge, but it is much less labile. Once again, there are exceptions to our regular expectations based on simple electrostatic considerations. Furthermore, 4d and 5d transition metals (Y\(\rightarrow\)Cd, and Ac\(\rightarrow\)Hg) are much more inert than 3d transition metals (Sc\(\rightarrow\)Zn). This is unexpected when we consider size; the 4d and 5d metals are much larger than the 3d metals. This unexpected behavior tells us that electrostatics alone cannot predict lability.

Taube came up with a hypothesis that could explain the seeming contradictory oservations described above: kinetic lability must be affected by d-electron configuration. This idea forms the basis of Taube's rules about lability.

For example, metals like Ni²⁺ and Cu²⁺ are very labile. The d orbital splitting diagrams for those compounds would have d electrons in the e_g set. Remember, the e_g set arises from interaction with the ligand donor orbitals; this set corresponds to a \(\sigma\) antibonding level.

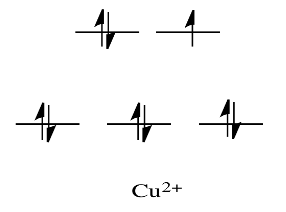
By comparison, V²⁺ is rather inert. The d orbital splitting diagram in this case has electrons in the t_2g set, but none in the e_g set.

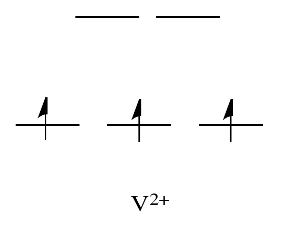
So, having electrons in the higher energy, antibonding e_g level weakens the bond to the ligand, so the ligand can be replaced more easily. In the absence of those higher energy electrons, the bond to the ligand is stronger, and the ligand isn't replaced as easily.

On the other hand, metals like Ca²⁺, Sc³⁺ and Ti⁴⁺ are pretty labile. The d orbital splitting diagrams in those cases are pretty simple: there are no d-electrons at all in these ions.

That means having no electrons in these mostly non-bonding levels leaves the complex susceptible to ligand replacement. But it's hard to see why population of an orbital that is mostly non-bonding would have an effect on ligand bond strength.

Instead, this factor probably has something to do with the part of ligand substitution that we have ignored so far. Not only does one ligand need to leave, but a second one needs to bond in its place. So, having an empty orbital for the ligand to donate electrons into (or, put another way, not having electrons in the way that may complicate donation from the ligand) makes that part of the reaction easier.

Exercise \(\PageIndex{3}\)

Consider all possible electron configurations for octahedral complexes (\(d^0\) to \(d^{10}\), high spin and low spin cases): predict whether each case would be inert, intermediate, or labile.

Answer

Exercise \(\PageIndex{4}\)

Put the metal ions in order of decreasing reaction rate (from labile to inert):

a) \(Al^{3+}, Na^+, Mg^{2+}\)

b) \(Ca^{2+}, Mg^{2+}, Sr^{2+} \)

Answer (a)

Most Labile to most inert: \(Na^+ >  Mg^{2+}  >  Al^{3+}\)

These are metal ions with similar size and varying charge. They are in order of increasing charge and increasing density from left to right.

Answer (b)

Most labile to most inert: \(Sr^{2+} > Ca^{2+} > Mg^{2+}\)

These metal ions have the same charge, and vary in size. They are in order of decreasing charge and increasing charge density from left to right.

Exercise \(\PageIndex{5}\)

Some metals, like Mn²⁺, can be either labile or inert, depending on whether they are high spin or low spin. Explain why using d orbital splitting diagrams.

Answer

Add texts here. Do not delete this text first.

Exercise \(\PageIndex{6}\)

Predict whether the following metals, in octahedral complexes, are labile or not.

a) Co³⁺ (high spin)

b) Co³⁺ (low spin)

c) Fe²⁺ (low spin)

d) Fe²⁺ (high spin)

e) Zn²⁺

Answer

Answer a

labile (electrons in higher energy d orbital set)

Answer b

not labile (all electrons in lower energy d orbitals)

Answer c

not labile (all electrons in lower energy d orbitals)

Answer d

labile (electrons in higher energy d orbital set)

Answer e

labile (electrons in higher energy d orbital set)

---

Overall Generalizations for Kinetics:

1. s-block metals are very labile, except for those with very high charge density (eg. \(Mg^{2+}\ is\:  inert\))
2. \(d^{10}\) metals are labile (eg: \(Zn^{2+}, Cu^+, Hg^{2+}\))
3. Other ions with a full shell are labile (eg: \(Ln^{3+}\) of f-block)
4. 3d \(M^{2+}\), when high spin, are generally labile (eg. \(Cu^{2+} is\:  very\:  labile\))
5. 4d and 5d are usually inert due to higher LFSE (low spin, high LFSE)
6. \(M^{2+}\) is more labile than the same metal as \(M^{3+}\)
7. \(d^3\) and low spin \(d^6\) are inert (eg. \(Cr^{3+}, Co^{3+}, \) low spin \(Fe^{2+}\))

---

Attribution

Chris P Schaller, Ph.D., (College of Saint Benedict / Saint John's University)

Curated or created by Kathryn Haas