8.1: Application of symmetry to carbonyl vibrational modes
- Page ID
- 276138
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
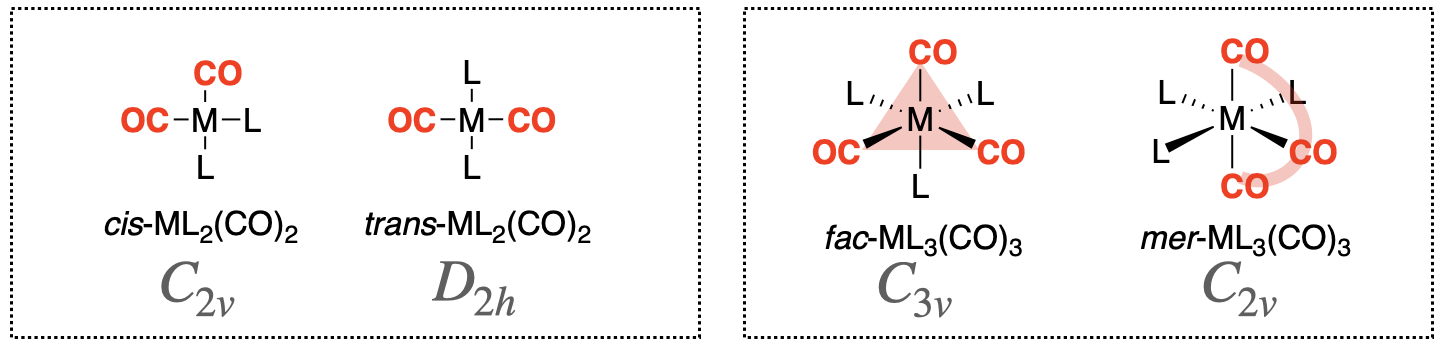
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The interpretation of CO stretching vibrations in an IR spectrum is particularly useful. Symmetry and group theory can be applied to predict the number of CO stretching bands that appear in a vibrational spectrum for a given metal coordination complex. A classic example of this application is in distinguishing isomers of metal-carbonyl complexes. For example, the cis- and trans- isomers of square planar metal dicarbonyl complexes (ML2(CO)2) have a different number of IR stretches that can be predicted and interpreted using symmetry and group theory. Another example is the case of mer- and fac- isomers of octahedral metal tricarbonyl complexes (ML3(CO)3). Structures of the two types of metal carbonyl structures, and their isomers are shown in Figure \(\PageIndex{1}\). The isomers in each case can be distinguished using vibrational spectroscopy.
EXAMPLE 1: Distinguishing cis- and trans- isomers of square planar metal dicarbonyl complexes
General structures of the cis- and trans- isomers of square planar metal dicarbonyl complexes (ML2(CO)2) are shown in the left box in Figure \(\PageIndex{1}\). We can use symmetry and group theory to predict how many carbonyl stretches we should expect for each isomer following the steps below.
Step 1: Assign the point group and Cartesian coordinates for each isomer.
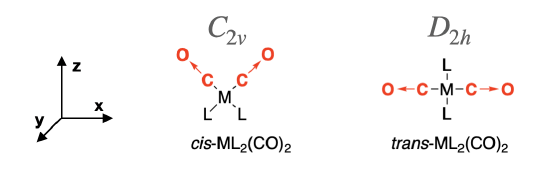
The cis-isomer has \(C_{2v}\) symmetry and the trans-isomer has \(D_{2h}\) symmetry. We assign the Cartesian coordinates so that \(z\) is colinear with the principle axis in each case. For the \(D_2{h}\) isomer, there are several orientations of the \(z\) axis possible. The axes shown in Figure \(\PageIndex{2}\) will be used here.
Step 2: Produce a reducible representation (\(\Gamma\)) for CO stretches in each isomer
First, assign a vector along each C—O bond in the molecule to represent the direction of C—O stretching motions, as shown in Figure \(\PageIndex{2}\) (red arrows →). These vectors are used to produce a \reducible representation (\(\Gamma\)) for the C—O stretching motions in each molecule. Using the symmetry operations under the appropriate character table, assign a value of 1 to each vector that remains in place during the operation, and a value of 0 if the vector moves out of place. There will be no occasion where a vector remains in place but is inverted, so a value of -1 will not occur.
cis- ML2(CO)2:
For cis- ML2(CO)2, the point group is \(C_{2v}\) and so we use the operations under the \(C_{2v}\) character table to create the \(\Gamma_{cis-CO}\). \[\begin{array}{|c|cccc|} \hline \bf{C_{2v}} & E & C_2 &\sigma_v (xz) & \sigma_v' (yz) \\ \hline \bf{\Gamma_{cis-CO}} & 2 & 0 & 2 & 0 \\ \hline \end{array}\]
trans- ML2(CO)2:
For trans- ML2(CO)2, the point group is \(D_{2h}\) and so we use the operations under the \(D_{2h}\) character table to create the \(\Gamma_{trans-CO}\). \[\begin{array}{|c|cccccccc|} \hline \bf{C_{2v}} & E & C_2(z) & C_2(y) &C_2(x) & i &\sigma(xy) & \sigma(xz) & \sigma(yz) \\ \hline \bf{\Gamma_{trans-CO}} & 2 & 0 & 0 & 2 & 0 & 2 & 2 & 0\\ \hline \end{array}\]
Step 3: Break each \(\Gamma\) into its component irreducible representations
Each \(\Gamma\) can be reduced using inspection or by the systematic method described previously.
In the case of the cis- ML2(CO)2, the CO stretching vibrations are represented by \(A_1\) and \(B_1\) irreducible representations: \[\begin{array}{|c|cccc|cc|} \hline \bf{C_{2v}} & E & C_2 &\sigma_v (xz) & \sigma_v' (yz) \\ \hline \bf{\Gamma_{cis-CO}} & 2 & 0 & 2 & 0 & & \\ \hline A_1 & 1 & 1 & 1 & 1 & z & x^2, y^2, z^2 \\ B_1 & 1 & -1 & 1 & -1 & x, R_y & xz \\ \hline \end{array} \label{c2v}\]
In the case of trans- ML2(CO)2, the CO stretching vibrations are represented by \(A_1\) and \(B_{3u}\) irreducible representations:
\[\begin{array}{|c|cccccccc|cc|} \hline \bf{C_{2v}} & E & C_2(z) & C_2(y) &C_2(x) & i &\sigma(xy) & \sigma(xz) & \sigma(yz) \\
\hline \bf{\Gamma_{trans-CO}} & 2 & 0 & 0 & 2 & 0 & 2 & 2 & 0 & & \\
\hline A_{g} & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & & x^2, \; y^2, \; z^2\\
B_{3u} & 1 & -1 & -1 & 1 & -1 & 1 & 1 & -1 & x & \\
\hline \end{array}\]
These irreducible representations correspond to the symmetries of only the selected C—O vibrations. Since these motions are isolated to the C—O group, they do not include any rotations or translations of the entire molecule, and so we do not need to find and subtract rotationals or translations (unlike the previous cases where all motions were considered).
Step 4: Determine which vibrational modes are IR-active and\or Raman-active
Apply the infrared selection rules described previously to determine which of the CO vibrational motions are IR-active and Raman-active. The two isomers of ML2(CO)2 are described below.
In the case of the cis- ML2(CO)2, the CO stretching vibrations are represented by \(A_1\) and \(B_1\) irreducible representations. The characters of both representations and their functions are shown above, in \ref{c2v} (and can be found in the \(C_{2v}\) character table). Under \(C_{2v}\), both the \(A_1\) and \(B_1\) CO vibrational modes are IR-active and Raman-active. Therefore, two bands in the IR spectrum and two bands in the Raman spectrum is possible.
In the case of the trans- ML2(CO)2, the CO stretching vibrations are represented by \(A_g\) and \(B_{3u}\) irreducible representations. The characters of both representations and their functions are shown above, in \ref{c2v} (and can be found in the \(D_{2h}\) character table). Under \(D_{2h}\), the \(A_g\) vibrational mode is is Raman-active only, while the \(B_{3u}\) vibrational mode is IR-active only. Therefore, only one IR band and one Raman band is possible for this isomer.
Summary
It is possible to distinguish between the two isomers of square planar ML2(CO)2 using either IR or Raman vibrational spectroscopy. The cis- ML2(CO)2 can produce two CO stretches in an IR or Raman spectrum, while the trans- ML2(CO)2 isomer can produce only one band in either type of vibrational spectrum. If a sample of ML2(CO)2 produced two CO stretching bands, we could rule out the possibility of a pure sample of trans-ML2(CO)2.
Exercise \(\PageIndex{1}\)
Repeat the steps outlined above to determine how many CO vibrations are possible for mer-ML3(CO)3 and fac-ML3(CO)3 isomers (see Figure \(\PageIndex{1}\)) in both IR and Raman spectra. Could either of these vibrational spectroscopies be used to distinguish the two isomers?
- Answer
-
Add texts here. Do not delete this text first.


