7.2: Identifying all IR- and Raman-active vibrational modes in a molecule
- Page ID
- 270407
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Symmetry and group theory can be applied to understand molecular vibrations. This is particularly useful in the contexts of predicting the number of peaks expected in the infrared (IR) and Raman spectra of a given compound.
We will use water as a case study to illustrate how group theory is used to predict the number of peaks in IR and Raman spectra.
How many IR and Raman peaks would we expect for \(H_2O\)?
To answer this question with group theory, a pre-requisite is that you assign the molecule's point group and assign an axis system to the entire molecule. By convention, the \(z\) axis is collinear with the principle axis, the \(x\) axis is in-plane with the molecule or the most number of atoms. It is a good idea to stick with this convention (see Figure \(\PageIndex{1}\)).
- What is the point group for \(H_2O\)? (click to see answer)
-
\(H_2O\) has the following operations: \(E\), \(C_2\), \(\sigma_v\), \(\sigma_v'\). The point group is \(C_{2v}\).
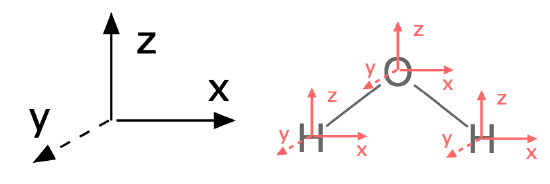
Figure \(\PageIndex{1}\): The first step to finding normal modes is to assign a consistent axis system to the entire molecule and to each atom. |
Now that we know the molecule's point group, we can use group theory to determine the symmetry of all motions in the molecule; the symmetry of each of its degrees of freedom. Then we will subtract rotational and translational degrees of freedom to find the vibrational degress of freedom. The number of degrees of freedom depends on the number of atoms (\(N\)) in a molecule. Each atom in the molecule can move in three dimensions (\(x,y,z\)), and so the number of degrees of freedom is three dimensions times \(N\) number of atoms, or \(3N\). The total degrees of freedom include a number of vibrations, three translations (in \(x\), \(y\), and \(z\)), and either two or three rotations. Linear molecules have two rotational degrees of freedom, while non-linear molecules have three. The vibrational modes are represented by the following expressions:
\[\begin{array}{ccc} \text{Linear Molecule Degrees of Freedom} & = & 3N - 5 \\ \text{Non-Linear Molecule Degrees of Freedom} & = & 3N-6 \end{array} \]
Our goal is to find the symmetry of all degrees of freedom, and then determine which are vibrations that are IR- and Raman-active.
STEP 1: Find the reducible representation for all normal modes \(\Gamma_{modes}\).
The first major step is to find a reducible representation (\(\Gamma\)) for the movement of all atoms in the molecule (including rotational, translational, and vibrational degrees of freedom). We'll refer to this as \(\Gamma_{modes}\). To find normal modes using group theory, assign an axis system to each individual atom to represent the three dimensions in which each atom can move. Each axis on each atom should be consistent with the conventional axis system you previously assigned to the entire molecule (see Figure \(\PageIndex{1}\)).
\(\Gamma_{modes}\) is the sum of the characters (trace) of the transformation matrix for the entire molecule (in the case of water, there are 9 degrees of freedom and this is now a 9x9 matrix). Let's walk through this step-by-step. The transformation matrix of \(E\) and \(C_2\) are shown below:
\[E=\begin{pmatrix} \color{red}1&0&0&0&0&0&0&0&0 \\ 0&\color{red}1&0&0&0&0&0&0&0 \\ 0&0&\color{red}1&0&0&0&0&0&0 \\0&0&0&\color{red}1&0&0&0&0&0 \\ 0&0&0&0&\color{red}1&0&0&0&0 \\ 0&0&0&0&0&\color{red}1&0&0&0 \\ 0&0&0&0&0&0&\color{red}1&0&0 \\ 0&0&0&0&0&0&0&\color{red}1&0 \\ 0&0&0&0&0&0&0&0&\color{red}1 \\ \end{pmatrix} \begin{pmatrix} x_{oxygen} \\ y_{oxygen} \\ z_{oxygen} \\ x_{hydrogen-a} \\ y_{hydrogen-a} \\ z_{hydrogen-a} \\ x_{hydrogen-b} \\ y_{hydrogen-b} \\ z_{hydrogen-b} \end{pmatrix} = \begin{pmatrix} x'_{oxygen} \\ y'_{oxygen} \\ z'_{oxygen} \\ x'_{hydrogen-a} \\ y'_{hydrogen-a} \\ z'_{hydrogen-a} \\ x'_{hydrogen-b} \\ y'_{hydrogen-b} \\ z'_{hydrogen-b} \end{pmatrix}, \chi=9 \nonumber\]
\[C_2=\begin{pmatrix} \color{red}-1&0&0&0&0&0&0&0&0 \\ 0&\color{red}-1&0&0&0&0&0&0&0 \\ 0&0&\color{red}1&0&0&0&0&0&0 \\0&0&0&\color{red}0&0&0&-1&0&0 \\ 0&0&0&0&\color{red}0&0&0&-1&0 \\ 0&0&0&0&0&\color{red}0&0&0&1 \\ 0&0&0&-1&0&0&\color{red}0&0&0 \\ 0&0&0&0&-1&0&0&\color{red}0&0 \\ 0&0&0&0&0&1&0&0&\color{red}0 \\ \end{pmatrix} \begin{pmatrix} x_{oxygen} \\ y_{oxygen} \\ z_{oxygen} \\ x_{hydrogen-a} \\ y_{hydrogen-a} \\ z_{hydrogen-a} \\ x_{hydrogen-b} \\ y_{hydrogen-b} \\ z_{hydrogen-b} \end{pmatrix} = \begin{pmatrix} x'_{oxygen} \\ y'_{oxygen} \\ z'_{oxygen} \\ x'_{hydrogen-a} \\ y'_{hydrogen-a} \\ z'_{hydrogen-a} \\ x'_{hydrogen-b} \\ y'_{hydrogen-b} \\ z'_{hydrogen-b} \end{pmatrix}, \chi=1 \nonumber\]
It is unnecessary to find the transformation matrix for each operation since it is only the TRACE that gives us the character, and any off-diagonal entries do not contribute to \(\Gamma_{modes}\). The values that contribute to the trace can be found simply by performing each operation in the point group and assigning a value to each individual atom to represent how it is changed by that operation. If the atom moves away from itself, that atom gets a character of zero (this is because any non-zero characters of the transformation matrix are off of the diagonal). If the atom remains in place, each of its three dimensions is assigned a value of \(\cos \theta\). For the example of \(H_2O\) under the \(C_{2v}\) point group, the axes that remain unchanged (\(\theta = 0^{\circ}\)) are assigned a value of \(\cos(0^{\circ})=1\), while those that are moved into the negative of themselves (rotated or reflected to \( \theta = 180^{\circ}\)) are assigned \(\cos(180^{\circ}) = -1\). The character for \(\Gamma\) is the sum of the values for each transformation.
Let's walk through the steps to assign characters of \(\Gamma_{modes}\) for \(H_2O\) to illustrate how this works:
For the operation, \(E\), performed on \(H_2O\), all three atoms remain in place. The three axes \(x,y,z\) on each atom remain unchanged. Thus, each of the three axes on each of three atom (nine axes) is assigned the value \(\cos(0^{\circ})=1\), resulting in a sum of \(\chi=9\) for the \(\Gamma_{modes}\).
For the operation, \(C_2\), the two hydrogen atoms are moved away from their original position, and so the hydrogens are assigned a value of zero. The oxygen remains in place; the \(z\)-axis on oxygen is unchanged (\(\cos(0^{\circ})=1\)), while the \(x\) and \(y\) axes are inverted (\(\cos(180^{\circ})\)). The sum of these characters gives \(\chi=-1\) in the \(\Gamma_{modes}\).
Now you try! Find the characters of \(\sigma_{v(xz)}\) and \(\sigma_{v(yz)}\) under the \(C_{2v}\) point group. Compare what you find to the \(\Gamma_{modes}\) for all normal modes given below.
\[\begin{array}{l|llll} C_{2v} & E & C_2 & \sigma_v & \sigma_v' \\ \hline \Gamma_{modes} & 9 & -1 & 3 & 1 \end{array} \label{gammamodes}\]
STEP 2: Break \(\Gamma_{modes}\) into its component irreducible representations.
Now that we've found the \(\Gamma_{modes}\) (\(\ref{gammamodes}\)), we need to break it down into the individual irreducible representations (\(i,j,k...\)) for the point group. We can do this systematically using the following formula:
\[\text{# of } i = \frac{1}{h}\sum(\text{# of operations in class)}\times(\chi_{\Gamma}) \times (\chi_i) \label{irs}\]
In other words, the number of irreducible representations of type \(i\) is equal to the sum of the number of operations in the class \(\times\) the character of the \(\Gamma_{modes}\) \(\times\) the character of \(i\), and that sum is divided by the order of the group (\(h\)).
Using equation \(\ref{irs}\), we find that for all normal modes of \(H_2O\):
\[\Gamma_{modes}=3A_1+1A_2+3B_1+2B_2 \label{water}\]
Notice their are 9 irreducible representations in equation \ref{water}. These irreducible representations represent the symmetries of all 9 motions of the molecule: vibrations, rotations, and translations.
Exercise \(\PageIndex{1}\): Derive the irreducible representation in equation \(\ref{water}\).
Derive the nine irreducible representations of \(\Gamma_{modes}\) for \(H_2O\), expression \(\ref{water}\).
- Hint
-
To find the number of each irreducible representation that combine to form the \(\Gamma_{modes}\), we need the characters of \(\Gamma{modes}\) that we found above (\(\ref{gammamodes}\)), the \(C_{2v}\) character table (below), and equation \(\ref{irs}\).
\(\begin{array}{l|llll|l|l} C_{2v} & {\color{red}1}E & {\color{red}1}C_2 & {\color{red}1}\sigma_v & {\color{red}1}\sigma_v' & \color{orange}h=4\\ \hline \color{green}A_1 & \color{green}1 & \color{green}1 & \color{green}1 & \color{green}1 & \color{green}z & \color{green}x^2,y^2,z^2\\ \color{green}A_2 & \color{green}1 & \color{green}1 & \color{green}-1 & \color{green}-1 & \color{green}R_z & \color{green}xy \\ \color{green}B_1 & \color{green}1 & \color{green}-1&\color{green}1&\color{green}-1 & \color{green}x,R_y & \color{green}xz \\ \color{green}B_2 & \color{green}1 & \color{green}-1 & \color{green}-1 & \color{green}1 & {\color{green}y} ,\color{green}R_x & \color{green}yz \end{array} \)
In the \(C_{2v}\) point group, each class has only one operation, so the number of operations in each class (from equation \(\ref{irs}\)) is \({\color{red}1}\) for each class. This has been explicitly added to the character table above for emphasis.
- Answer
-
The number of \(A_1\) = \(\frac{1}{\color{orange}4} \left[ ({\color{green}1} \times 9 \times {\color{red}1}) + ({\color{green}1} \times (-1) \times {\color{red}1}) + ({\color{green}1} \times 3 \times {\color{red}1}) + ({\color{green}1} \times 1 \times {\color{red}1})\right] = 3A_1 \)
The number of \(A_2\) = \(\frac{1}{\color{orange}4} \left[ ({\color{green}1} \times 9 \times {\color{red}1}) + ({\color{green}1} \times (-1) \times {\color{red}1}) + ({\color{green}(-1)} \times 3 \times {\color{red}1}) + ({\color{green}(-1)} \times 1 \times {\color{red}1})\right] = 1A_2 \)
The number of \(B_1\) = \(\frac{1}{\color{orange}4} \left[ ({\color{green}1} \times 9 \times {\color{red}1}) + ({\color{green}(-1)} \times (-1) \times {\color{red}1}) + ({\color{green}1} \times 3 \times {\color{red}1}) + ({\color{green}(-1)} \times 1 \times {\color{red}1})\right] = 3B_1 \)
The number of \(B_2\) = \(\frac{1}{\color{orange}4} \left[ ({\color{green}1} \times 9 \times {\color{red}1}) + ({\color{green}(-1)} \times (-1) \times {\color{red}1}) + ({\color{green}(-1)} \times 3 \times {\color{red}1}) + ({\color{green}1} \times 1 \times {\color{red}1})\right] = 2B_2 \)
STEP 3: Subtract rotations and translations to find vibrational modes.
Because we are interested in molecular vibrations, we need to subtract the rotations and translations from the total degrees of freedom.
\[\text{Vibrations } = \Gamma_{modes}-\text{ Rotations } - \text{ Translations }\]
In the example of \(H_2O\), the total degrees of freedom are given above in equation \(\ref{water}\), and therefore the vibrational degrees of freedom can be found by:
\[H_2O\text{ vibrations} = \left(3A_1 + 1A_2 + 3B_1 + 2B_2\right) - \text{ Rotations } - \text{ Translations } \label{watervib}\]
But which of the irreducible representations are ones that represent rotations and translations? The symmetry of rotational and translational degrees modes can be found by inspecting the right-hand columns of any character table. Rotational modes correspond to irreducible representations that include \(R_x\), \(R_y\), and \(R_z\) in the table, while each of the three translational modes has the same symmetry as the \(x\), \(y\) and \(z\) axes. For a non-linear molecule, subtract three rotational irreducible representations and three translations irreducible representations from the total \(\Gamma_{modes}\).
In the specific case of water, we refer to the \(C_{2v}\) character table:
\[\begin{array}{l|llll|l|l} C_{2v} & E & C_2 & \sigma_v & \sigma_v' & h=4\\ \hline A_1 &1 & 1 & 1 & 1 & \color{red}z & x^2,y^2,z^2\\ A_2 & 1 & 1 & -1 & -1 & \color{red}R_z & xy \\ B_1 &1 & -1&1&-1 & \color{red}x,R_y &xz \\ B_2 & 1 & -1 &-1 & 1 & \color{red}y ,R_x & yz \end{array} \nonumber \]
In \(C_{2v}\), translations correspond to \(B_1\), \(B_2\), and \(A_1\) (respectively for \(x,y,z\)), and rotations correspond to \(B_2\), \(B_1\), and \(A_1\) (respectively for \(R_x,R_y,R_z\)). Subtracting these six irreducible representations from \(\Gamma_{modes}\) will leave us with the irreducible representations for vibrations.
\[\begin{array}{lll} H_2O\text{ vibrations} &=& \Gamma_{modes} - \text{ Rotations } - \text{ Translations }\\ &=& \left(3A_1 + 1A_2 + 3B_1 + 2B_2\right) - (A_1 - B_1 - B_2) -(A_2 - B_1 - B_2) \\ &=& 2A_1 + 1B_1 \end{array} \]
The three vibrational modes for \(H_2O\) are \(2A_1 + 1B_1\). Note that we have the correct number of vibrational modes based on the expectation of \(3N-6\) vibrations for a non-linear molecule.
STEP 4: Determine which of the vibrational modes are IR-active and Raman-active.
The next step is to determine which of the vibrational modes is IR-active and Raman-active. To do this, we apply the IR and Raman Selection Rules below:
IR and Raman Selection Rules
Infrared selection rules:
If a vibration results in the change in the molecular dipole moment, it is IR-active. In the character table, we can recognize the vibrational modes that are IR-active by those with symmetry of the \(x,y\), and \(z\) axes.
In \(C_{2v}\), any vibrations with \(A_1\), \(B_1\) or \(B_2\) symmetry would be IR-active.
Raman selection rules:
If a vibration results in a change in the molecular polarizability. In the character table, we can recognize the vibrational modes that are Raman-active by those with symmetry of any of the binary products (\(xy\), \(xz\), \(yz\), \(x^2\), \(y^2\), and \(z^2\)) or a linear combination of binary products (e.g. \(x^2-y^2\)).
In \(C_{2v}\), any vibrations with \(A_1\), \(A_2\), \(B_1\) or \(B_2\) symmetry would be Raman-active.
In our \(H_2O\) example, we found that of the three vibrational modes, two have \(A_1\) and one has \(B_1\) symmetry. Both (\(A_1\) and \(B_1\) are IR-active, and both are also Raman-active. There are two possible IR peaks, and three possible Raman peaks expected for water.*
*It is important to note that this prediction tells only what is possible, but not what we might actually see in the IR and Raman spectra. For example, if the two IR peaks overlap, we might actually notice only one peak in the spectrum. Or, if one or more peaks is off-scale, we wouldn't see it in actual data. Group theory tells us what is possible and allows us to make predictions or interpretations of spectra.
Summary of Analysis for Water
Each molecular motion for water, or any molecule, can be assigned a symmetry under the molecule's point group. For water, we found that there are a total of 9 molecular motions; \(3A_1 + A_2 +3B_1 + 2B_2\). Six of these motions are not the translations and rotations. The remaining motions are vibrations; two with \(A_1\) symmetry and one with \(B_1\) symmetry.
We can tell what these vibrations would look like based on their symmetries. The two \(A_1\) vibrations must by completely symmetric, while the \(B_1\) vibration is antisymmetric with respect to the principle \(C_2\) axis.

| All Motions (step 2 above) | Translations (x,y,z) | Rotations (\(R_x,R_y,R_z\)) | Remaining Vibrations | Description of Vibration |
|---|---|---|---|---|
| \(3A_1\) | \(1A_1\) |
\(2A_1\) |
One is a symmetric stretch. The other is a symmetric bend. Both are IR-active and Raman-active | |
| \(A_2\) | \(1A_2\) | |||
| \(3B_1\) | \(1B_1\) | \(1B_1\) | \(1B_1\) | Antisymmetric stretch that is IR-active and Raman-active. |
| \(2B_2\) | \(1B_2\) | \(1B_2\) |
Exercise \(\PageIndex{1}\)
Find the symmetries of all motions of the square planar complex, tetrachloroplatinate (II). Determine which are rotations, translations, and vibrations. Determine which vibrations are IR and Raman active.
- Answer
-
Add texts here. Do not delete this text first.


