4.3.1: Polar bonds
- Page ID
- 243817
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Molecular orbital diagrams for heteronuclear diatomic molecules
The molecular orbital diagram of a heteronuclear diatomic molecule is approached in a similar way to that of homonuclear diatomic molecule. The orbital diagrams may also look similar. A major difference is that the more electronegative atom will have orbitals at a lower energy level. Two examples of heteronuclear diatomic molecules will be explored below as illustrative examples.
Carbon monoxide MO diagram
Carbon monoxide is an example of a heteronuclear diatomic molecule where both atoms are second-row elements. The valence molecular orbitals in both atoms are the \(2s\) and \(2p\) orbitals. The molecular orbital diagram for carbon monoxide (Figure \(\PageIndex{1}\)) is constructed similarly to how you would construct dicarbon or dioxygen, except that the oxygen orbitals have a lower potential energy than analogous carbon orbitals. The labeling of molecular orbitals in this diagram follows a convention by which orbitals are given serial labels according to type of orbital (\(\sigma\), \(\pi\), etc). The lowest energy orbitals of any type are assigned a value of 1 and higher energy orbitals of the same type are assigned by increasing intervals (..2, 3, 4...). The orbital labeling system described previously is inappropriate for heteronuclear diatomic molecules that cannot be assigned \(g\) and \(u\) subscripts.
A consequence of unequal atomic orbital energy levels is that orbital mixing is significant. Notice the order of the molecular orbitals labeled \(1\pi\) and \(3\sigma\) in Figure \(\PageIndex{1}\). This is a similar order of \(\pi\) and \(\sigma\) orbitals as we saw in the case of the \(\sigma_g\) and \(\pi_u\) orbitals of \(N_2\) and lighter diatomics of the second period. Because the oxygen \(2p_z\) orbital is close in energy to both the carbon \(2p_z\) and carbon \(2s\), these three orbitals will have significant interaction (mixing). The result is an increase in the energy of the \(3\sigma\) orbital and a decrease in energy of the \(2\sigma^*\) orbital, resulting in the diagram shown in Figure \(\PageIndex{1}\).
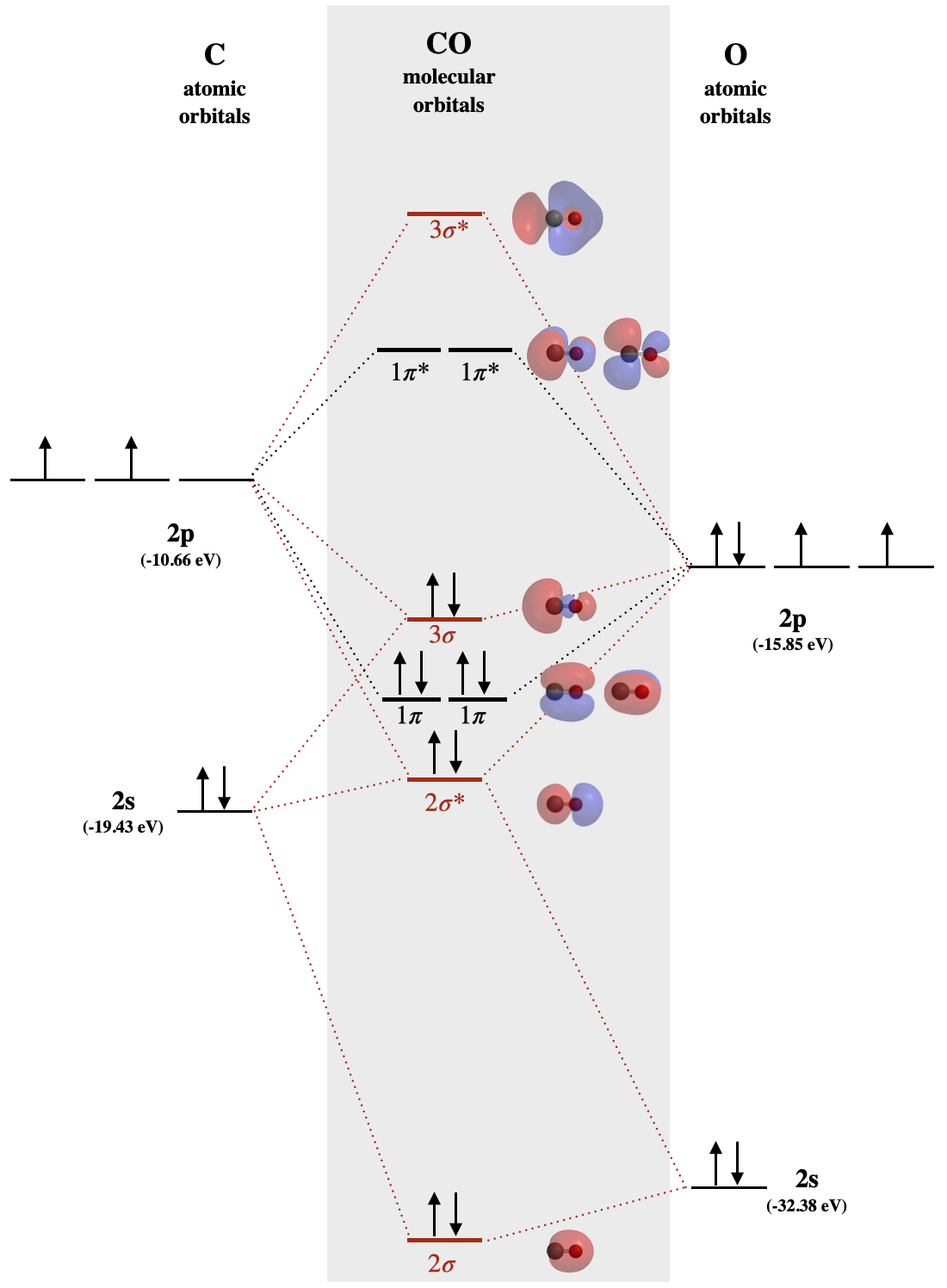
In the case of carbon monoxide (Figure \(\PageIndex{1}\)), atomic orbitals contribute unequally to each molecular orbital. For example, because the \(2s\) orbital of oxygen is very close in energy to the \(2\sigma\) moelcular orbital, it contributes to that molecular orbital more than the \(2s\) orbital from carbon. Notice the shape of this \(2\sigma\) orbital and how it is unevenly distributed over the two atoms; it is more heavily distributed on the oxygen because it is most like the oxygen \(2s\). This is in-line with the assumption that electron density is distributed more on oxygen because it is a more electronegative than carbon. Likewise, the \(1\pi\) orbitals are unevenly distributed, with more distribution close to the oxygen.
Exercise \(\PageIndex{1}\)
Examine the shape of the \(3\sigma\) orbital of carbon monoxide in Figure (\(\PageIndex{1}\)). Describe what ways this shape is different from the shape of the \(\sigma_g\) orbitals from second period homonuclear diatomic molecules (see Fig. 5.2.1.1). Rationalize these differences. Both orbitals are re-created below for convenience.

- Answer
-
The 3\(\sigma\) orbital is like the \(\sigma_g\) in that it has three lobes and two nodes distributed along the internuclear bond. They are different in their distribution. The two external lobes of \(\sigma_g\) are evenly distributed because the are an equal combination of two \(p_z\) orbitals (one from each atom). The \(3\sigma\) orbital is more heavily distributed toward the carbon atom, the less electronegative atom, than toward the oxygen. The unequal distribution of \(3\sigma\) is apparent in the unequal sizes of its exterior lobes, and the uneven shape of the interior lobe. The heavier distribution within the exterior lobe on carbon caused by the mixing of the carbon \(2s\) orbital with carbon and oxygen \(2p_z\) orbitals. The uneven shape of the interior lobe, where it leans toward oxygen, is best explained by the fact that the \(3\sigma\) orbital is closer in energy to the oxygen \(2p_z\) than the carbon \(2p_z\).
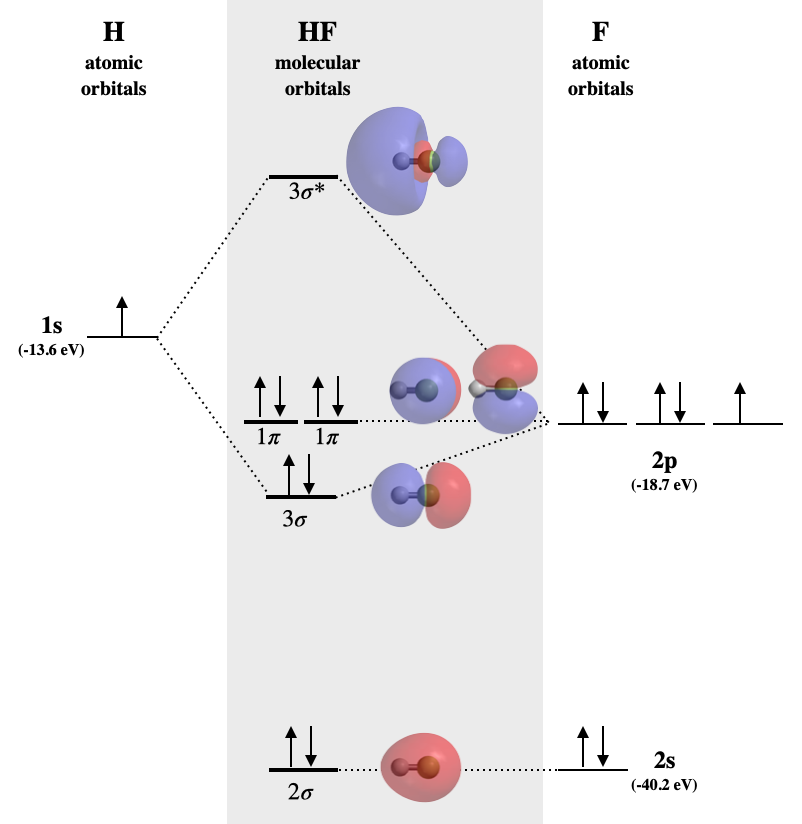
Hydrogen fluoride MO diagram
Hydrogen fluoride is an example of a heteronuclear diatomic molecule in which the two atoms are from different periods. In this case, the valence orbital of H is \(1s\) while those of F are \(2s\) and \(2p\). The molecular orbital diagram for HF is shown in Figure \(\PageIndex{2}\).
Three of these orbitals have compatible symmetry for mixing; these are the hydrogen \(1s\), fluorine \(2s\), and fluorine \(2p\). However, the extent to which they will interact depends on their relative energies. Fluorine is more electronegative than H, and the fluorine atom has a higher first ionization energy than does hydrogen. From these trends, we can expect that the fluorine valence orbitals are lower in energy than that of hydrogen. From Table 5.3.1, we find that the 1s orbital of H (-13.6 eV) is higher in energy than both fluorine orbitals (-18.7 and -40.2 eV, respectively for \(2p\) and \(2s\)). The energies of hydrogen \(1s\) and fluorine \(2p\) are a good match for combination, however, the \(2s\) orbital is much too different to create a productive interaction. Therefore, we expect that the fluorine \(2s\) will create a non-bonding molecular orbital, while the \(1s\) and \(2p_z\) orbital combine to make \(\sigma\) bonding and \(\sigma^*\) antibonding molecular orbitals. The remaining \(2p_x\) and \(2p_y\) orbitals do not have compatible symmetry for bonding with hydrogen, and they will form non-bonding \(\pi\) molecular orbitals. The non-bonding orbitals will have similar energy and character as their component atomic orbitals.
Chemical reactions take place at the HOMO and LUMO orbitals
Knowledge of molecular orbital diagrams, and the shapes of molecular orbitals, can be used to accurately explain and predict chemical reactivity. Chemical reactions take place using the highest occupied molecular orbitals (HOMO) of a nucleophile or Lewis base, and the lowest unoccupied molecular orbital (LUMO) of an electrophile or Lewis acid.
Lewis bases react using electrons in the HOMO, while Lewis acids react using the empty LUMO.
Example: Reactivity of CO with metal ions
CO is an excellent ligand for many metal ions. In fact, the strong affinity between CO and the heme iron (Fe) ions in hemoglobin can explain the mechanism of carbon monoxide poisoning. When CO binds in place of \(O_2\) to hemoglobin, that hemoglobin can no longer carry \(O_2\) to tissue cells. CO binding to hemoglobin is strong and practically irreversible. When CO binds to metal ions, it does so through the carbon atom. This is contrary to expectations based on the Lewis structure and the known bond polarity, where electron density is polarized toward oxygen. The distribution of the electron density of the HOMO of CO can explain this observation!
Exercise \(\PageIndex{2}\)
Refer to the MO diagram for CO. Identify the HOMO and explain why CO bonds to metal ions through the carbon atom rather than through the oxygen atom.
- Answer
-
Add texts here. Do not delete this text first.
Curated or created by Kathryn Haas


