4.2.1: Molecular Orbitals

Last updated
Save as PDF

Page ID: 241397

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

There are several cases where our more elementary models of bonding (like Lewis Theory and Valence Bond Theory) fail to predict the actual molecular properties and reactivity. A classic example is the case of \(O_2\) and its magnetic properties. At very cold temperatures, \(O_2\) is attracted to a magnetic field, and thus it must be paramagnetic (unpaired electrons give rise to magnetism, see video). However, both its Lewis structure and Valance Bond Theory predict that \(O_2\) is diamagnetic.

The magnetic properties of \(O_2\) are easily rationalized by its molecular orbital diagram. A molecular orbital diagram is a diagram that shows the relative energies and identities of each molecular orbital in a molecule. Figure \(\PageIndex{1}\) shows a simplified and generic molecular orbital diagram for a second-row homonuclear diatomic molecule. The diagram is simplified in that it assumes that interactions are limited to degenerate orbitals from two atoms (see next section).

There are some things you should note as you inspect Figure \(\PageIndex{1}\), and these are things you should consider as you draw your own molecular orbital diagrams. First, notice that there are the same number of molecular orbitals as there are atomic orbitals. Second, notice that each orbital in the diagram is rigorously labeled using labels (\(\sigma\) and \(\pi\)) that include the subscripts \(u\) and \(g\). These labels and subscripts indicate the symmetry of the orbitals. The \(\sigma\) symbol indicates the orbital is symmetric with respect to the internuclear axis, while the \(\pi\) label indicates that there is one node along that axis. The \(g\) and \(u\), stand for gerade and ungerade, the German words for even and uneven, respectively. The subscript \(g\) is given to orbitals that are even, or symmetric, with respect to an inversion center. The subscript \(u\) is given to orbitals that are uneven, or antisymetric, with respect to an inversion center. The pictures of calculated molecular orbitals are shown to illustrate the symmetry of each orbital.

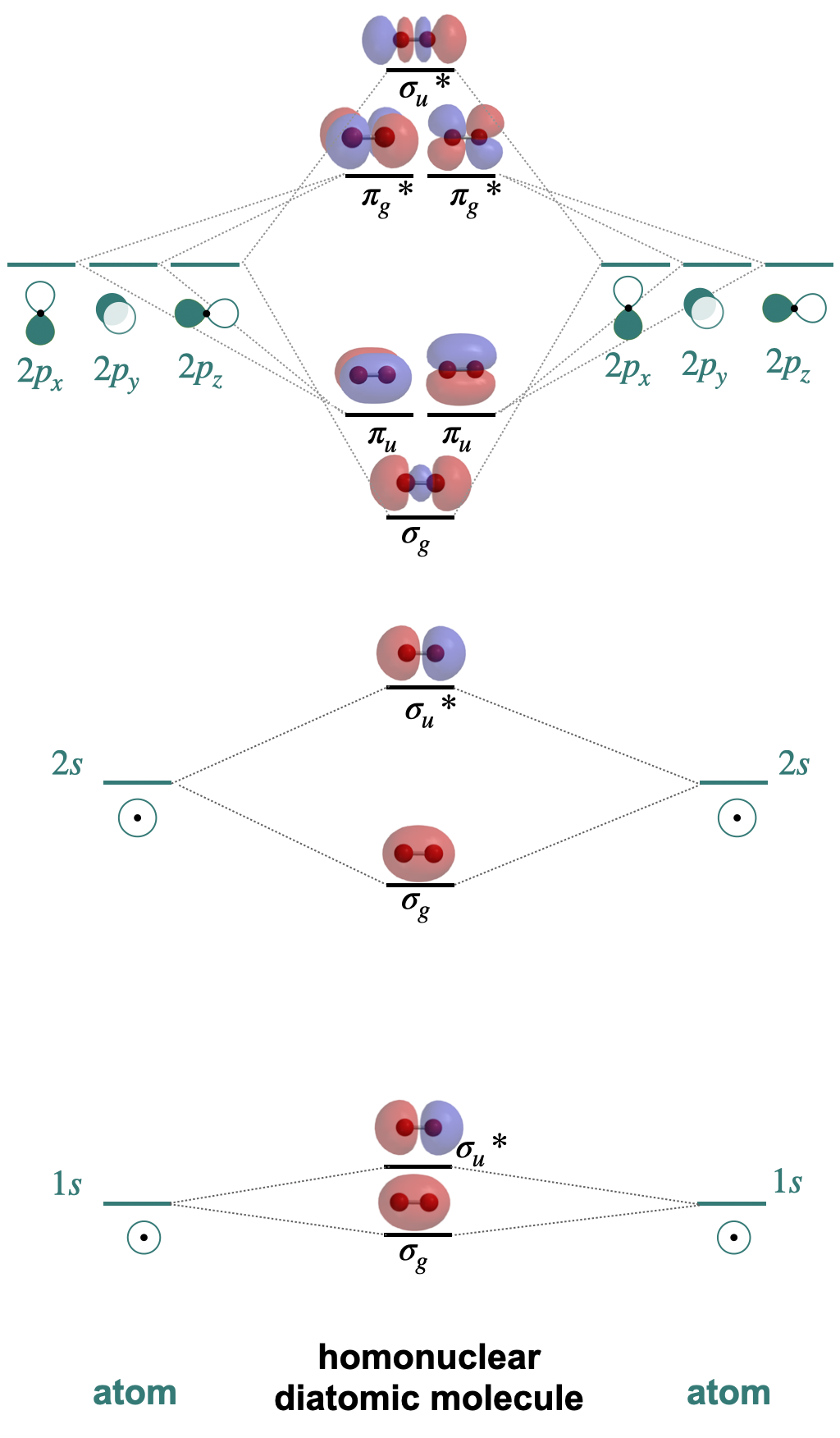
Screen Shot 2020-07-23 at 11.50.27 AM.png — Figure \(\PageIndex{1}\): A molecular orbitals diagram for second-row elements assuming no orbital mixing (interactions are formed by orbitals from each atom of the same energy).

Another important thing to notice is that the diagram in Figure \(\PageIndex{1}\) lacks electrons (because it is generic for any second-row diatomic molecule). If this were a complete molecular orbital diagram it would include the electrons for each atom and for the molecule. Electrons in molecular orbitals are filled in the same way an atomic orbital diagram would be filled, where electrons occupy lower energy orbitals before higher energy orbitals, and electrons occupy empty degenerate orbitals before pairing. A complete molecular orbital diagram would show whether the molecule is diamagnetic or paramagnetic. It can also be used to calculate the bond order of the molecule (the number of bonds between atoms) using the formula below:

\[\text{Bond order } =\frac{1}{2}\left[\left(\begin{array}{c}\text { number of electrons } \\ \text { in bonding orbitals }\end{array}\right)-\left(\begin{array}{c}\text { number of electrons } \\ \text { in antibonding orbitals }\end{array}\right)\right]\]

In general, non-valence electrons can be ignored because they contribute nothing to the bond order. In fact, many molecular orbital diagrams will ignore the core orbitals due to the fact they are insignificant for bonding interactions and reactivity.

Curated or created by Kathryn Haas