1.3: Introduction to Kinetic and Potential Energy
- Page ID
- 15523
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Define energy and its two main types listed below
- Describe the conservation of energy
Energy is the capacity to do work. You have a sense of what work is from regular life, it's things that require effort. Energy and work have the same units.
Kinetic Energy
At the end of the seventeenth century, a quantity was introduced into mechanics to explain collisions between two perfectly elastic bodies, in which one body makes a head-on collision with an identical body at rest. The first body stops, and the second body moves off with the initial velocity of the first body. (If you have ever played billiards or croquet, or seen a model of Newton’s Cradle, you have observed this type of collision.) The idea behind this quantity was related to the forces acting on a body and was referred to as “the energy of motion.” Later on, during the eighteenth century, the name kinetic energy was given to energy of motion.

The equation for kinetic energy is
$$KE=\frac{1}{2}mv^{2} \label{7.6}$$
where \(KE\) is kinetic energy, \(m\) is mass, and \(v\) is velocity. This definition should make sense: big things moving fast have the most energy, the most ability to shove other things or knock them over, etc.
Example \(\PageIndex{1}\): Kinetic Energy of an Object
- What is the kinetic energy of an 80-kg athlete, running at 10 m/s?
- The Chicxulub crater in Yucatan, one of the largest existing impact craters on Earth, is thought to have been created by an asteroid, traveling at 22 km/s and releasing 4.2 x 1023 J of kinetic energy upon impact. What was its mass?
- In nuclear reactors, thermal neutrons, traveling at about 2.2 km/s, play an important role. What is the kinetic energy of such a particle?
Strategy
To answer these questions, you can use the definition of kinetic energy in Equation \(\ref{7.6}\). You also have to look up the mass of a neutron.
Solution
Do not forget to convert km into m to do these calculations, although, to save space, we omitted showing these conversions.
- $$KE = \frac{1}{2} (80\; kg)(10\; m/s)^{2} = 4.0\; kJ \ldotp \nonumber $$
- $$m = \frac{2K}{v^{2}} = \frac{2(4.2 \times 10^{23}\; J)}{22\; km/s)^{2}} = 1.7 \times 10^{15}\; kg \ldotp \nonumber$$
- $$KE = \frac{1}{2} (1.68 \times 110^{-27}\; kg) (2.2\; km/s)^{2} = 4.1 \times 10^{-21}\; J \ldotp \nonumber$$
Significance
In this example, we used the way mass and speed are related to kinetic energy, and we encountered a very wide range of values for the kinetic energies. Different units are commonly used for such very large and very small values. The energy of the impactor in part (b) can be compared to the explosive yield of TNT and nuclear explosions, 1 megaton = 4.18 x 1015 J. The Chicxulub asteroid’s kinetic energy was about a hundred million megatons. At the other extreme, the energy of subatomic particle is expressed in electron-volts, 1 eV = 1.6 x 10−19 J. The thermal neutron in part (c) has a kinetic energy of about one fortieth of an electronvolt.
Exercise \(\PageIndex{1}\)
- A car and a truck are each moving with the same kinetic energy. Assume that the truck has more mass than the car. Which has the greater speed?
- A car and a truck are each moving with the same speed. Which has the greater kinetic energy?
Potential Energy
Potential energy is energy that comes from position. There are many different flavors of potential energy with two discussed below.
Gravitational Potential Energy
Gravitational potential energy is the energy that objects that are "high up" in a gravitation field (e.g., surface of earth). The equation for potential energy from gravity is
$$PE=mgh \label{pe1}$$
where \(PE\) is potential energy, \(m\) is mass, \(g\) is the acceleration of gravity, and \(h\) is the height. This makes the units of energy very clear:
\[\text{mass} \times \text{distance} \times \text{acceleration} \nonumber\]
or
\[\text{force}\times \text{distance} \nonumber\]
which both comes to units of kg•m2s-2.
Example \(\PageIndex{2}\)
A 15 gram ball sits on top of a 2m high refrigerator. What is the potential energy of the ball at the top of the refrigerator?
Solution
Use equation for gravitational potential energy (Equation \ref{pe1}) with mass =15 grams. This mass however has to be in kilograms. The conversion to grams to kilograms is:
- 1,000 grams per 1 kg
- height=2
- g=9.8
\[PE=(0.015)(9.8)(2)=0.294\, J \nonumber\]
Exercise \(\PageIndex{2A}\)
How much, in grams, does a cart full of groceries sitting on top of a 2 m hill weigh if its PE is 0.3 J?
- Answer
-
\[\begin{align*} 0.3 &= m (9.8)(2) \\[4pt] m&=0.015 kg \\[4pt] &=15\, g\end{align*}\]
Exercise \(\PageIndex{2B}\)
A 200 gram weight is placed on top of a shelf with a potential energy of 5 J. How high is the weight?
- Answer
-
\[\begin{align*} 5 &=\left(\dfrac{200}{1000}\right)(9.8)(h) \\[4pt] h &=2.55\, m \end{align*}\]
Coulombic Potential Energy
In chemistry, the force that leads to potential energy is almost always the Coulomb force, not gravity. The PE of two charged particles at a distance can be found through the equation:
\[E= \dfrac{q_1 q_2}{4π \epsilon_o r}\]
- \(r\) is distance
- \(q_1\) and \(q_2\) are the charges
- \(\epsilon_o\) is \(8.85 \times 10^{-12}\, C^2/J\,m\)
When the charges have the same sign, they repel and will accelerate away from each other if allowed to move; the potential energy has a positive sign. When the charges have the opposite sign, they attract each other and have negative potential energy. If they are allowed to get closer together, the potential energy will get more negative. If they are separated, \(r\) gets bigger and the potential energy approaches zero.
For charges with the same sign, \(E\) has a + sign and tends to get smaller as \(r\) increases. This can explain why like charges repel each other. Systems prefer a low PE and thus repel each other which increases the distance between them (\(r\)) and lowers the PE.
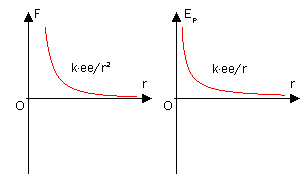
For charges with different charges, the opposite of what is stated above is true. \(E\) has a - sign which becomes even more negative as the opposite charged particles attract, or come closer together.
Example \(\PageIndex{3}\)
Calculate the potential energy of two particles with charges of \(3 \times 10^{-6}\,C\) and \(3.9 \times 10^{-6}\,C\) are separated by a distance of \(1\,m\).
Solution
\[\begin{align*} E&= \dfrac{(3 \times 10^{-6})(3.9\times 10^{-6})}{4π 8.85 \times 10^{-12}} \\[4pt] E&=0.105\, J \end{align*}\]
Exercise \(\PageIndex{3}\)
Find the distance between two particles that have a PE of 0.2 J and charges of \(2.5\times 10^{-6}\, C\) and \(3.1 \times 10^{-6}\, C\).
- Answer
-
\[\begin{align*} 0.2\,J &= \dfrac{(2.5 \times 10^{-6 })(3.1 \times 10^{-6})}{4 \pi 8.85 \times 10^{-12}r}) \\[4pt] &=\dfrac{(8.99 \times 10^9)(7.75 \times 10^{-11})}{r} \\[4pt] &=\dfrac{0.6967}{r} \end{align*}\]
cross multiply and solve for \(r\)
\[r=3.5\,m \nonumber\]
Conservation of Energy
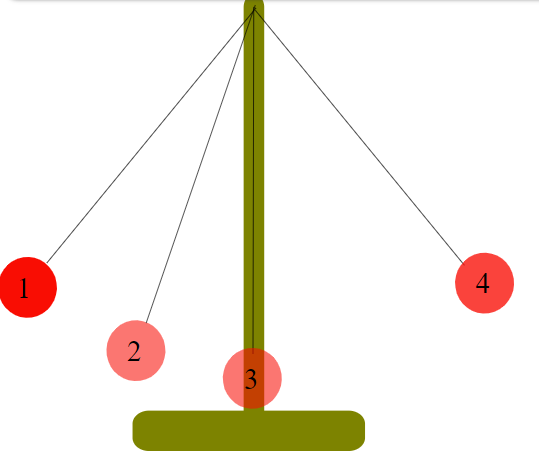
You probably learned about conservation of energy already in a physics class. For instance, if you have a pendulum as shown, at Position 1 the weight has some potential energy, but no kinetic energy. When you release the weight, the weight falls, moving through Position 2. At Position 2, some of the potential energy has been converted to kinetic energy. Finally, at Position 3, all the potential energy has been converted to kinetic energy. As it passes 3, the process is reversed, and kinetic energy is converted to potential energy. When the weight reaches Position 4, all the kinetic energy has been converted back to the same amount of potential energy it started with at 1. This is just one example of conservation of energy. It is a general observation that the amount of energy in the universe doesn't change, and the amount of energy in a particular system doesn't change unless there is a flow of energy in or out.
Contributors
Emily V Eames (City College of San Francisco)
- Brittanie Harbick (UCD), Laura Suh (UCD), Amrit Paul Bains (UCD)
- Kinetic Energy by OpenStax (CC BY 4.0).

