5.5: Hammond’s Postulate
- Page ID
- 225788
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objective
After completing this section, you should be able to use the Hammond postulate to explain the formation of the most stable carbocation during the addition of a protic acid, HX, to an alkene.
Now, back to transition states. Chemists are often very interested in trying to learn about what the transition state for a given reaction looks like, but addressing this question requires an indirect approach because the transition state itself cannot be observed. In order to gain some insight into what a particular transition state looks like, chemists often invoke the Hammond postulate, which states that a transition state resembles the structure of the nearest stable species. For an exergonic reaction, therefore, the transition state resembles the reactants more than it does the products.
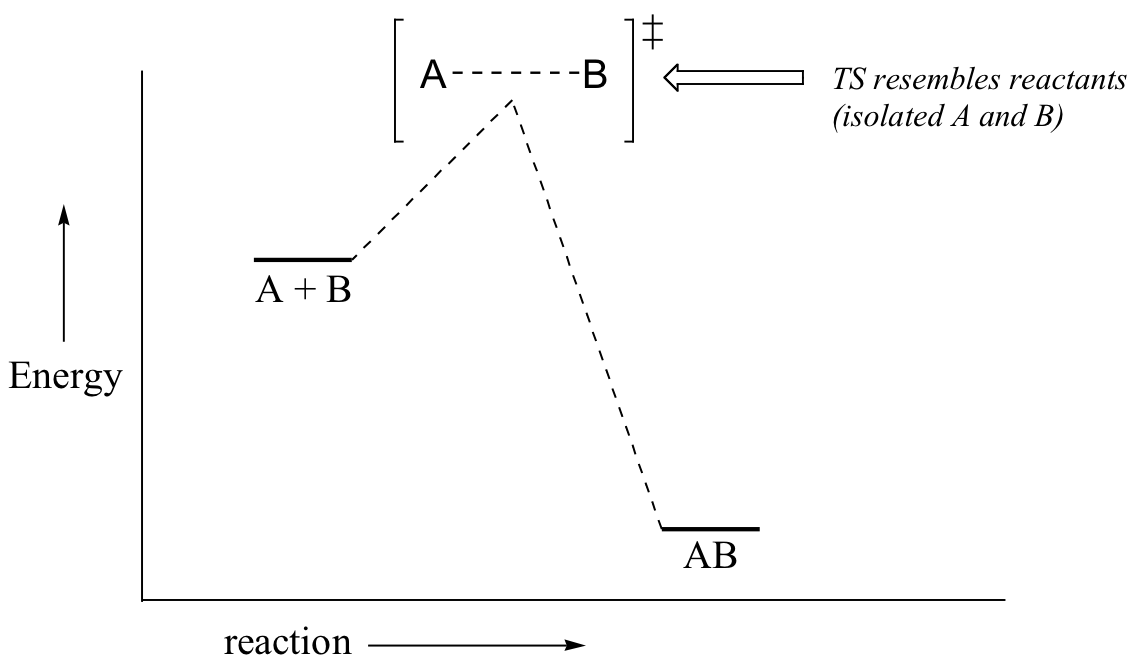
If we consider a hypothetical exergonic reaction between compounds A and B to form AB, the distance between A and B would be relatively large at the transition state, resembling the starting state where A and B are two isolated species. In the hypothetical endergonic reaction between C and D to form CD, however, the bond formation process would be much further along at the TS point, resembling the product.
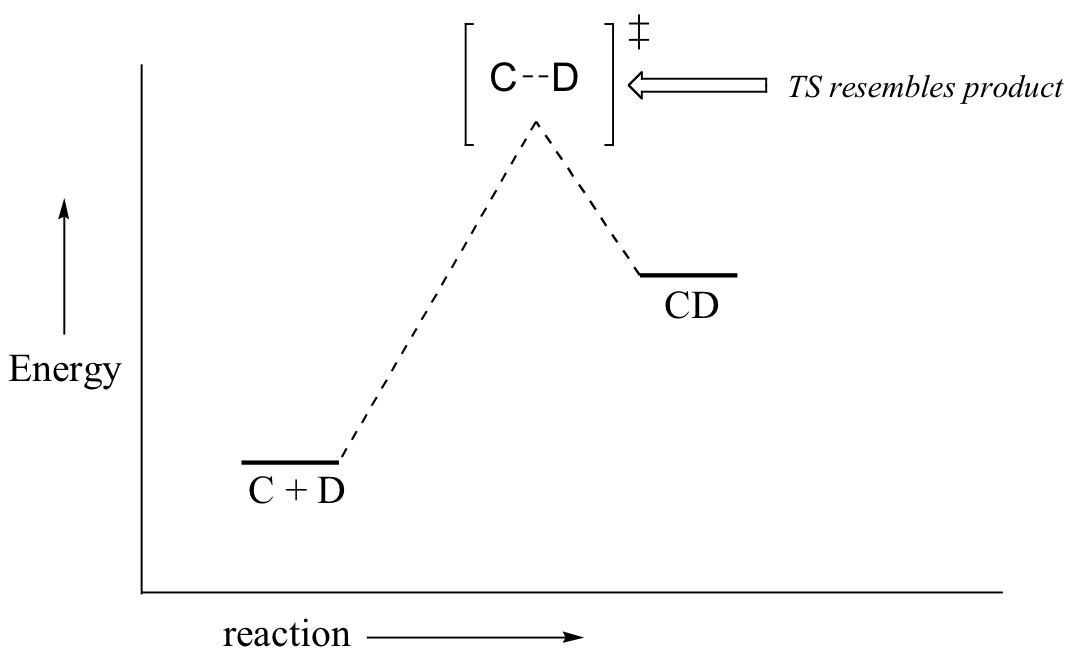
The Hammond Postulate is a very simplistic idea, which relies on an assumption that potential energy surfaces are parabolic. Although such an assumption is not rigorously true, it is fairly reliable and allows chemists to make energetic arguments about transition states by employing arguments about the stability of a related species. Since the formation of a reactive intermediate is very reliably endergonic, arguments about the stability of reactive intermediates can serve as proxy arguments about transition state stability.
The Hammond Postulate and the SN1 Reaction
Now, let’s turn our attention to a two-step reaction mechanism, such as an SN1 reaction between hydroxide and 2-chloro-2-methylpropane, which we will refer to as tert-butyl chloride. The energy diagram looks somewhat different:
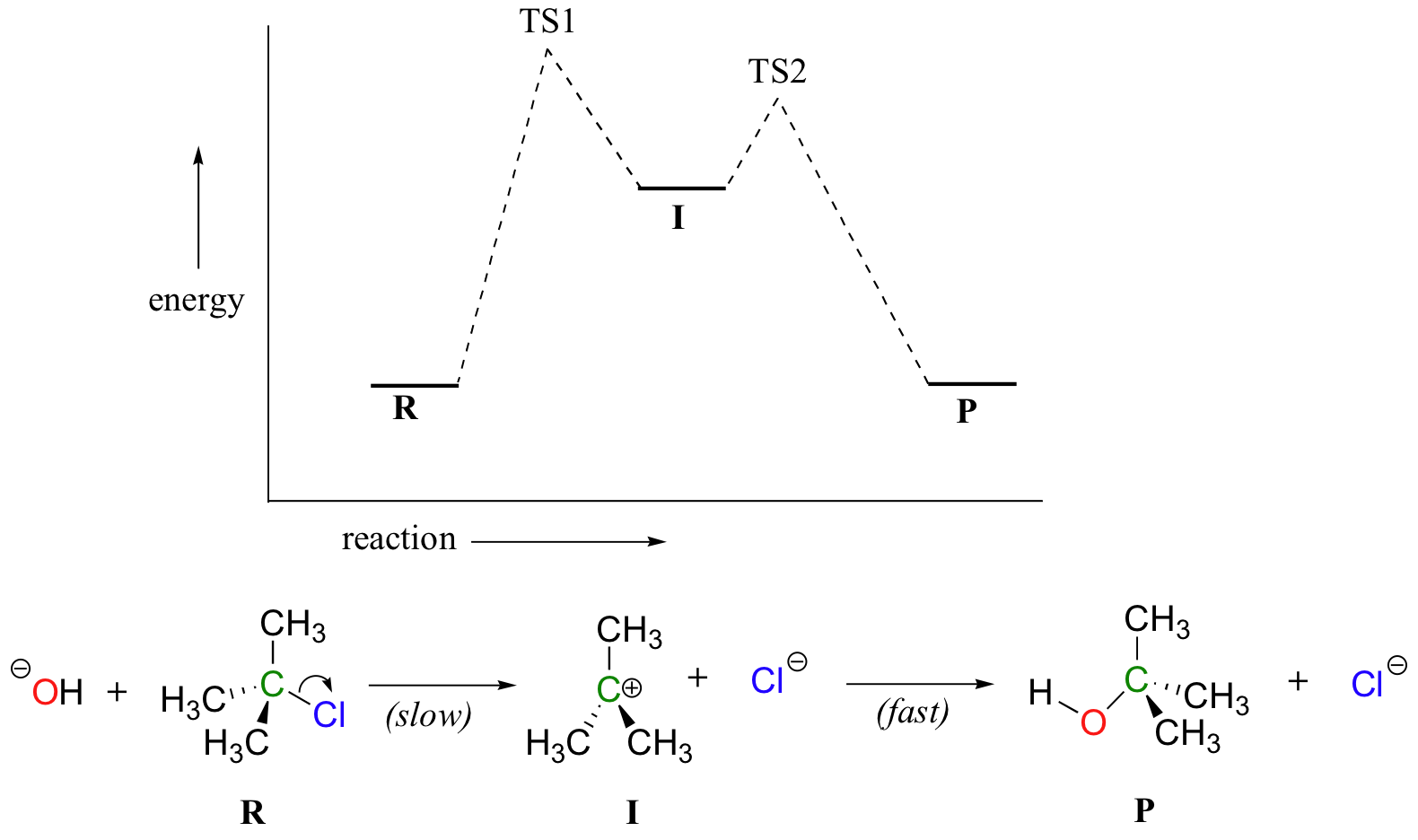
(NOTE: In practice, an SN1 reaction like this is difficult to perform in the lab under such strongly basic conditions with an alkyl halide, but it provides a nice, simple case with which to illustrate the kinetics.)
Because there are two steps involved, there are also two transition states and two activation energies to consider, as well as the carbocation intermediate. The first, bond-breaking step from R to I can be depicted as a highly endergonic reaction, because the carbocation-chloride ion pair is significantly less stable (higher in energy) than the starting state. The transition state for this step, labeled TS1, can be thought of as that point at which the carbon-chlorine bond is halfway broken. The second step, attack on the carbocation electrophile by the hydroxide nucleophile and formation of the new carbon-oxygen bond, is a highly exergonic step that passes through a second, much lower transition state TS2. The intermediate (I) is thus depicted as an energy valley situated between TS1 and TS2. According to Hammond’s postulate, both TS1 and TS2 in this reaction should resemble the intermediate I more than either the reactants or products, because in both cases the intermediate is the structure that is closest in energy. This idea – that an intermediate species resembles the nearby transition states – is a very important point to keep in mind, and we will revisit it several times throughout this text as we consider various organic reaction mechanisms.
There is one more very important idea expressed by the energy diagram that relates to the kinetics of the reaction. The activation energy for step 1 is much higher than the activation energy for step 2, meaning that step 1 is slower than step 2. This should make intuitive sense, because step 1 involves bond-breaking and separation of charge, while step 2 involves bond-forming and neutralization of charge. Because step 1 is slow and step 2 is fast, the overall rate of the reaction depends only on the rate of step 1. Step 1 is the ‘rate-determining step’; it is the bottleneck for the overall process. Anything that speeds up the rate of step 2 will not have any effect on the overall rate of the reaction.
Notice also that the rate-determining step involves only one of the two reactants: tert-butyl chloride breaks apart in this step, while hydroxide is not involved at all (contrast this to the SN2 reaction, where the single concerted step involves the collision of two species). The SN1 reaction has first order kinetics, and the rate depends only on the rate constant k and the concentration of tert-butyl chloride:
rate = k[tert-butyl chloride]
What this means is that if we double the rate of tert-butyl chloride, the rate of the reaction will also double. Doubling the hydroxide ion concentration, however, will have no effect on the rate, because hydroxide only participates in the fast, non-rate-determining step.
When thinking about any chemical reaction, it is very important not to confuse the two fundamental chemical concepts of thermodynamics and kinetics. A ‘downhill’, energy-releasing reaction can have a low activation energy and be very fast (our HCl + OH– example is a good case in point). A downhill reaction could also have a high activation energy and be very slow. Think of sugar: you know that sucrose is a high energy molecule and that you obtain lots of energy when you eat it and convert it to carbon dioxide and water, but you also know that sugar sitting in a bowl does not just spontaneously dissipate into carbon dioxide and water before your eyes. This process, although downhill in terms of thermodynamics, occurs very slowly in the absence of heat or catalysts.
As we have seen, the Hammond postulate suggests that the activation energy of the rate-determining first step will be inversely proportional to the stability of the carbocation intermediate. The stability of carbocations was discussed earlier, and a qualitative relationship is given below:
| Carbocation type | methyl | 1o alkyl | 2o alkyl | allylic | benzylic | 3o alkyl | |||||
| Carbocation stability | CH3(+) | < | CH3CH2(+) | < | (CH3)2CH(+) | ≈ | CH2=CH-CH2(+) | < | C6H5CH2(+) | ≈ | (CH3)3C(+) |
Consequently, we expect that 3º-alkyl halides will be more reactive than their 2º and 1º-counterparts in reactions that follow an SN1 mechanism. This matches with experiment for SN1 reactions, but is opposite to the reactivity order observed for the SN2 mechanism. Allylic and benzylic halides are exceptionally reactive by either mechanism.
- The Hammond Postulate. Authored by: Dr. Dietmar Kennepohl, Prof. Steven Farmer, William Reusch, Tim Soderbergu00a0. Located at: https://chem.libretexts.org/LibreTexts/Athabasca_University/Chemistry_350%3A_Organic_Chemistry_I/Chapter_7%3A_Alkenes%3A_Structure_and_Reactivity/7.10_The_Hammond_Postulate. Project: Chemistry LibreTexts. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike

