5.4: Kinetics

Now, let’s move to kinetics. Look again at the energy diagram for exergonic reaction: although it is ‘downhill’ overall, it isn’t a straight downhill run.

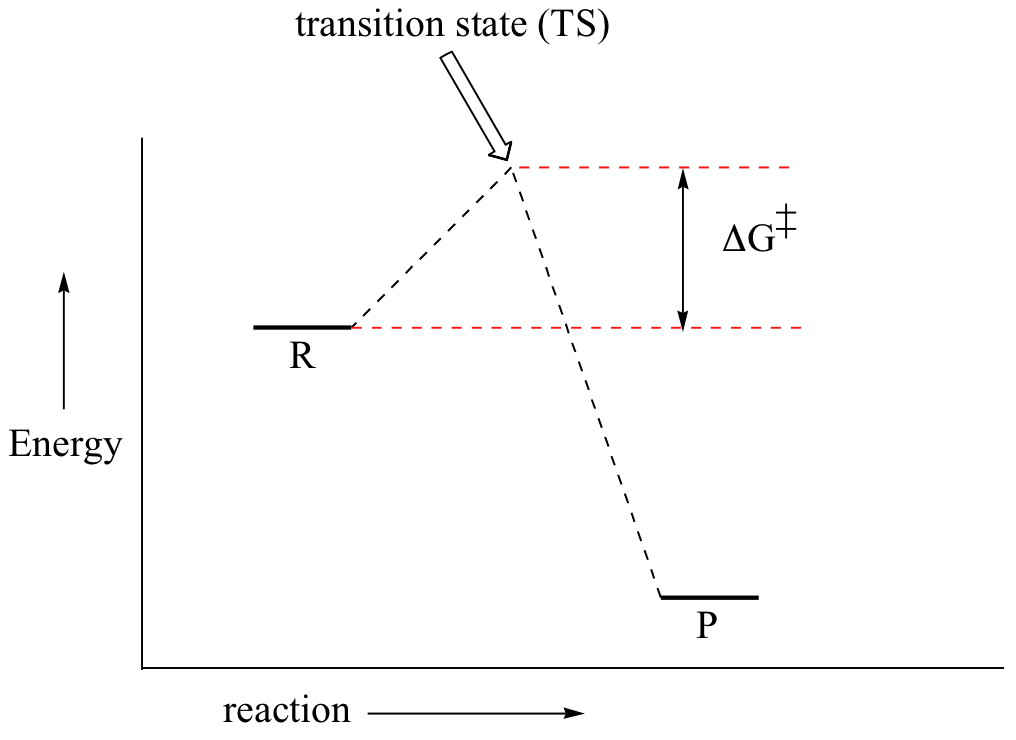
First, an ‘energy barrier’ must be overcome to get to the product side. The height of this energy barrier, you may recall, is called the ‘activation energy’ (ΔG^‡). The activation energy is what determines the kinetics of a reaction: the higher the energy hill, the slower the reaction.  At the very top of the energy barrier, the reaction is at its transition state (TS), which is the point at which the bonds are in the process of breaking and forming. The transition state is an ‘activated complex’: a transient and dynamic state that, unlike more stable species, does not have any definable lifetime. It may help to imagine a transition state as being analogous to the exact moment that a baseball is struck by a bat. Transition states are drawn with dotted lines representing bonds that are in the process of breaking or forming, and the drawing is often enclosed by brackets. Here is a picture of a likely transition state for our simple S_N2 reaction between hydroxide and chloromethane:

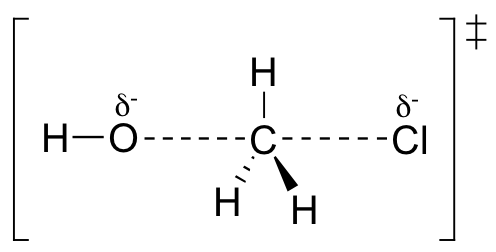
The S_N2 reaction involves a collision between two molecules: for this reason, we say that it has second order kinetics (this is the source of the number ‘2’ in S_N2).  The rate expression for this type of reaction is:

rate = k[reactant 1][reactant 2]

. . . which tells us that the rate of the reaction depends on the rate constantk as well as on the concentration of both reactants. The rate constant can be determined experimentally by measuring the rate of the reaction with different starting reactant concentrations. The rate constant depends on the activation energy, of course, but also on temperature: a higher temperature means a higher k and a faster reaction, all else being equal.  This should make intuitive sense: when there is more heat energy in the system, more of the reactant molecules are able to get over the energy barrier.

This study of reaction rates and the reaction coordinate diagram turns out to be invaluable for determining the mechanism for a reaction.  The mechanism tells us how the bonds are broken and made, and shows what intermediates (if any) are formed along the way.

Key Takeaways

• The rate determining step is the slowest one – the one with the highest energy barrier
• The rate of the rate determining step is equal to the rate for the overall reaction

Catalysis

We come now to the subject of catalysis.  Our hypothetical bowl of sugar (from end of the previous section)  is still stubbornly refusing to turn into carbon dioxide and water, even though by doing so it would reach a much more stable energy state.  There are, in fact, two ways that we could speed up the process so as to avoid waiting several millennia for the reaction to reach completion.  We could supply enough energy, in the form of heat from a flame, to push some of the sugar molecules over the high energy hill.  Heat would be released from the resulting exothermic reaction, and this energy would push more molecules over their energy hills, and so on – the sugar would literally burn up.A second way to make the reaction go faster is to employ a catalyst.  You probably already know that a catalyst is an agent that causes a chemical reaction to go faster by lowering its activation energy.

Enzymes – nature’s catalysts

How might you catalyze the conversion of sugar to carbon dioxide and water?  It’s not too hard – just eat the sugar, and let your digestive enzymes go to work catalyzing the many biochemical reactions involved in breaking it down.  Enzymes are proteins, and are very effective catalysts.  ‘Very effective’ in this context means very specific, and very fast.  Most enzymes are very selective with respect to reactant molecules: they have evolved over millions of years to catalyze their specific reactions. 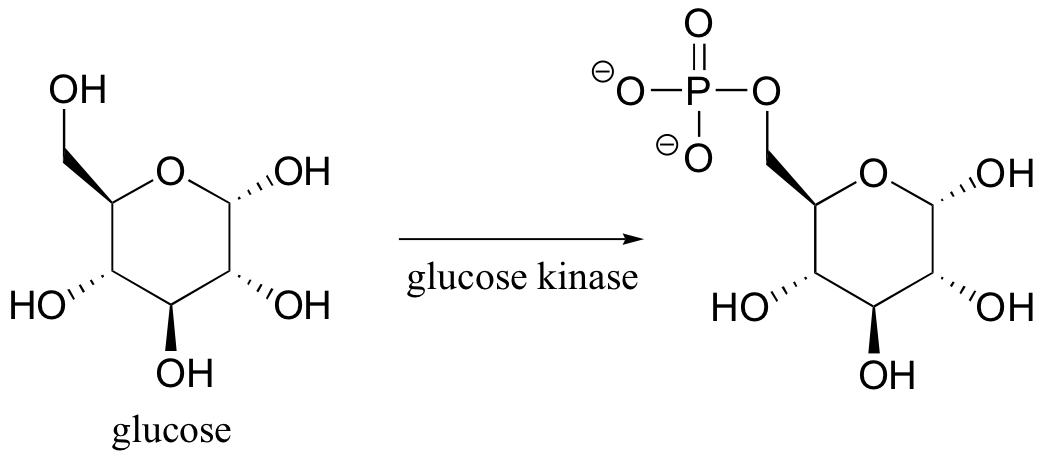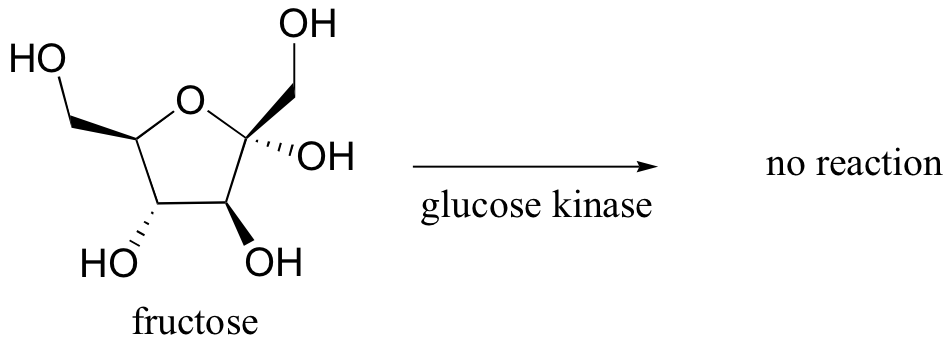An enzyme that attaches a phosphate group to glucose, for example, will not do anything at all to fructose.Glucose kinase is able to find and recognize glucose out of all of the other molecules floating around in the ‘chemical soup’ of a cell. A different enzyme, fructokinase, specifically catalyzes the phosphorylation of fructose.We have already learned that enzymes are very specific in terms of the stereochemistry of the reactions that they catalyze . Enzymes are also highly regiospecific, acting at only one specific part of a molecule. Notice that in the glucose kinase reaction above only one of the alcohol groups is phosphorylated.Finally, enzymes are capable of truly amazing rate acceleration.  Typical enzymes will speed up a reaction by anywhere from a million to a billion times, and  the most efficient enzyme currently known to scientists is believed to accelerate its reaction by a factor of about 10¹⁷ (see Chemical and Engineering News, March 13, 2000, p. 42 for an interesting discussion about this enzyme, orotidine monophosphate decarboxylase).We will now begin an exploration of some of the basic ideas about how enzymes accomplish these amazing feats of catalysis, and these ideas will be revisited often throughout the rest of the text as we consider various examples of enzyme-catalyzed organic reactions.  But in order to begin to understand how enzymes work, we will first need to learn (or review, as the case may be) a little bit about protein structure.

CC licensed content, Shared previously

• 6.3: Enzymatic catalysis - the basic ideas. Authored by: Tim Soderbergu00a0(University of Minnesota, Morris). Located at: https://chem.libretexts.org/Textbook_Maps/Organic_Chemistry/Book%3A_Organic_Chemistry_with_a_Biological_Emphasis_(Soderberg)/Chapter_06%3A_Introduction_to_organic_reactivity_and_catalysis/6.3%3A_Enzymatic_catalysis_-_the_basic_ideas. Project: Chemistry LibreTexts. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike