5.2: Thermodynamics of reactions
- Page ID
- 225785
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Fundamentals
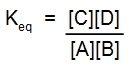
- ΔGo = 0, Keq = 1, the reaction is equally balanced.
- ΔGo is negative, Keq > 1, the reaction favors the products
- ΔGo is positive, Keq < 1, the reaction favors the reactants
Free energy relates to the heat change through the equation (ΔH)
This tells us that a more negative ΔH (exothermic reaction) will help favor the products. Also, a positive entropy change (increase in disorder) will also help form the products, especially at higher temperatures.
Bond dissociation energy
Introduction
Breaking a covalent bond between two partners, A-B, can occur either heterolytically, where the shared pair of electron goes with one partner or another
\[A-B \rightarrow A^+ + B:^-\]
or
\[A-B \rightarrow A:^- + B^+ \]
or homolytically, where one electron stays with each partner.
\[A-B \rightarrow A^• + B^• \]
The products of homolytic cleavage are radicals and the energy that is required to break the bond homolytically is called the Bond Dissociation Energy (BDE) and is a measure of the strength of the bond.
Calculation of the BDE
The BDE for a molecule A-B is calculated as the difference in the enthalpies of formation of the products and reactants for homolysis.
Officially, the IUPAC definition of bond dissociation energy refers to the energy change that occurs at 0 K, and the symbol is $$D_o$$. However, it is commonly referred to as BDE, the bond dissociation energy, and it is generally used, albeit imprecisely, interchangeably with the bond dissociation enthalpy, which generally refers to the enthalpy change at room temperature (298K). Although there are technically differences between BDEs at 0 K and 298 K, those difference are not large and generally do not affect interpretations of chemical processes.
Bond breakage/formation
Bond dissociation energy (or enthalpy) is a state function and consequently does not depend on the path by which it occurs. Therefore, the specific mechanism in how a bond breaks or is formed does not affect the BDE. Bond dissociation energies are useful in assessing the energetics of chemical processes. For chemical reactions, combining bond dissociation energies for bonds formed and bonds broken in a chemical reaction using Hess’s Law can be used to estimate reaction enthalpies.
Example: Chlorination of Methane
Consider the chlorination of methane
CH4 + Cl2 → CH3Cl + HCl
The overall reaction thermochemistry can be calculated exactly by combining the BDEs for the bonds broken and bonds formed, i.e., ΔH = BDE(bonds broken) – BDE(bonds made)
The “bonds made” part of the equation is negative because it represents the opposite of bonds broken, the BDE.
CH4 → CH3• + H• BDE(CH3-H)
Cl2 → 2Cl• BDE(Cl-Cl)
H• + Cl• → HCl -BDE(H-Cl)
CH3• + Cl• → CH3Cl -BDE(CH3-Cl)
—————————————————
CH4 + Cl2 → CH3Cl + HCl
ΔH = BDE(CH3−H) + BDE(Cl-Cl) − BDE(H-Cl) − BDE(CH3−Cl)
Because reaction enthalpy is a state function, it does not matter what reactions are combined to make up the overall process using Hess’s Law. However, BDEs are convenient to use because they are readily available.
Alternatively, BDEs can be used to assess individual steps of a mechanism. For example, an important step in free radical chlorination of alkanes is the abstraction of hydrogen from the alkane to form a free radical.
RH + Cl• → R• + HCl
The energy change for this step is equal to the difference in the BDEs in RH and HCl
\[\Delta H = BDE(R-H) – BDE(HCl)\]
This relationship shows that the hydrogen abstraction step is more favorable when BDE(R-H) is smaller. The difference in energies accounts for the selectivity in the halogenation of hydrocarbons with different types of C-H bonds.
Representative C-H BDEs in Organic Molecules
| R-H | Do, kJ/mol | D298, kJ/mol | R-H | Do, kJ/mol | D298, kJ/mol |
| CH3-H | 432.7±0.1 | 439.3±0.4 | H2C=CH-H | 456.7±2.7 | 463.2±2.9 |
| CH3CH2-H | 423.0±1.7 | C6H5-H | 465.8±1.9 | 472.4±2.5 | |
| (CH3)2CH-H | 412.5±1.7 | HCCH | 551.2±0.1 | 557.8±0.3 | |
| (CH3)3C-H | 403.8±1.7 | ||||
| H2C=CHCH2-H | 371.5±1.7 | ||||
| HC(O)-H | 368.6±0.8 | C6H5CH2-H | 375.3±2.5 | ||
| CH3C(O)-H | 374.0±1.2 |


