4.1: Chirality

Introduction

Begin this chapter by watching this video, which gives an overview of the main topics:

A Vimeo element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/ochem1walker/?p=65

Stereoisomers are isomers that differ in the spatial arrangement of atoms, rather than the order of atomic connectivity. One of the most interesting types of isomer is mirror-image stereoisomers, a non-superimposable set of two molecules that are mirror images of one another. The existence of these molecules is determined by concept known as chirality. The word “chiral” was derived from the Greek word for hand, because our hands are good example of chirality since they are non-superimposable mirror images of each other.

We turn now to concept of chirality, discovered and explored by Louis Pasteur .  The term chiral, from the Greek work for ‘hand’,  refers to anything which cannot be superimposed on its own mirror image.  Your hands, of course, are chiral – you cannot superimpose your left hand on your right, and you cannot fit your left hand into a right-handed glove (which is also a chiral object). Another way of saying this is that your hands do not have a mirror plane of symmetry: you cannot find any plane which bisects your hand in such a way that one side of the plane is a mirror image of the other side. Chiral objects do not have a plane of symmetry.

Your face, on the other hand is achiral – lacking chirality – because, some small deviations notwithstanding, you could superimpose your face onto its mirror image.  If someone were to show you a mirror image photograph of your face, you could line the image up, point-for-point, with your actual face. Your face has a plane of symmetry, because the left side is the mirror image of the right side.

What Pasteur, Biot, and their contemporaries did not yet fully understand when Pasteur made his discovery of molecular chirality was the source of chirality at the molecular level.  It stood to reason that a chiral molecule is one that does not contain a plane of symmetry, and thus cannot be superimposed on its mirror image.  We now know that chiral molecules contain one or more chiral centers, which are almost always tetrahedral (sp³-hybridized) carbons with four different substituents. Consider the cartoon molecule A below: a tetrahedral carbon, with four different substituents denoted by balls of  four different colors (for the time being, don’t worry about exactly what these substituents could be – we will see real examples very soon).

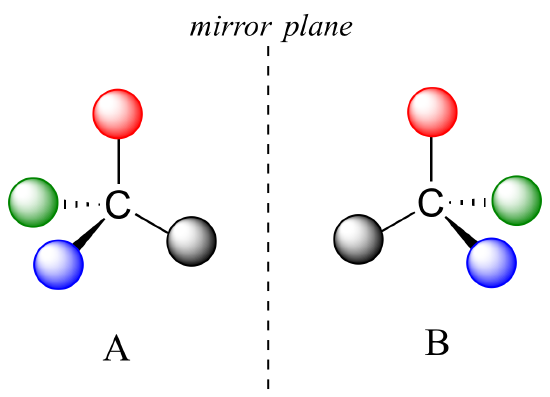
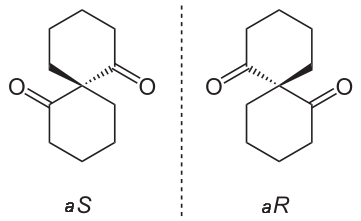
The mirror image of A, which we will call B, is drawn on the right side of the figure, and an imaginary mirror is in the middle.  Notice that every point on A lines up through the mirror with the same point on B: in other words, if A looked in the mirror, it would see B looking back.

Now, if we flip compound A over and try to superimpose it point for point on compound B, we find that we cannot do it: if we superimpose any two colored balls, then the other two are misaligned.

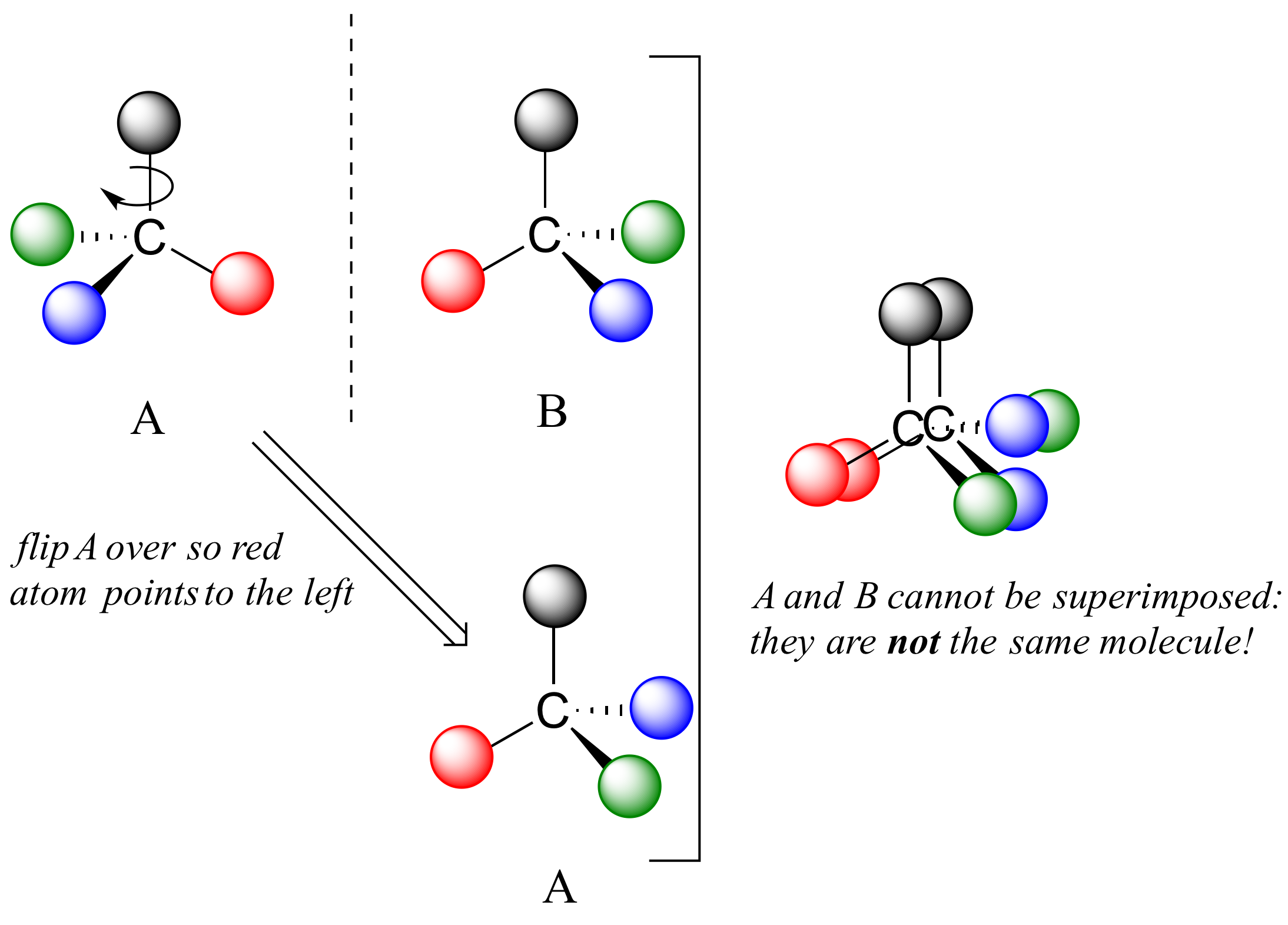
A is not superimposable on its mirror image (B), thus by definition A is a chiral molecule.  It follows that B also is not superimposable on its mirror image (A), and thus it is also a chiral molecule.  Also notice in the figure below (and convince yourself with models) that neither A nor B has an internal plane of symmetry.

A and B are stereoisomers: molecules with the same molecular formula and the same bonding arrangement, but a different arrangement of atoms in space.  There are two types of stereoisomers: enantiomers and diastereomers.  Enantiomers are pairs of stereoisomers which are mirror images of each other: thus, A and B are enantiomers.  It should be self-evident that a chiral molecule will always have one (and only one) enantiomer: enantiomers come in pairs. Enantiomers have identical physical properties (melting point, boiling point, density, and so on).  However, enantiomers do differ in how they interact with polarized light (we will learn more about this soon) and they may also interact in very different ways with other chiral molecules – proteins, for example.

Diastereomers are stereoisomers which are not mirror images of each other. For now, we will concentrate on understanding enantiomers, and come back to diastereomers later.

We defined a chiral center as a tetrahedral carbon with four different substituents.  If, instead, a tetrahedral carbon has two identical substituents (two black atoms in the cartoon figure below), then of course it still has a mirror image (everything has a mirror image, unless we are talking about a vampire!) However, it is superimposable on its mirror image, and has a plane of symmetry.

This molecule is achiral (lacking chirality). Using the same reasoning, we can see that a trigonal planar (sp²-hybridized) carbon is also not a chiral center.

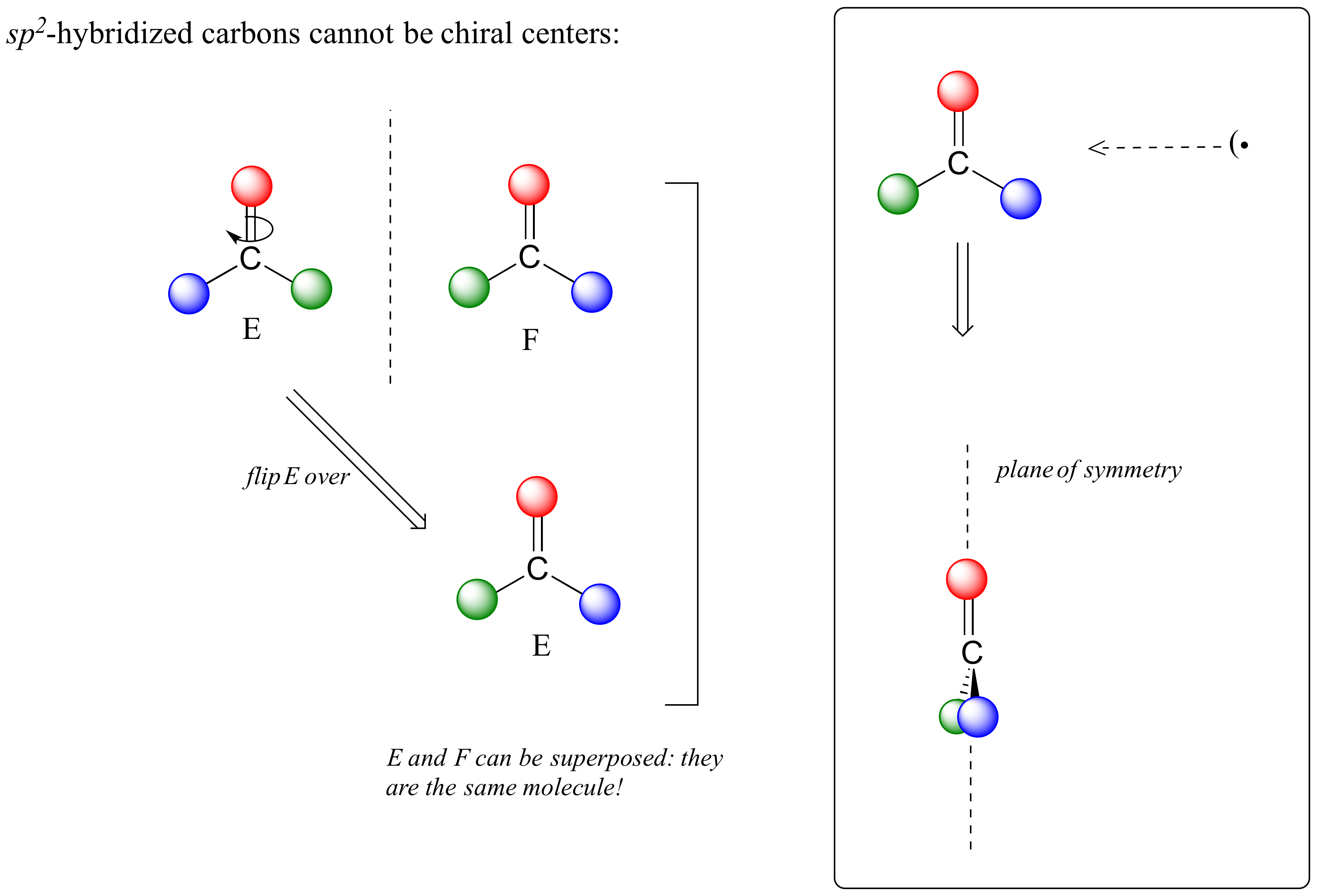
Notice that structure E can be superimposed on F, its mirror image – all you have to do is pick E up, flip it over, and it is the same as F.  This molecule has a plane of symmetry, and is achiral.

Let’s apply our general discussion to real molecules.  For now, we will limit our discussion to molecules with a single chiral center.  It turns out that tartaric acid, the subject of our chapter introduction, has two chiral centers, so we will come back to it later.

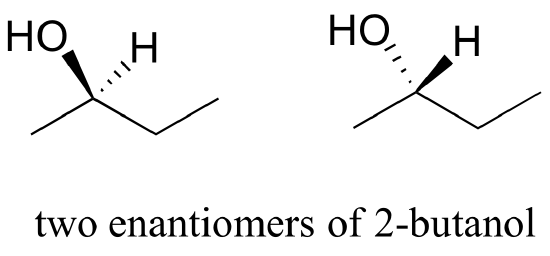
Consider 2-butanol, drawn in two dimensions below.

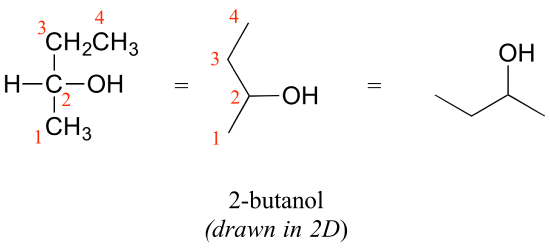
Carbon #2 is a chiral center: it is sp³-hybridized and tetrahedral (even though it is not drawn that way above), and the four things attached to is are different: a hydrogen, a methyl (-CH₃) group, an ethyl (-CH₂CH₃) group, and a hydroxyl (OH) group.  Let’s draw the bonding at C₂ in three dimensions, and call this structure A.  We will also draw the mirror image of A, and call this structure B.

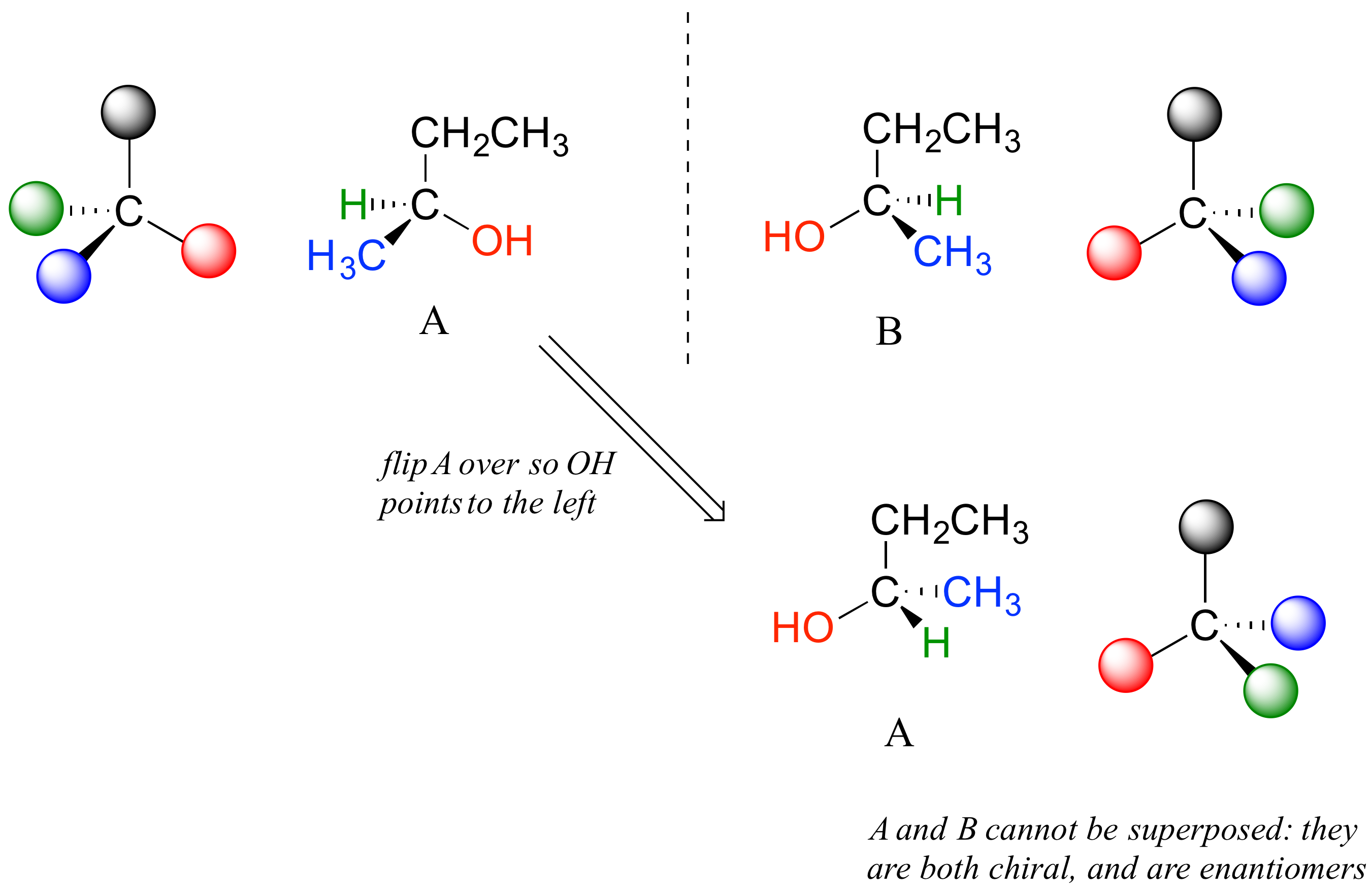
When we try to superimpose A onto B, we find that we cannot do it.  A and B are both chiral molecules, and they are enantiomers of each other.

2-propanol, unlike 2-butanol, is not a chiral molecule.  Carbon #2 is bonded to two identical substituents (methyl groups), and so it is not a chiral center.

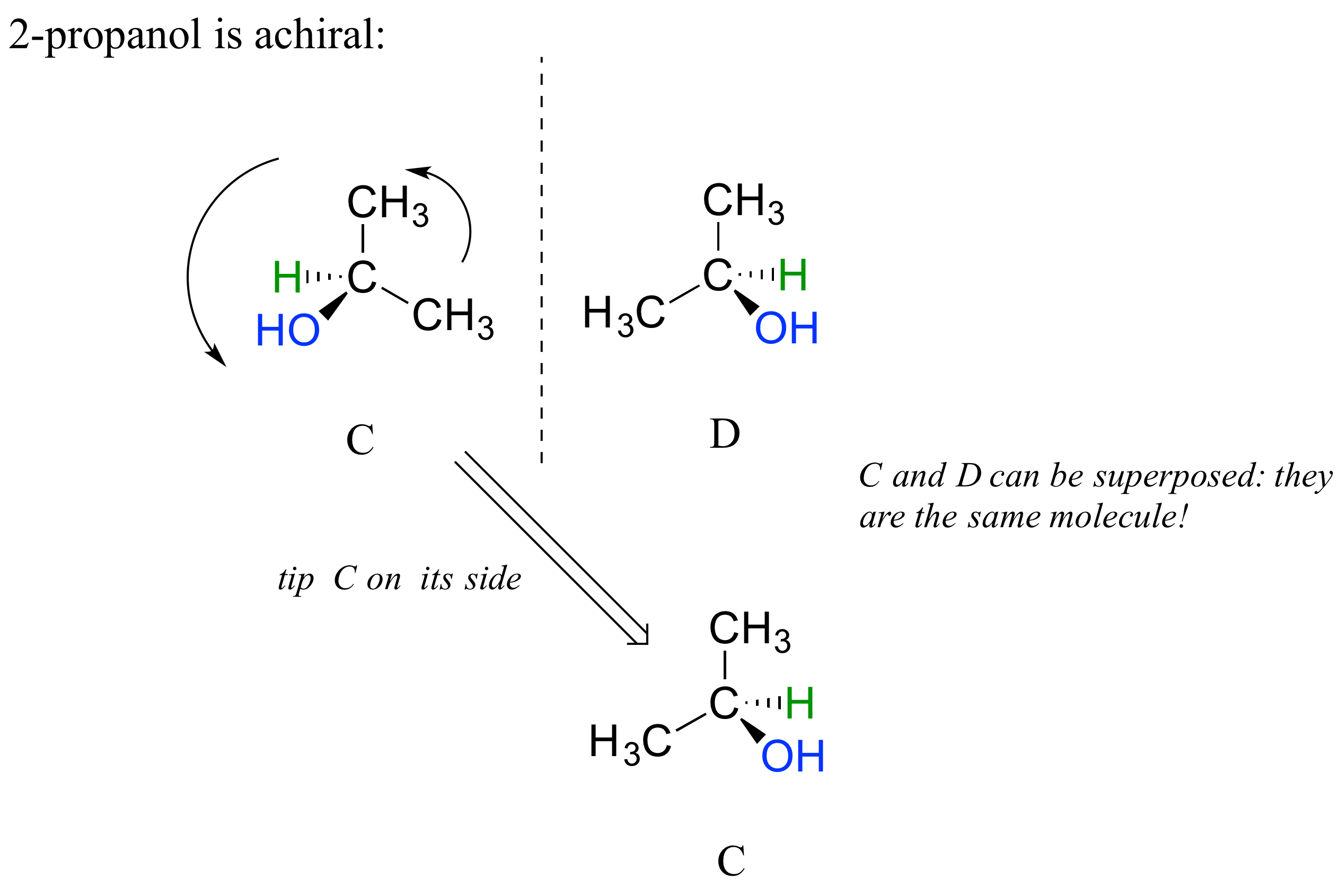
Notice that 2-propanol is superimposable on its own mirror image.

When we look at very simple molecules like 2-butanol, it is not difficult to draw out the mirror image and recognize that it is not superimposable.  However, with larger, more complex molecules, this can be a daunting challenge in terms of drawing and three-dimensional visualization.  The easy way to determine if a molecule is chiral is simply to look for the presence of one or more chiral centers: molecules with chiral centers will (almost always) be chiral.  We insert the ‘almost always’ caveat here because it is possible to come up with the exception to this rule.

Here’s another trick to make your stereochemical life easier: if you want to draw the enantiomer of a chiral molecule, it is not necessary to go to the trouble of drawing the point-for-point mirror image, as we have done up to now for purposes of illustration.  Instead, keep the carbon skeleton the same, and simply reverse the solid and dashed wedge bonds on the chiral carbon: that accomplishes the same thing.  You should use models to convince yourself that this is true, and also to convince yourself that swapping any two substituents about the chiral carbon will result in the formation of the enantiomer.

Here are four more examples of chiral biomolecules, each one shown as a pair of enantiomers, with chiral centers marked by red dots.

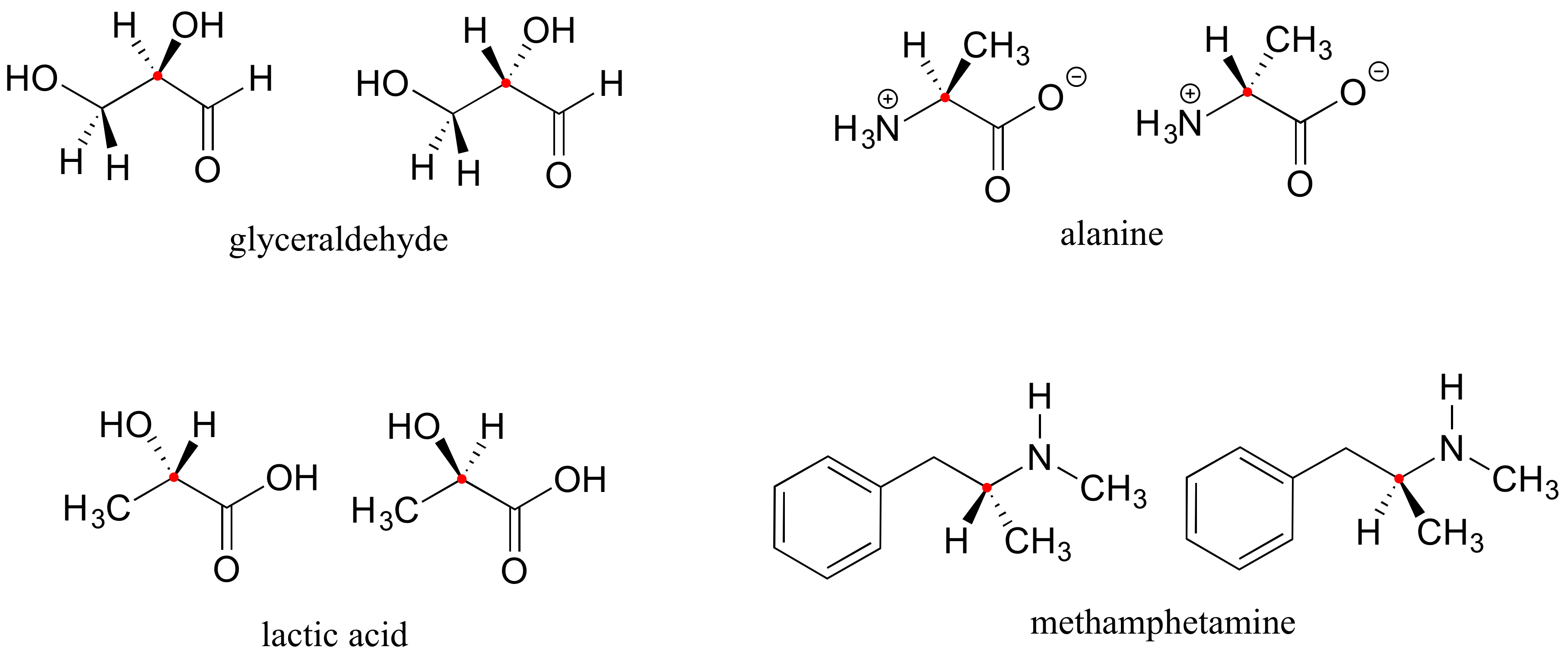
Here are some examples of achiral biomolecules – convince yourself that none of them contain a chiral center:

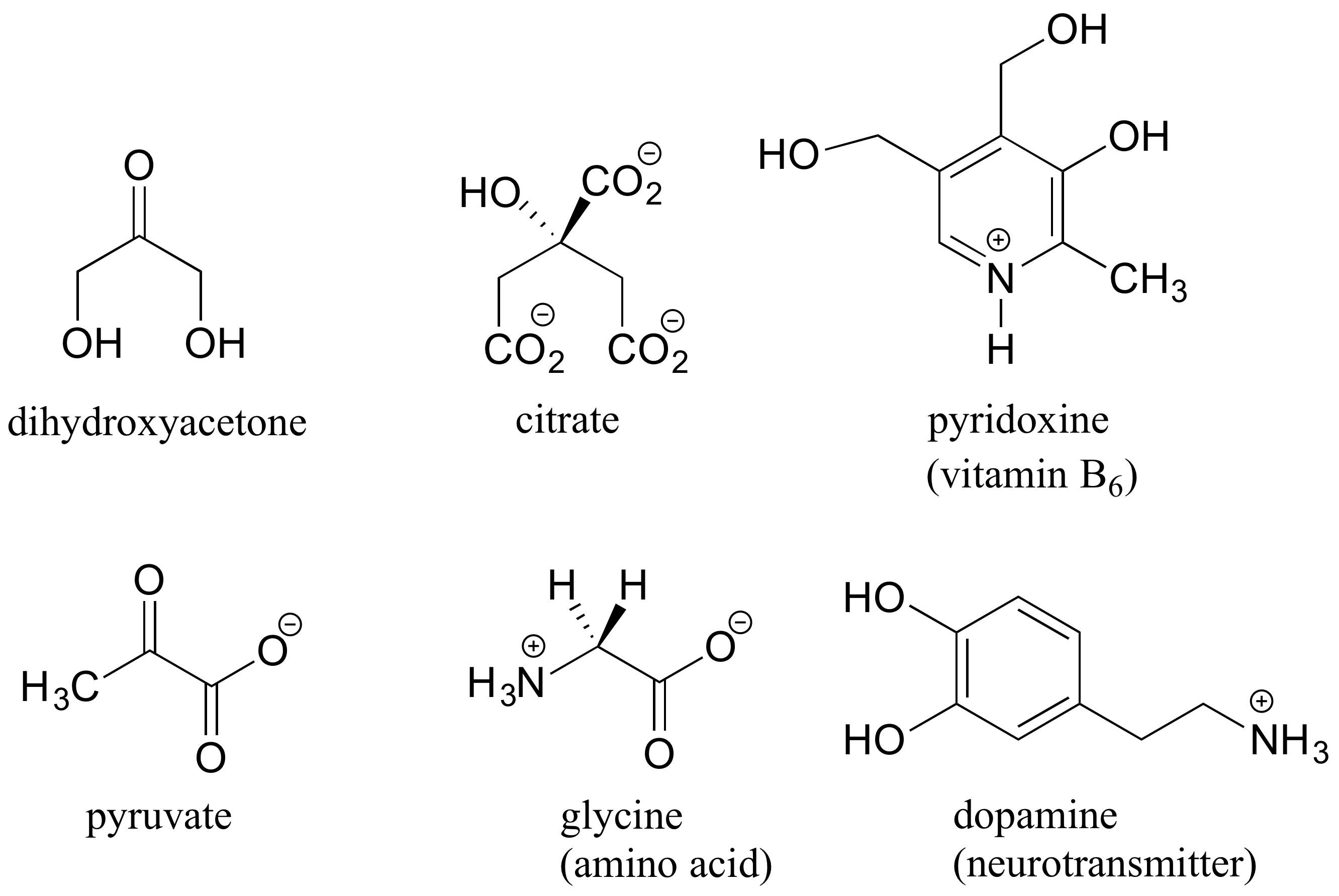
When looking for chiral centers, it is important to recognize that the question of whether or not the dashed/solid wedge drawing convention is used is irrelevant.  Chiral molecules are sometimes drawn without using wedges (although obviously this means that stereochemical information is being omitted). Conversely, wedges may be used on carbons that are not chiral centers – look, for example, at the drawings of glycine and citrate in the figure above.

Can a chiral center be something other than a tetrahedral carbon with four different substituents?  The answer to this question is ‘yes’ – however, these alternative chiral centers are less common, and outside the scope of our discussion here.

You may also have wondered about amines: shouldn’t we consider a secondary or tertiary amine to be a chiral center, as they are tetrahedral and attached to four different substituents, if the lone-pair electrons are counted as a ‘substituent’? Put another way, isn’t an amine non-superimposable on its mirror image?

The answer: yes it is, in the static picture, but in reality, the nitrogen of an amine is rapidly and reversibly inverting, or turning inside out, at room temperature.

If you have trouble picturing this, take an old tennis ball and cut it in half.   Then, take one of the concave halves and flip it inside out, then back again: this is what the amine is doing. The end result is that the two ‘enantiomers’ if the amine are actually two rapidly interconverting forms of the same molecule, and thus the amine itself is not a chiral center.  This inversion process does not take place on a tetrahedral carbon, which of course has no lone-pair electrons.

When we go to the third row in the periodic table, with elements such as sulfur and phosphorus, this process of flipping the lone pairs is much slower, so we can resolve enantiomers for compounds such as phosphines (the phosphorus analog of amines).

Exercises

1. Locate all of the chiral centers (there may be more than one in a molecule). Remember, hydrogen atoms bonded to carbon usually are not drawn in the line structure convention – but they are still there!

[reveal-answer q=”747696″]Show Solution[/reveal-answer]
[hidden-answer a=”747696″]

Chiral centers are designated with a dot.

[/hidden-answer]

2.

a) Draw two enantiomers of i) mevalonate and ii) serine.

b) Are the two 2-butanol structures below enantiomers?

[reveal-answer q=”792205″]Show Solution[/reveal-answer]
[hidden-answer a=”792205″]

(there are other ways that the two enantiomers can be drawn correctly – check your drawing with your instructor or tutor)

a)

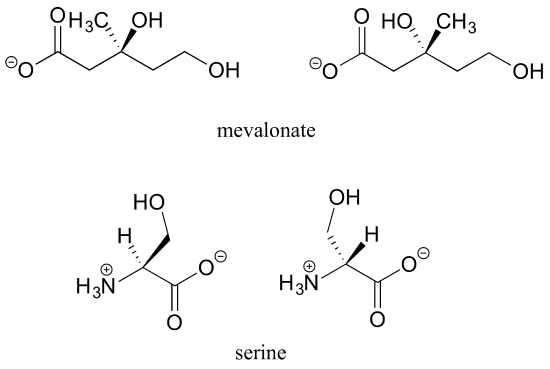
b) No, the two structures are identical.  In both drawings, the bond to the OH is pointing out of the plane of the page – it doesn’t matter whether the solid wedge is pointing to the left or the right. Make models of the two drawings and you will see they are exactly the same.

[/hidden-answer]

3. Label the molecules below as chiral or achiral, and locate all chiral centers.

 

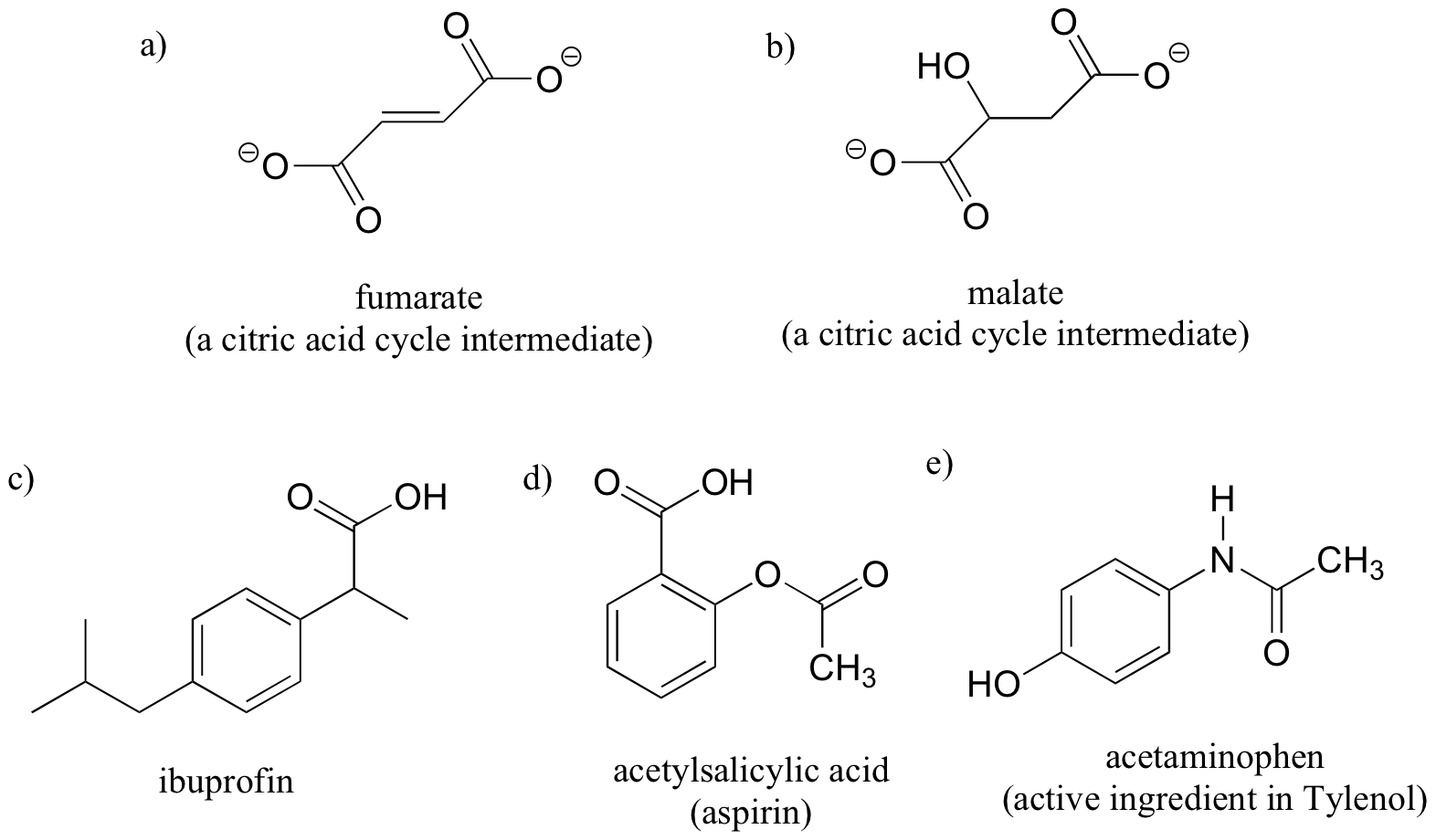
[reveal-answer q=”353104″]Show Solution[/reveal-answer]
[hidden-answer a=”353104″][/hidden-answer]

Khan Academy video tutorials

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/ochem1walker/?p=65

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/ochem1walker/?p=65

Fundamentals of Chirality

Stereoisomers are isomers that differ in spatial arrangement of atoms, rather than order of atomic connectivity. One of their most interesting type of isomer is the mirror-image stereoisomers, a non-superimposable set of two molecules that are mirror image of one another. The existance of these molecules are determined by concept known as chirality. The word “chiral” was derived from the Greek word for hand, because our hands display a good example of chirality since they are non-superimposable mirror images of each other.

Introduction

The opposite of chiral is achiral. Achiral objects are superimposable with their mirror images. For example, two pieces of paper are achiral. In contrast, chiral molecules, like our hands, are non superimposable mirror images of each other.

Try to line up your left hand perfectly with your right hand, so that the palms are both facing in the same directions. Spend about a minute doing this. Do you see that they cannot line up exactly?   The same thing applies to some molecules.

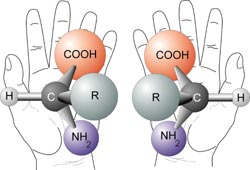
A chiral molecule has a mirror image that cannot line up with it perfectly- the mirror images are non superimposable. The mirror images are called enantiomers.

But why are chiral molecules so interesting? A chiral molecule and its enantiomer have the same chemical and physical properties(boiling point, melting point,polarity, density etc…). It turns out that many of our biological molecules such as our DNA, amino acids and sugars, are chiral molecules.

It is pretty interesting that our hands seem to serve the same purpose but most people are only able to use one of their hands to write. Similarily this is true with chiral biological molecules and interactions. Just like your left hand will not fit properly in your right glove, one of the enantiomers of a molecule may not work the same way in your body.  This must mean that enantiomers have properties that make them unique to their mirror images. One of these properties is that they cannot have a plane ofsymmetry or an internal mirror plane. So, a chiral molecule cannot be divided in two mirror image halves. Another property of chiral molecules is optical activity.

Properties of Enantiomers

A very important point to keep in mind about any pair of enantiomers is that they will have identical chemical and physical properties, except for the signs of their optical rotations, with one important proviso: All of the properties to be compared must be determined using achiral reagents in a solvent made up of achiral molecules or, in short, in an achiral environment. Thus the melting and boiling points (but not the optical rotations) of $$5$$ and $$6$$ will be identical in an achiral environment.

As mentioned before, chiral molecules are very similar to each other since they have the same components to them. The only thing that obviously differs is their arrangement in space. As a result of this similarity, it is very hard to distinguish chiral molecules from each other when we try to compare their properties such as boiling points, melting points and densities.

However, we can differentiate them by their optical activity.

Optical Activity

Chiral molecules, as we learned in the introduction to this chapter, have an interesting optical property. You may know from studying physics that light waves are oscillating electric and magnetic fields.  In ordinary light, the oscillation is randomly oriented in an infinite number of planes. When ordinary light is passed through a polarizer, all planes of oscillation are filtered out except one, resulting in plane-polarized light.

A beam of plane-polarized light, when passed through a sample of a chiral compound, interacts with the compound in such a way that the angle of oscillation will rotate. This property is called optical activity.

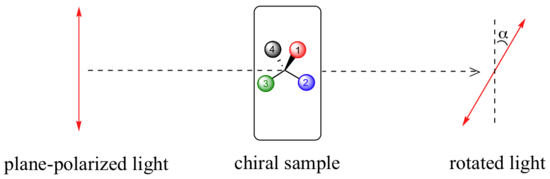
If a compound rotates plane polarized light in the clockwise (+) direction, it is said to be dextrorotatory, while if it rotates light in the counterclockwise (-) direction it is levorotatory.  The magnitude of the observed optical activity is dependent on temperature, the wavelength of light used, solvent, concentration of the chiral sample, and the path length of the sample tube  (path length is the length that the plane-polarized light travels through the chiral sample).  Typically, optical activity measurements are made in a 1 decimeter (10 cm) path-length sample tube at 25 °C, using as a light source the so-called “D-line” from a sodium lamp, which has a wavelength of 589 nm.  The specific rotation of a pure chiral compound at 25° is expressed by the expression:

. . . where alpha_(obs) is the observed rotation, l  is path length in decimeters, and c is the concentration of the sample in grams per 100 mL.  In other words, the specific rotation of a chiral compound is the optical rotation that is observed when 1 g of the compound is dissolved in enough of a given solvent to make 100 mL solution, and the rotation is measured in a 1 dm cuvette at 25 ^oC using light from a sodium lamp.

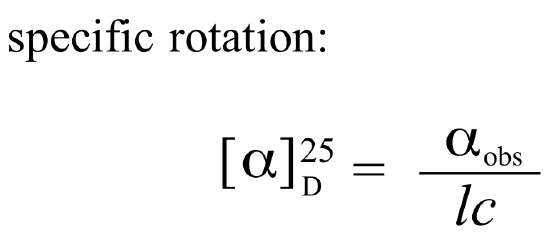
Every chiral molecule has a characteristic specific rotation, which is recorded in the chemical literature as a physical property just like melting point or density.  Different enantiomers of a compound will always rotate plane-polarized light with an equal but opposite magnitude. (S)-ibuprofen, for example, has a specific rotation of +54.5^o (dextrorotatory) in methanol, while (R)-ibuprofen has a specific rotation of -54.5^o.  There is no relationship between chiral compound’s R/S designation and the direction of its specific rotation.   For example, the S enantiomer of ibuprofen is dextrorotatory, but the S enantiomer of glyceraldehyde is levorotatory.  A 50:50 mixture of two enantiomers (a racemic mixture)  will have no observable optical activity, because the two optical activities cancel each other out.

Chiral molecules are often labeled according to whether they are dextrorotatory or levorotatory (their effect on light) as well as by their R/S designation (their absolute structure in 3D).  For example, the pure enantiomers of ibuprofen are labeled (S)-(+)-ibuprofen and (R)-(-)-ibuprofen, while (±)-ibuprofen refers to the racemic mixture, which is the form in which the drug is sold to consumers.

It is very important to know that d, l, ($$+$$), or ($$-$$) do not designate configurations. Thus, although ($$+$$)-2-butanol actually has configuration $$5$$ and ($$-$$)-2-butanol has configuration $$6$$, there is no simple way to predict that a particular sign of rotation will be associated with a particular configuration. Methods used in assigning the true configurations to enantiomers will be discussed later.

Schematic representation of the rotation of the plane of polarization of polarized light by an optically active compound. Plane-polarized light is different from ordinary light in that its electrical component vibrates in a plane rather than in all directions. The angle $\alpha$ is the angle between the plane of polarization of light entering the sample and the plane of polarization of the emerging light.

History of enantiomers and optical activity

It was discovered early in the nineteenth century that many compounds, whether solid, liquid, or gas, have the property of rotating the plane of polarization of polarized light and can be said to be “optically active.” A satisfactory explanation of the origin of optical activity came much later and developed in its modern form from the classic researches of Louis Pasteur, and from the concept of the three-dimensional carbon atoms expressed independently by J. H. van’t Hoff and J. A. Le Bel.$$^2$$

Pasteur’s contribution to stereochemistry came as a result of his studies of the shapes of crystals of tartaric acid, $$HO_2C-CHOH-CHOH-CO_2H$$, and its salts. Tartaric acid, a by-product of wine production, was known to be optically active, and Pasteur showed that it, and nineteen different salts of it, all formed crystals that were not identical with their mirror images. A different substance known as “racemic acid,” for which we can write the same condensed formula, $$HO_2C-CHOH-CHOH-CO_2H$$, was known to be optically inactive, and Pasteur expected that when he crystallized this acid or its salts he would obtain crystals that would be identical with their mirror images. However, crystallization of the sodium ammonium salt of racemic acid from water at temperatures below $$28^\text{o}$$ gave crystals of two different shapes and these shapes were mirror images of one another. Pasteur carefully picked apart the two kinds of crystals and showed that one of them was identical with the corresponding salt of tartaric acid, except that it rotated the plane of polarization of polarized light in the opposite direction. This separation of racemic acid into two optically active forms now is called a “resolution of racemic acid.”

On the basis of his discoveries, Pasteur postulated that “optical isomerism” had to be related to the molecular dissymmetry of substances such that nonidentical mirror-image forms could exist. However, it remained for van’t Hoff and Le Bel to provide, almost simultaneously, a satisfactory explanation at the molecular level. In his first published work on tetrahedral carbon van’t Hoff said “…it appears more and more that the present constitutional formulae are incapable of explaining certain cases of isomerism; the reason for this is perhaps the fact that we need a more definite statement about the actual positions of the atoms.”$$^3$$ He goes on to discuss the consequences of the tetrahedral arrangements of atoms about carbon, explicitly in connection with optical isomerism and geometric, or cis-trans, isomerism.

It is not easy for the chemist of today to appreciate fully the contributions of these early chemists because we have long accepted the tetrahedral carbon as an experimentally established fact. At the time the concept was enunciated, however, even the existence of atoms and molecules was questioned openly by many scientists, and to ascribe “shapes” to what in the first place seemed like metaphysical conceptions was too much for many to accept.

Exercise

1. Which of the 20 common L-amino acids found in nature has the R configuration? Refer to the amino acid table for structures.

[reveal-answer q=”683630″]Show Solution[/reveal-answer]
[hidden-answer a=”683630″]

Cysteine is the only common L-amino acid with S configuration. This is solely due to the rules of the naming system: the carbon of the side chain – which is directly bonded to a sulfur – has higher priority than the carboxylate carbon. In the other 19 amino acids, the carboxylate carbon has priority #2, and the side chain carbon has priority #3. [/hidden-answer]

Khan Academy video tutorial on optical activity

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/ochem1walker/?p=65

Circular Dichroism

Another property of chiral molecules is called circular dichroism (CD). This pertains to their differential absorption of left and right circularly polarized light. When left and right circularly polarized light passes through chiral molecules, the absorption coefficients differ so that the change in absorption coefficients does not equal zero.

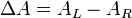
where ΔA is the difference between absorbance of left circularly polarized (LCP) and right circularly polarized (RCP) light (this is what is usually measured). Where [J] = molar concentration of the sample and l is the path length.

The CD signals of chiral molecules can give important information and this information can be used for visible and ultraviolet spectroscopy. Every chiral molecule shows a particular CD spectrum. By looking at the distinctive spectra of molecules such as proteins and DNA, we can obtain useful information about their secondary structures and see how they differ.

References

1. Atkins, Peter and de Paula, Julio. Physical Chemistry for the Life Sciences. New York, N.Y.: W. H. Freeman Company, 2006. (565-566).
2. Croft, William J. Under the Microscope: a brief history of microscopy. Singapore: Mainland Press, 2006. (39).
3. Vollhardt, K. Peter C. and Schore, Neil E. Organic Chemistry: Structure and Function. Fourth Edition. New York, N.Y.: W. H. Freeman Company, 2003. (165-169).
4. Wagniere, George H. On Chirality and the Universal Asymmetry: Reflection on Image and Mirror Image. Zurich, Switzerland, 2007. (3-7).