2.1: Combining atomic orbitals, sigma and pi bonding
- Page ID
- 225768
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Valence bond theory is most often used to describe bonding in organic molecules. In this model, bonds are considered to form from the overlap of two atomic orbitals on different atoms, each orbital containing a single electron. In looking at simple inorganic molecules such as molecular hydrogen (H2) or hydrogen fluoride (HF), our present understanding of s and p atomic orbitals will suffice. In order to explain the bonding in organic molecules, however, we will need to introduce the concept of hybrid orbitals (see section 2.2.).
The sigma bond in the H2 molecule
The simplest case to consider is the hydrogen molecule, H2. When we say that the two hydrogen nuclei share their electrons to form a covalent bond, what we mean in valence bond theory terms is that the two spherical 1s orbitals (the grey spheres in the figure below) overlap, and contain two electrons with opposite spin.
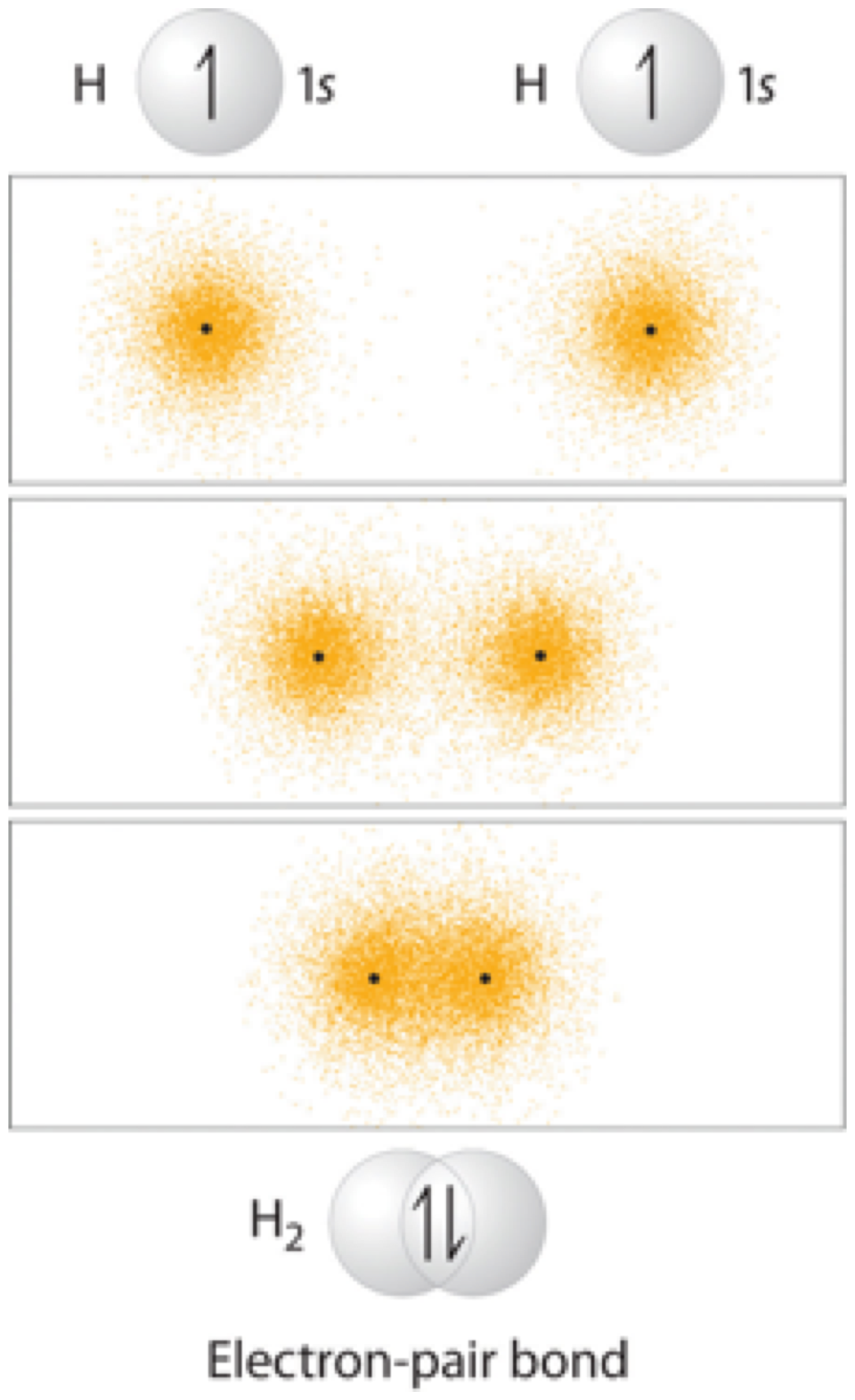
These two electrons are now attracted to the positive charge of both of the hydrogen nuclei, with the result that they serve as a sort of ‘chemical glue’ holding the two nuclei together.
How far apart are the two nuclei? If they are too far apart, their respective 1s orbitals cannot overlap, and thus no covalent bond can form – they are still just two separate hydrogen atoms. As they move closer and closer together, orbital overlap begins to occur, and a bond begins to form. This lowers the potential energy of the system, as new, attractive positive-negative electrostatic interactions become possible between the nucleus of one atom and the electron of the second.
But something else is happening at the same time: as the atoms get closer, the repulsive positive-positive interaction between the two nuclei also begins to increase.
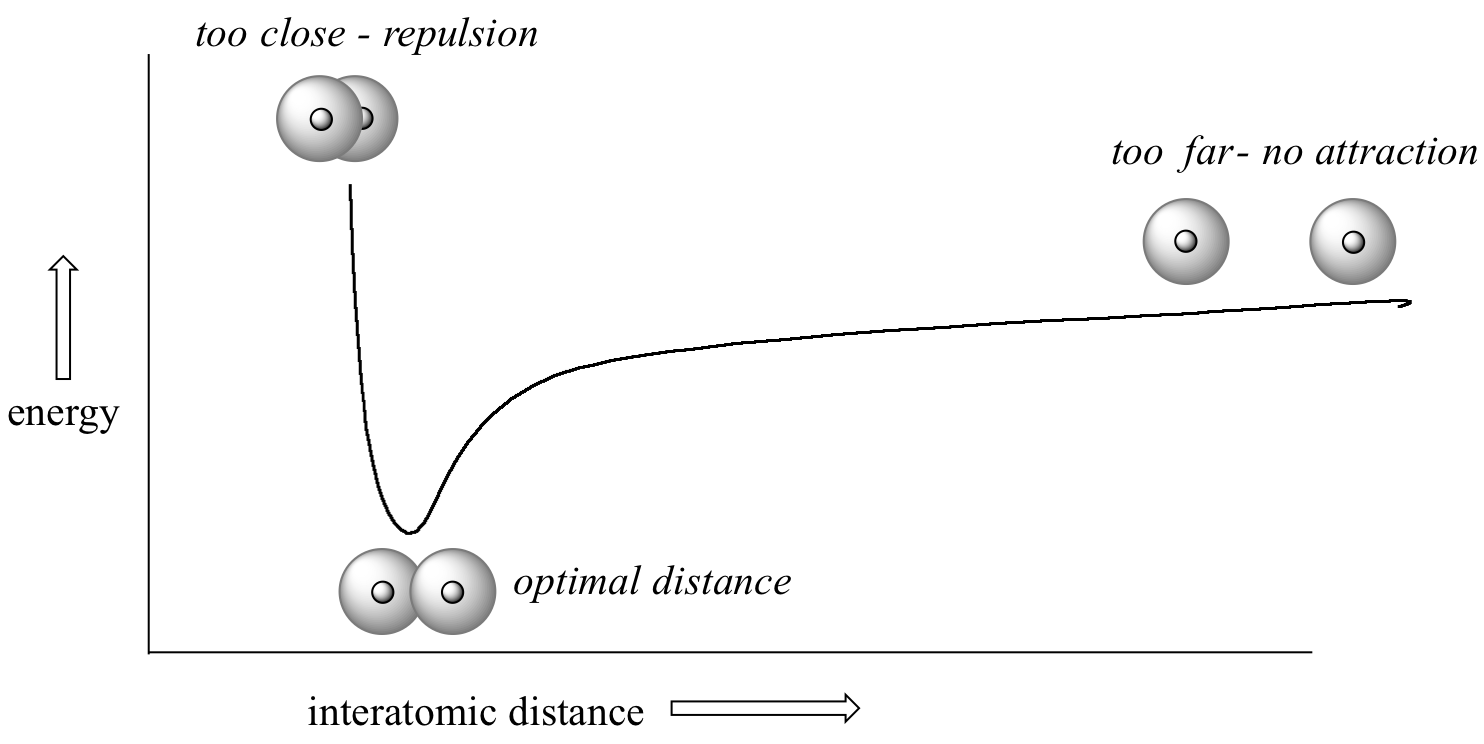
At first this repulsion is more than offset by the attraction between nuclei and electrons, but at a certain point, as the nuclei get even closer, the repulsive forces begin to overcome the attractive forces, and the potential energy of the system rises quickly. When the two nuclei are ‘too close’, we have an unstable, high-energy situation. There is a defined optimal distance between the nuclei in which the potential energy is at a minimum, meaning that the combined attractive and repulsive forces add up to the greatest overall attractive force. This optimal internuclear distance is the bond length. For the H2 molecule, the distance is 74 pm (picometers, 10-12 meters). Likewise, the difference in potential energy between the lowest energy state (at the optimal internuclear distance) and the state where the two atoms are completely separated is called the bond dissociation energy, or, more simply, bond strength. For the hydrogen molecule, the H-H bond strength is equal to about 435 kJ/mol.
Every covalent bond in a given molecule has a characteristic length and strength. In general, the length of a typical carbon-carbon single bond in an organic molecule is about 150 pm, while carbon-carbon double bonds are about 130 pm, carbon-oxygen double bonds are about 120 pm, and carbon-hydrogen bonds are in the range of 100 to 110 pm. The strength of covalent bonds in organic molecules ranges from about 234 kJ/mol for a carbon-iodine bond (in thyroid hormone, for example), about 410 kJ/mole for a typical carbon-hydrogen bond, and up to over 800 kJ/mole for a carbon-carbon triple bond.
See a table of bond lengths and bond energies
It is not accurate, however, to picture covalent bonds as rigid sticks of unchanging length – rather, it is better to picture them as springs which have a defined length when relaxed, but which can be compressed, extended, and bent. This ‘springy’ picture of covalent bonds will become very important in chapter 4, when we study the analytical technique known as infrared (IR) spectroscopy.
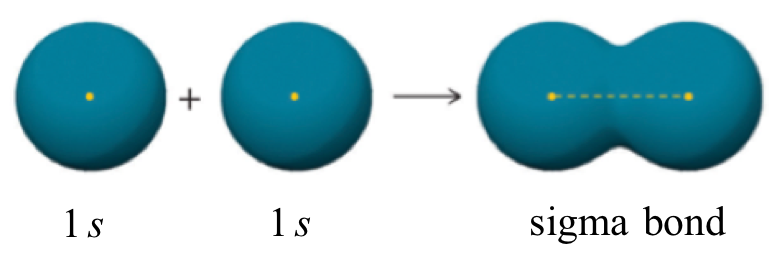
One more characteristic of the covalent bond in H2 is important to consider at this point. The two overlapping 1s orbitals can be visualized as two spherical balloons being pressed together. This means that the bond has cylindrical symmetry: if we were to take a cross-sectional plane of the bond at any point, it would form a circle. This type of bond is referred to as a σ(sigma) bond.
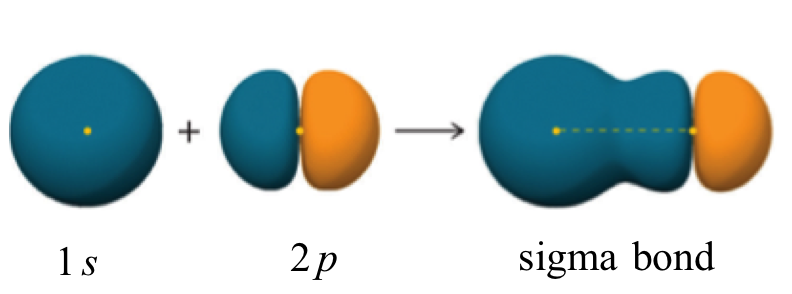
A sigma bond can be formed by overlap of an s atomic orbital with a p atomic orbital. Hydrogen fluoride (HF) is an example:
A sigma bond can also be formed by the overlap of two p orbitals. The covalent bond in molecular fluorine, F2, is a sigma bond formed by the overlap of two half-filled 2p orbitals, one from each fluorine atom.
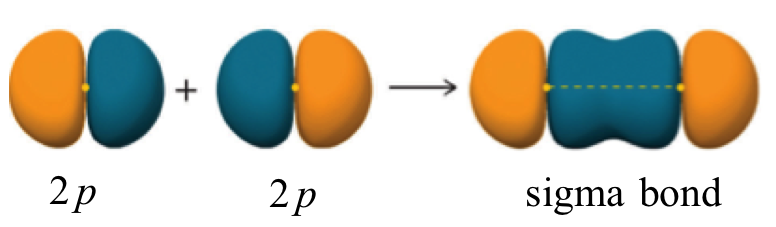
Antibonding vs. bonding Orbitals
Electrons that spend most of their time between the nuclei of two atoms are placed into the bonding orbitals, and electrons that spend most of their time outside the nuclei of two atoms are placed into antibonding orbitals. This is because there is an increasing in electron density between the nuclei in bonding orbitals, and a decreasing in electron density in antibonding orbitals (Chang 459). Placing an electron in the bonding orbital stabilizes the molecule because it is in between the two nuclei. Conversely, placing electrons into the antibonding orbitals will decrease the stability of the molecule. Electrons will fill according to the energy levels of the orbitals. They will first fill the lower energy orbitals, and then they will fill the higher energy orbitals. If a bond order of zero is obtained, that means that the molecule is too unstable and so it will not exist.
Molecular orbital theory, antibonding vs. bonding orbitals
Valence bond theory does a remarkably good job at explaining the bonding geometry of many of the functional groups in organic compounds. There are some areas, however, where the valence bond theory falls short. It fails to adequately account, for example, for some interesting properties of compounds that contain alternating double and single bonds. In order to understand these properties, we need to think about chemical bonding in a new way, using the ideas of molecular orbital (MO) theory.
Let’s go back and consider again the simplest possible covalent bond: the one in molecular hydrogen (H2). When we described the hydrogen molecule using valence bond theory, we said that the two 1s orbitals from each atom overlap, allowing the two electrons to be shared and thus forming a covalent bond. In molecular orbital theory, we make a further statement: we say that the two atomic 1s orbitals mathematically combine to form two new orbitals. Recall that an atomic orbital (such as the 1s orbital of a hydrogen atom) describes a region of space around a single atom inside which electrons are likely to be found. A molecular orbital describes a region of space around two or more atoms inside which electrons are likely to be found.
Mathematical principles tell us that when orbitals combine, the number of orbitals before the combination takes place must equal the number of new orbitals that result from the combination – orbitals don’t just disappear! We saw this previously when we discussed hybrid orbitals: one s and three p orbitals make four sp3 hybrids. When two atomic 1s orbitals combine in the formation of H2, the result is two sigma ( σ) orbitals.

Molecular orbitals for H2
According to MO theory, one sigma orbital is lower in energy than either of the two isolated atomic 1s orbitals –this lower sigma orbital is referred to as a bonding molecular orbital. The second, ‘sigma star’ (σ*) orbital is higher in energy than the two atomic 1s orbitals, and is referred to as an antibonding molecular orbital.
The bonding sigma orbital, which holds both electrons in the ground state of the molecule, is egg-shaped, encompassing the two nuclei, and with the highest likelihood of electrons being in the area between the two nuclei. The high-energy, antibonding sigma* (σ*) orbital can be visualized as a pair of droplets, with areas of higher electron density near each nucleus and a ‘node’, (area of zero electron density) midway between the two nuclei.
Remember that we are thinking here about electron behavior as wave behavior. When two separate waves combine, they can do so with constructive interference, where the two amplitudes build up and reinforce one another, or destructive interference, where the two amplitudes cancel one another out. Bonding MOs are the consequence of constructive interference between two atomic orbitals, which results in an attractive interaction and an increase in electron density between the nuclei. Antibonding MO’s are the consequence of destructive interference which results in a repulsive interaction and a region of zero electron density between the nuclei (in other words, a node).
Following the same aufbau (‘building up’) principle you learned in General Chemistry for writing out electron configurations, we place the two electrons in the H2 molecule in the lowest energy molecular orbital, which is the (bonding) sigma orbital. The bonding (attracting) MO is full, and the antibonding (repelling) MO is empty.
Double and triple bonds
Bond Order
Bond order is the number of bonds formed between two atoms. For example, three bonds are formed between a pair of nitrogen atoms, so the bond order is 3. The following is the equation to find bond order.
1/2(electrons in bonding molecular orbitals – electrons in antibonding molecular orbitals)
Bond order gives information about bond length and strength. Generally, higher bond order correlates to a shorter bond length. This is due to the greater number of bonds between the atoms. In addition, because of the greater number of bonds between the atoms, the strength should also be greater as bond order increases.
Pi (π) bonds, used to complete double and triple bonds
The first (strongest) bond to form between any two atoms (say, A and B) is a sigma bond, discussed above. To form a double or triple bond, another type of bond is needed. The Pauli Exclusion Principle (usually learnt in General Chemistry) tells us that only two electrons (= one bond) can reside in the sigma molecular orbital (σ MO) that lies directly between the two atoms (A and B). Although an antibonding orbital is available, this reduces the bond order, and putting two electrons in a σ* MO would cancel out the effect of the σ bond (and lead to “no bond”).
So in order to create a double bond (requiring four electrons in bonding orbitals), we need a different type of bonding molecular orbital. This can be achieved by combining p atomic orbitals of like sign using “side-on” overlap, as shown below.
As with σ-orbitals, combining p-orbitals in this way can either be constructive, leading to a pi (π) bonding molecular orbital, or destructive, leading to a pi star (π*) antibonding molecular orbital. This can be seen in a simple molecule with a double bond, like ethene (H2C=CH2). Each p atomic orbital contributes one electron; in the diagram, the starting energy for each electron/p atomic orbital is represented by the horizontal line on the left (for atom A) or on the right (for atom B).
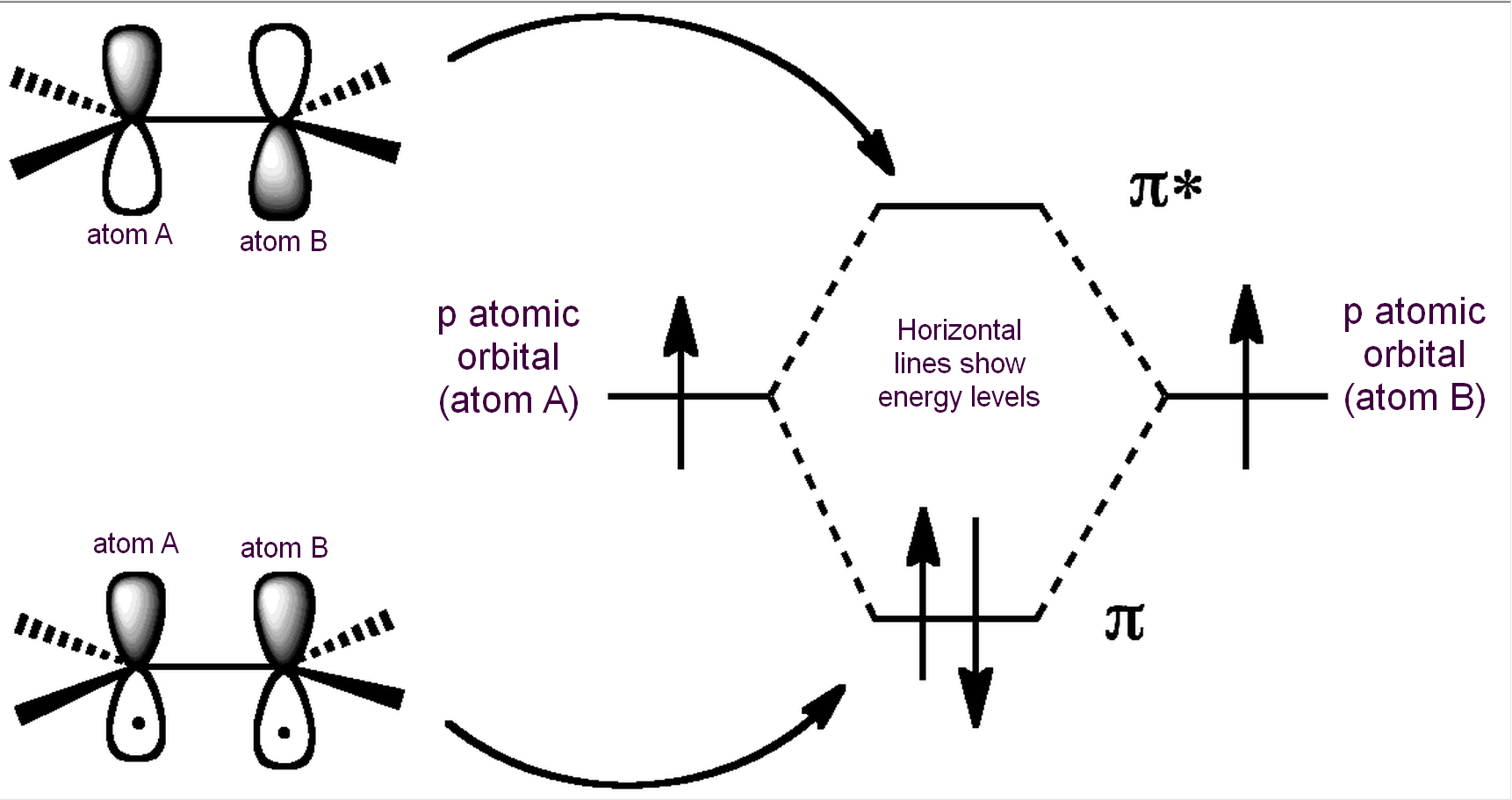
As before, the antibonding molecular orbital (π*) is higher in energy (less stable) than the bonding molecular orbital (π). This means that in the most stable energy state (the ground state), the two electrons both reside in the π-bonding MO, and the π* is empty. The shape of the final π-bonding MO is shown:

With two electrons in the sigma bonding MO, and two electrons in the pi bonding MO, and zero electrons in antibonding orbitals, we have an overall bond order of 1/2(4 – 0) = 2, i.e., a double bond.
To form a triple bond, we need to have one sigma bonding MO and two pi bonding MOs. Whereas only one sigma bonding MO is possible, the pi bonding MOs can exist either in the vertical plane or the horizontal plane, and so two pi bonds are possible. Thus we can use one sigma bond + two pi bonds to form a triple bond. Examples of this are shown and discussed in the next section.
Outside Links
References
- Chang, Raymond. Physical Chemistry for the Biosciences. University Science Books, 2005.
Further Reading
- Taken from Organic Chemistry with a Biological Emphasis. Authored by: Tim Soderberg. Provided by: University of Minnesota, Morris. Located at: https://chem.libretexts.org/Textbook_Maps/Organic_Chemistry/Book%3A_Organic_Chemistry_with_a_Biological_Emphasis_(Soderberg)/Chapter_02%3A_Introduction_to_organic_structure_and_bonding_II/2.2%3A_Molecular_orbital_theory%3A_conjugation_and_aromaticity. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike
- Diagram of bonding & antibonding pi orbitals in ethene. Authored by: User:Smokefoot. Provided by: Wikimedia Foundation. Located at: https://commons.wikimedia.org/w/index.php?curid=16625580. Project: Wikimedia Commons. License: CC BY-SA: Attribution-ShareAlike


