3.3 Conformation of Cyclohexane
- Page ID
- 17035
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Although the customary line drawings of simple cycloalkanes are geometrical polygons, the actual shape of these compounds in most cases is very different.
Cyclopropane is necessarily planar (flat), with the carbon atoms at the corners of an equilateral triangle. The 60º bond angles are much smaller than the optimum 109.5º angles of a normal tetrahedral carbon atom, and the resulting angle strain dramatically influences the chemical behavior of this cycloalkane. Cyclopropane also suffers substantial eclipsing strain, since all the carbon-carbon bonds are fully eclipsed. Cyclobutane reduces some bond-eclipsing strain by folding (the out-of-plane dihedral angle is about 25º), but the total eclipsing and angle strain remains high. Cyclopentane has very little angle strain (the angles of a pentagon are 108º), but its eclipsing strain would be large (about 10 kcal/mol) if it remained planar. Consequently, the five-membered ring adopts non-planar puckered conformations whenever possible.
Rings larger than cyclopentane would have angle strain if they were planar. However, this strain, together with the eclipsing strain inherent in a planar structure, can be relieved by puckering the ring. Cyclohexane is a good example of a carbocyclic system that virtually eliminates eclipsing and angle strain by adopting non-planar conformations. Cycloheptane and cyclooctane have greater strain than cyclohexane, in large part due to transannular crowding (steric hindrance by groups on opposite sides of the ring).
Conformations of Cyclohexane
A planar structure for cyclohexane is clearly improbable. The bond angles would necessarily be 120º, 10.5º larger than the ideal tetrahedral angle. Also, every carbon-carbon bond in such a structure would be eclipsed. The resulting angle and eclipsing strains would severely destabilize this structure. If two carbon atoms on opposite sides of the six-membered ring are lifted out of the plane of the ring, much of the angle strain can be eliminated.
This boat structure still has two eclipsed bonds and severe steric crowding of two hydrogen atoms on the "bow" and "stern" of the boat. This steric crowding is often called steric hindrance. By twisting the boat conformation, the steric hindrance can be partially relieved, but the twist-boat conformer still retains some of the strains that characterize the boat conformer. Finally, by lifting one carbon above the ring plane and the other below the plane, a relatively strain-free 'chair' conformer is formed. This is the predominant structure adopted by molecules of cyclohexane.
Investigations concerning the conformations of cyclohexane were initiated by H. Sachse (1890) and E. Mohr (1918), but it was not until 1950 that a full treatment of the manifold consequences of interconverting chair conformers and the different orientations of pendent bonds was elucidated by D. H. R. Barton (Nobel Prize 1969 together with O. Hassel). The following discussion presents some of the essential features of this conformational analysis.
On careful examination of a chair conformation of cyclohexane, we find that the twelve hydrogens are not structurally equivalent. Six of them are located about the periphery of the carbon ring, and are termed equatorial. The other six are oriented above and below the approximate plane of the ring (three in each location), and are termed axial because they are aligned parallel to the symmetry axis of the ring.
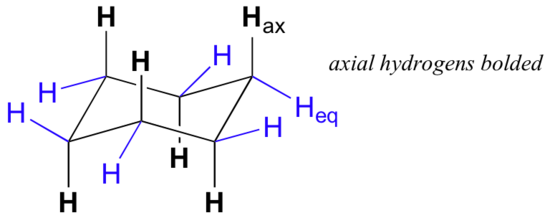
In the figure above, the equatorial hydrogens are colored blue, and the axial hydrogens are in bold. Since there are two equivalent chair conformations of cyclohexane in rapid equilibrium, all twelve hydrogens have 50% equatorial and 50% axial character. The figure below illustrates how to convert a molecular model of cyclohexane between two different chair conformations - this is something that you should practice with models. Notice that a 'ring flip' causes equatorial hydrogens to become axial, and vice-versa.
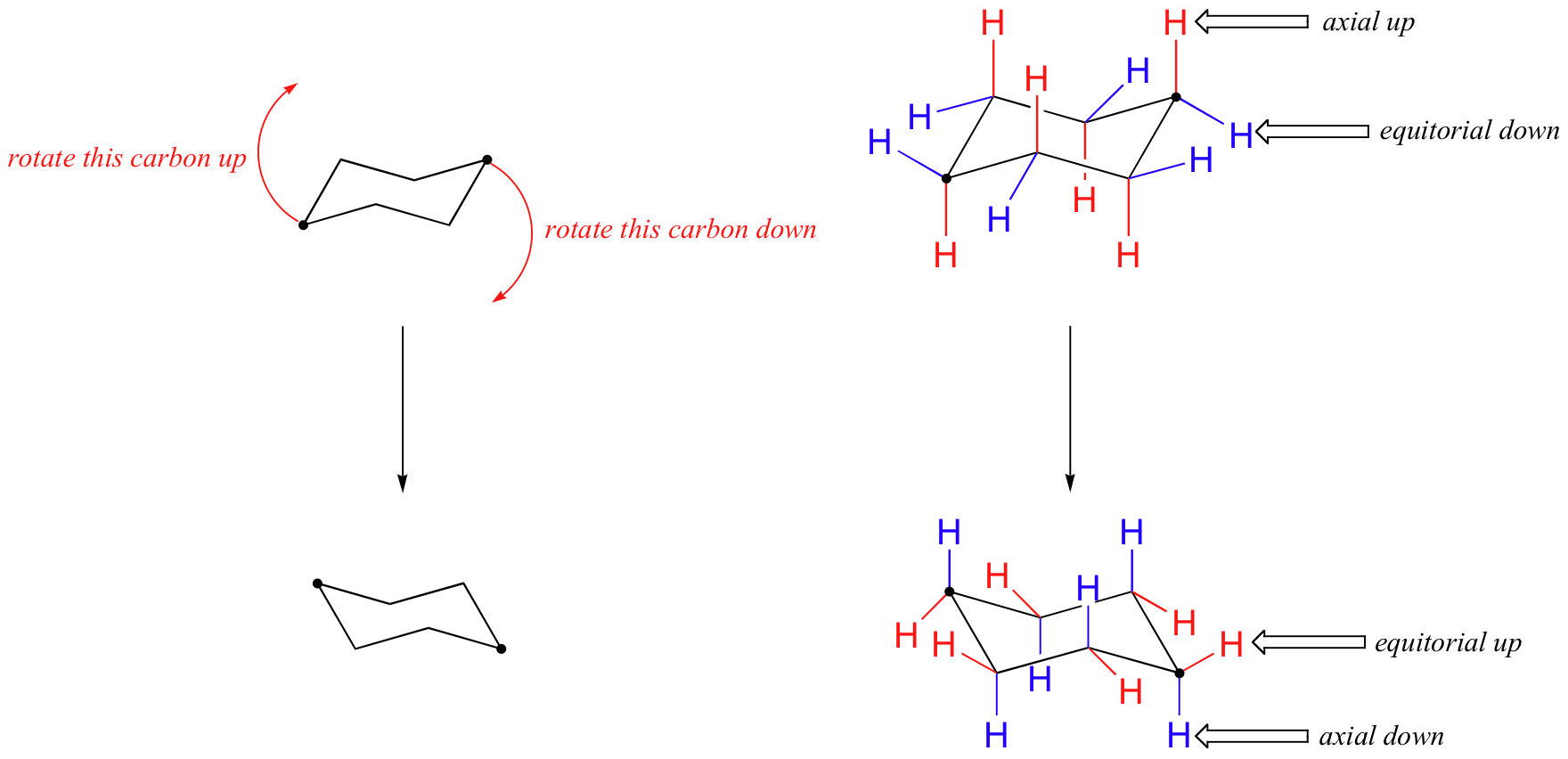
Because axial bonds are parallel to each other, substituents larger than hydrogen generally suffer greater steric crowding when they are oriented axial rather than equatorial. Consequently, substituted cyclohexanes will preferentially adopt conformations in which the larger substituents assume equatorial orientation.

When the methyl group in the structure above occupies an axial position it suffers steric crowding by the two axial hydrogens located on the same side of the ring.

The conformation in which the methyl group is equatorial is more stable, and thus the equilibrium lies in this direction.
The relative steric hindrance experienced by different substituent groups oriented in an axial versus equatorial location on cyclohexane may be determined by the conformational equilibrium of the compound. The corresponding equilibrium constant is related to the energy difference between the conformers, and collecting such data allows us to evaluate the relative tendency of substituents to exist in an equatorial or axial location.A table of these free energy values (sometimes referred to as A values) may be examined by clicking here.
Looking at the energy values in this table, it is clear that the apparent "size" of a substituent (in terms of its preference for equatorial over axial orientation) is influenced by its width and bond length to cyclohexane, as evidenced by the fact that an axial vinyl group is less hindered than ethyl, and iodine slightly less than chlorine.
We noted earlier that cycloalkanes having two or more substituents on different ring carbon atoms exist as a pair (sometimes more) of configurational stereoisomers. Now we must examine the way in which favorable ring conformations influence the properties of the configurational isomers. Remember, configurational stereoisomers are stable and do not easily interconvert, whereas, conformational isomers normally interconvert rapidly. In examining possible structures for substituted cyclohexanes, it is useful to follow two principles:
(i) Chair conformations are generally more stable than other possibilities.
(ii) Substituents on chair conformers prefer to occupy equatorial positions due to the increased steric hindrance of axial locations.
The following equations and formulas illustrate how the presence of two or more substituents on a cyclohexane ring perturbs the interconversion of the two chair conformers in ways that can be predicted.
In the case of 1,1-disubstituted cyclohexanes, one of the substituents must necessarily be axial and the other equatorial, regardless of which chair conformer is considered. Since the substituents are the same in 1,1-dimethylcyclohexane, the two conformers are identical and present in equal concentration. In 1-t-butyl-1-methylcyclohexane the t-butyl group is much larger than the methyl, and that chair conformer in which the larger group is equatorial will be favored in the equilibrium( > 99%). Consequently, the methyl group in this compound is almost exclusively axial in its orientation.
In the cases of 1,2-, 1,3- and 1,4-disubstituted compounds the analysis is a bit more complex. It is always possible to have both groups equatorial, but whether this requires a cis-relationship or a trans-relationship depends on the relative location of the substituents. As we count around the ring from carbon #1 to #6, the uppermost bond on each carbon changes its orientation from equatorial (or axial) to axial (or equatorial) and back. It is important to remember that the bonds on a given side of a chair ring-conformation always alternate in this fashion. Therefore, it should be clear that for cis-1,2-disubstitution, one of the substituents must be equatorial and the other axial; in the trans-isomer both may be equatorial. Because of the alternating nature of equatorial and axial bonds, the opposite relationship is true for 1,3-disubstitution (cis is all equatorial, trans is equatorial/axial).
Finally, 1,4-disubstitution reverts to the 1,2-pattern:
The above analysis is not something that you should try to memorize: rather, become comfortable with drawing cyclohexane in the chair conformation, with bonds pointing in the correct directions for axial and equatorial substituents. If you can draw a structure correctly in the chair conformation, you should always be able to determine which positions are axial and which are equatorial.
Further Reading on Cyclohexanes
MasterOrganicChemistry
The ups and downs of cyclohexanes
Carey 4th Edition On-Line Activity
Khan Academy
Conformation of cyclohexane I: Chair and Boat
Web Pages
GOOD Extensive information about cyclohexane conformations
Videos
Axial vs Equitorial Position pt 1
Axial vs Equitorial Position pt 2
Tutorial
Drawing Chairs in 3D
Axial and Equitorial positions in cyclohexanes
Viewing and Drawing Chair conformations
Conformations of monosubstituted cyclohexanes
Carey 4th Edition On-Line Activity
Conformations of Substituted Cyclohexanes
Khan Academy
Conformation of Cyclohexane II: Monosubstituted
Web Pages

