6.3: Electrophilic Addition

We said that the highest energy pair of electrons (or HOMO) in alkenes is the \(π_{C-C}\). Thus, it should be the first thing to react in a chemical reaction. In an electrophilic addition, there is net addition of H-X across the \(π\) system. The \(π_{C-C}\) (HOMO) acts as the nucleophile in search for an empty orbital (LUMO). In the case of electrophilic addition, it finds that empty orbital in the form of a \(σ^{*}_{H-X}\) bond. The mechanism for electrophilic addition is a three-step process:

1. protonation of the double bond
2. formation of the carbocation
3. trapping of the atomic p orbital with X^–

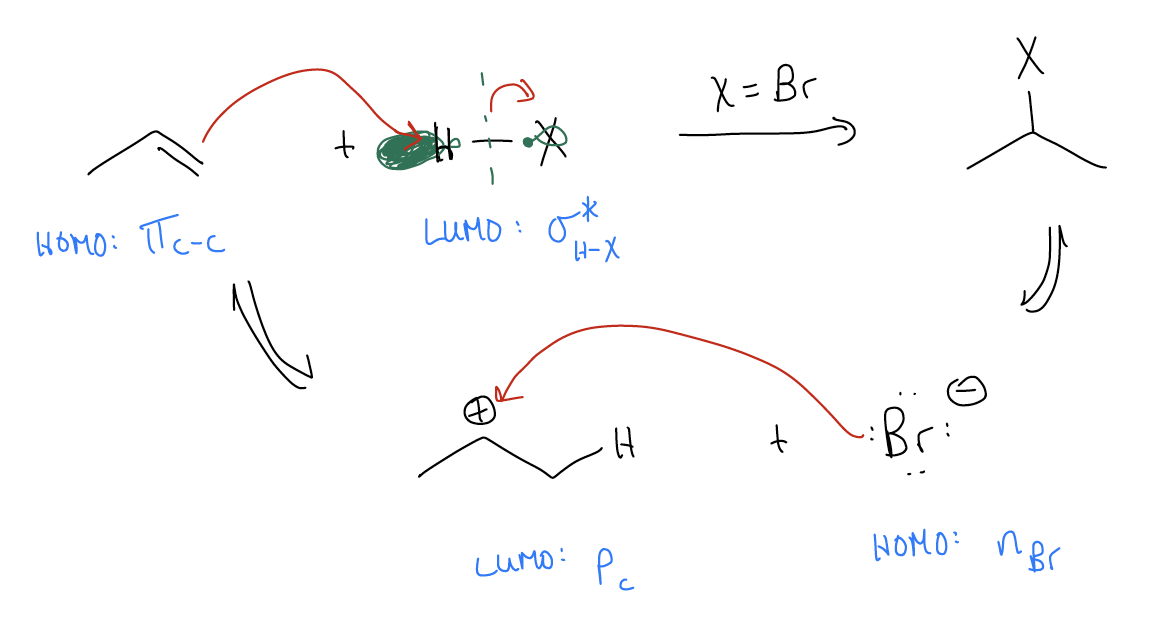
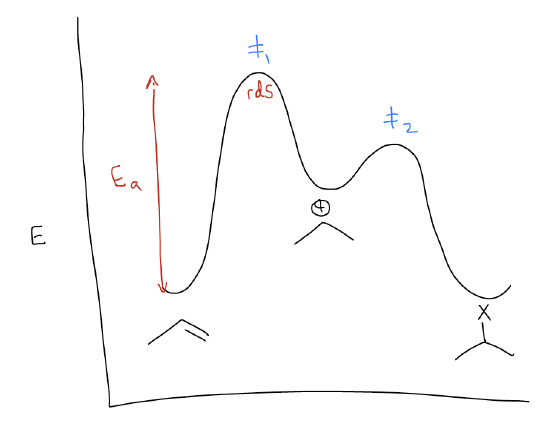
The reaction energy diagram (or reaction coordinate diagram) shows us that there is a larger activation barrier for the first set of arrows. Remember that a transition state is a local energy maximum that exhibits simultaneous bond-forming and bond-breaking events. In this case, the transition state brings together the alkene and the H-X. Once the alkene is protonated, the reaction funnels into a slightly lower energy well. This is known as the carbocation. The next set of arrows (where n_X is the HOMO and atomic p is the LUMO) is also a high energy transition state, but slightly lower than the first. The net result is an isopropyl halide as product. Recall that the rate determining step of this reaction is simply the step that contains the highest energy barrier. In this case, it is the protonation step, before the carbocation is even formed. Nothing after that event matters to the overall rate of the reaction.

You might be thinking about this reaction and wondering why we protonated the alkene the way we did. We certainly could have protonated the central carbon, leaving the positive formal charge on the terminal position. The difference would be that we would create a 1^o carbocation vs. a 2^o carbocation. If we were to draw the mechanism, it would look quite similar. The only difference is the position of the protonation, and the location of the nucleophilic attack of X^–.

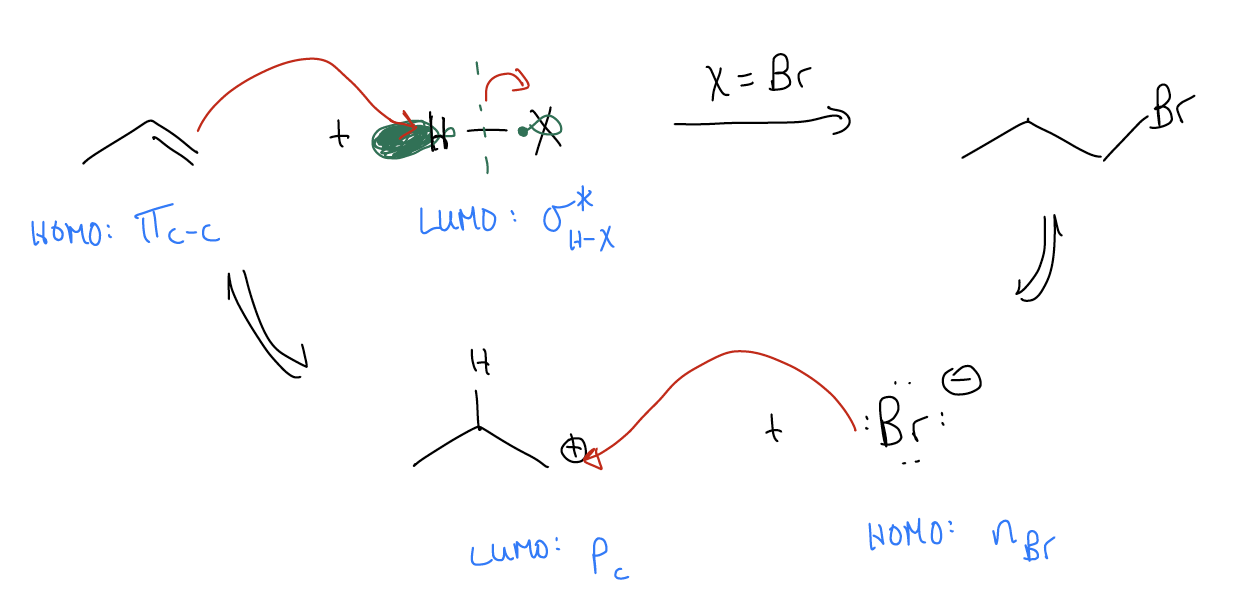
The reaction coordinate diagram would also look similar, with two key differences.

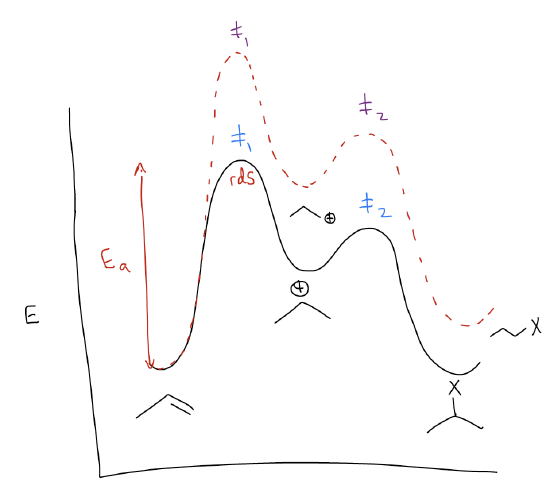
The first key difference is that the 1^o carbocation is higher in energy than the 2^o carbocation. If we extrapolate, we would see that the trend is that 3^o carbocations are the most stable.

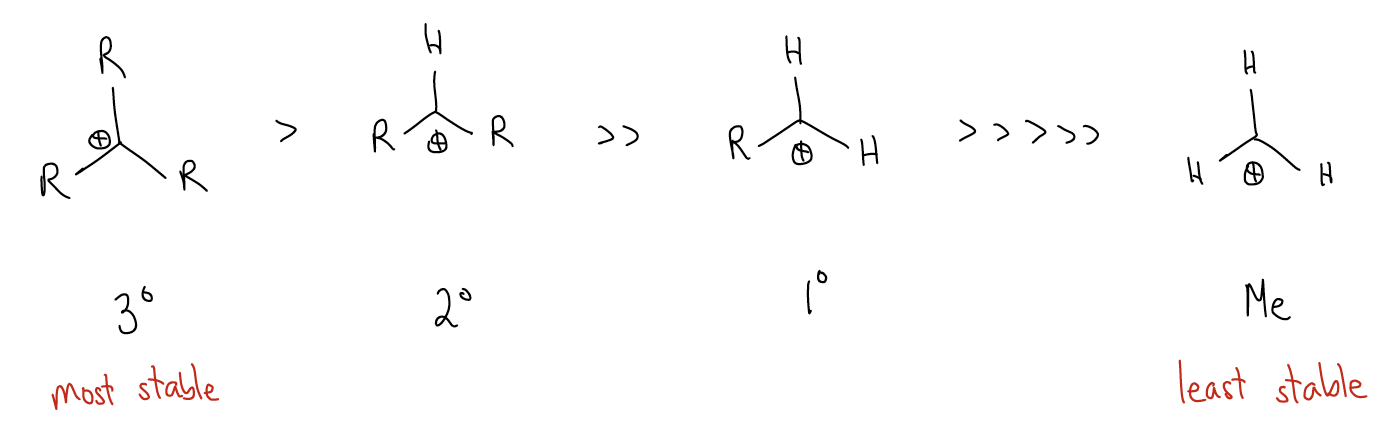
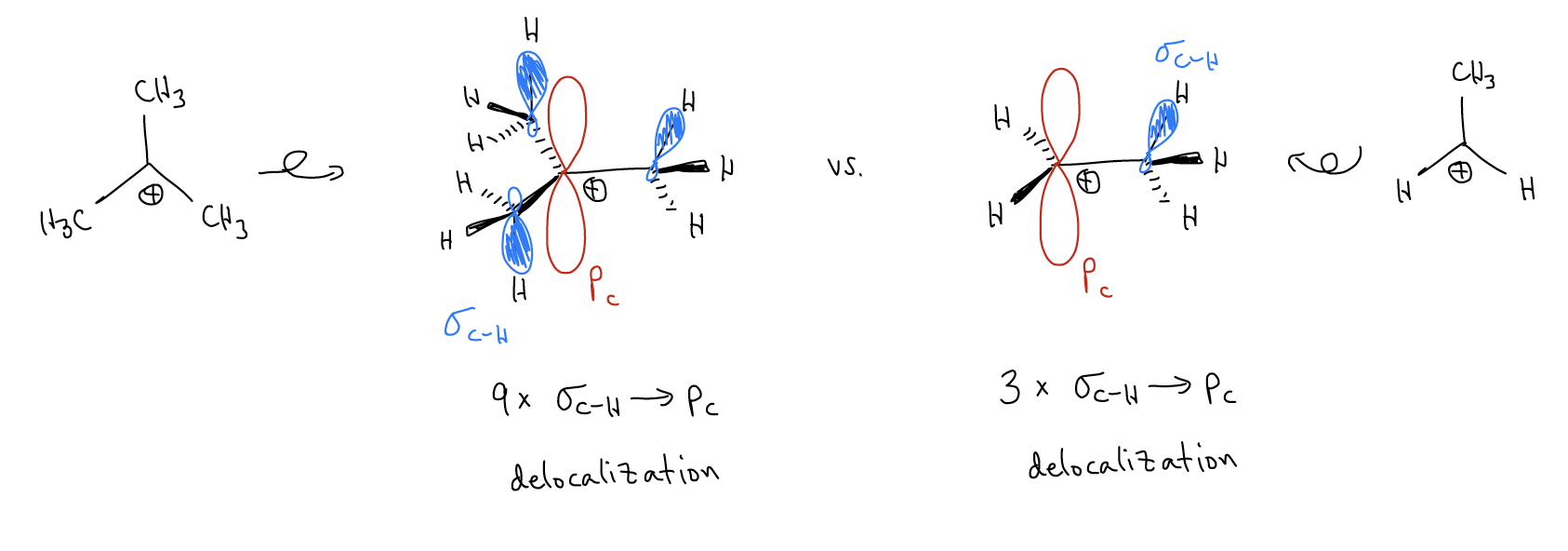
So, what accounts for this difference in stability? Again, our good friend \(σ\)-donation is at it again. Consider the following two carbocations. In the first carbocation, we have \(σ_{C-H}\) bonds that can delocalize into the atomic p orbital. This stabilizes the positive charge at that carbon atom. For a 3^o carbocation, this type of \(σ\)-donation occurs nine times. In a 1^o carbocation, it only occurs three times. Thus, there is a much greater effect with greater substitution.

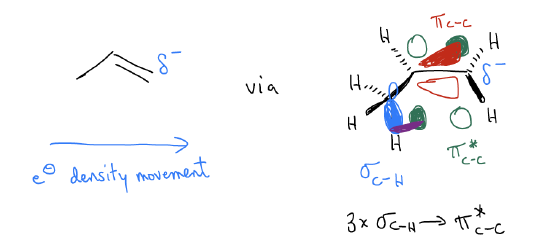
Along these lines, we must consider why the protonation occurs on the terminal carbon in the first place. After all, it is the transition state that determines the initial bond-formation to the proton – it has nothing to do with carbocation formation because that occurs later in the mechanism. Let’s take a look at the molecular orbital description of 1-propene and see if we can account for this regiochemistry. There are two possible regioisomers that can form in this reaction: isopropyl halide and n-propyl halide. Regiochemistry is a property of reactions that asks us to determine which of two possible sites will react. To confirm the regiochemical outcome of this reaction, let us recall the \(σ\)-donation that occurs in the alkene. 1-Propene is not a symmetrical system, so we should not expect that the p system is symmetrical. It should be polarized to one or the other side. Because there is \(σ\)-donation between the \(σ_{C-H}\) bonds and the \(π^{*}_{C-C}\), partially populating this orbital will shift electron density to the right (think of it as partially breaking the \(π_{C-C}\) bond, with electrons continuing to move along the chain). Thus, we should have electron density depositing on the terminal carbon. We say that the \(π_{C-C}\) bond is polarized towards the terminal carbon. It has greater electron density and will have a greater coefficient in the wavefunction. Since it has greater electron density, it is slightly more negatively charged and is bigger, which helps decrease the energy of the transition state – you get much better orbital overlap under these conditions.

While this explains the regiochemistry of the electrophilic addition, you still might not understand why the transition state leading to the 1^o carbocation is higher in energy. Thus, the second key difference in the reaction coordinate diagram is that the height of the first transition state is much greater for the formation of the 1^o carbocation. This can also be explained by \(σ\)-donation. This time, mixing between the \(σ_{C-H}\) orbitals and the \(π_{C-C}\) will create two new molecular orbitals in which the \(π_{C-C}\) increases in energy. This makes more highly substituted alkenes more reactive than less highly substituted alkenes – the HOMO is higher in energy and more reactive. In the transition state, this matters because now the two reactants don’t require as much kinetic energy to react. In essence, they’re already preprogrammed to find each other quicker. This takes less energy, driving down the energy of the transition state.

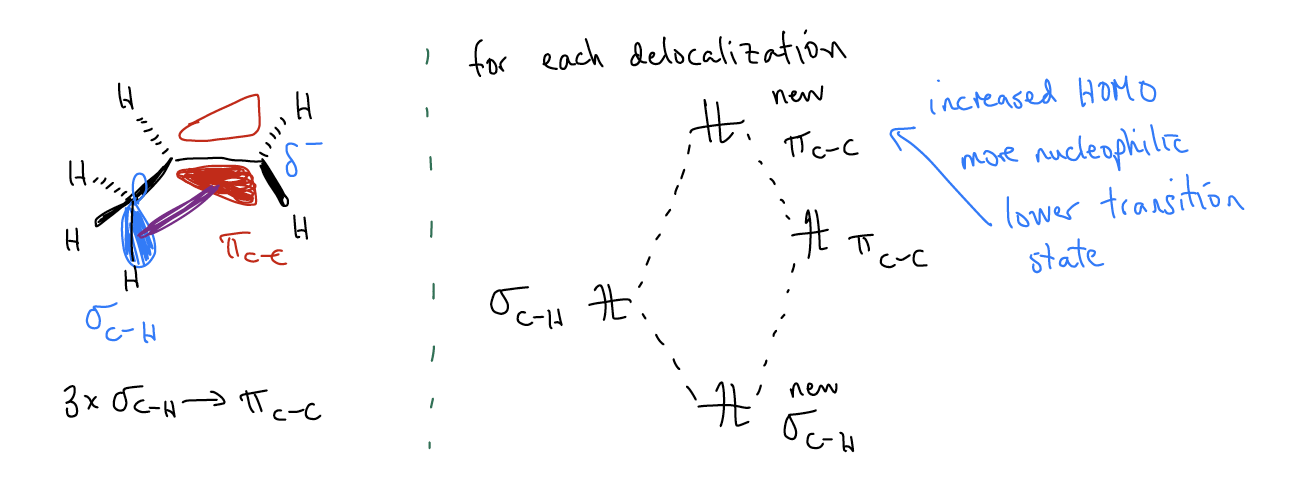
In summary, \(σ\)-donation has the effect of both decreasing the energy of the carbocation AND the initial transition state. Another truism is that more highly substituted alkenes are both more stable AND more reactive. This might seem counterintuitive, but remember that these are two very different things. Stability is a thermodynamic phenomenon, while reactivity is a kinetic phenomenon. It happens that both things are working in concert in this reaction to give you the same product, but it doesn’t always have to be this way.