Chapter 15.4: Hess's Law
- Page ID
- 42027
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\) |
Prince George's Community College |
 |
| Unit I: Atoms Unit II: Molecules Unit III: States of Matter Unit IV: Reactions Unit V: Kinetics & Equilibrium Unit VI: Thermo & Electrochemistry Unit VII: Nuclear Chemistry |
||
Learning Objectives
- To use Hess’s law and thermochemical cycles to calculate enthalpy changes of chemical reactions.
Hess’s Law
Because enthalpy is a state function, the enthalpy change for a reaction depends on only two things: (1) the masses of the reacting substances and (2) the physical states of the reactants and products. It does not depend on the path by which reactants are converted to products. If you climbed a mountain, for example, the altitude change would not depend on whether you climbed the entire way without stopping or you stopped many times to take a break. If you stopped often, the overall change in altitude would be the sum of the changes in altitude for each short stretch climbed. Similarly, when we add two or more balanced chemical equations to obtain a net chemical equation, ΔH for the net reaction is the sum of the ΔH values for the individual reactions. This principle is called Hess’s lawThe enthalpy change ΔH for an overall reaction is the sum of the ΔH values for the individual reactions., after the Swiss-born Russian chemist Germain Hess (1802–1850), a pioneer in the study of thermochemistry. Hess’s law allows us to calculate ΔH values for reactions that are difficult to carry out directly by adding together the known ΔH values for individual steps that give the overall reaction, even though the overall reaction may not actually occur via those steps.
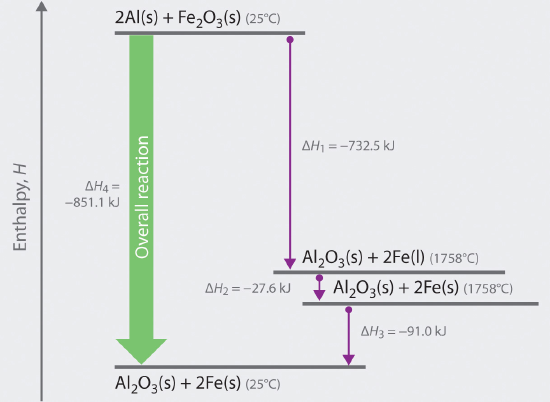
We can illustrate Hess’s law using the thermite reaction. The overall reaction shown in Equation 15.4.1 can be viewed as occurring in three distinct steps with known ΔH values. As shown in Figure 15.4.1, the first reaction produces 1 mol of solid aluminum oxide (Al2O3) and 2 mol of liquid iron at its melting point of 1758°C (part (a) in Equation 15.4.1); the enthalpy change for this reaction is −732.5 kJ/mol of Fe2O3. The second reaction is the conversion of 2 mol of liquid iron at 1758°C to 2 mol of solid iron at 1758°C (part (b) in Equation 15.4.1); the enthalpy change for this reaction is −13.8 kJ/mol of Fe (−27.6 kJ per 2 mol Fe). In the third reaction, 2 mol of solid iron at 1758°C is converted to 2 mol of solid iron at 25°C (part (c) in Equation 15.4.1); the enthalpy change for this reaction is −45.5 kJ/mol of Fe (−91.0 kJ per 2 mol Fe). As you can see in Figure 15.4.1, the overall reaction is given by the longest arrow (shown on the left), which is the sum of the three shorter arrows (shown on the right). Adding parts (a), (b), and (c) in Equation 15.4.1 gives the overall reaction, shown in part (d):
\( \begin{matrix}
2Al\left ( s, \; 25 ^{o}C \right ) + 2Fe_{2}O_{3}\left ( s, \; 25 ^{o}C \right )& \rightarrow & 2Fe\left ( l, \; 1758 ^{o}C \right ) + 2Al\left ( s, \; 1758 ^{o}C \right ) & \Delta H=-732.5 \; kJ& \left ( a \right ) \\
2Fe\left ( l, \; 1758 ^{o}C \right ) & \rightarrow & 2Fe\left ( s, \; 1758 ^{o}C \right ) & \Delta H=-\;\; 27.6 \; kJ & \left ( b \right )\\
2Fe\left ( s, \; 1758 ^{o}C \right ) + 2Al\left ( s, \; 1758 ^{o}C \right ) & \rightarrow & 2Fe\left ( l, \; 25 ^{o}C \right ) + 2Al\left ( s, \; 25 ^{o}C \right ) & \Delta H=-\;\; 91.0 \; kJ & \left ( c \right )\\
2Al\left ( s, \; 25 ^{o}C \right ) + 2Fe_{2}O_{3}\left ( s, \; 25 ^{o}C \right ) & \rightarrow & 2Al\left ( s, \; 25 ^{o}C \right ) + 2Fe_{2}O_{3}\left ( s, \; 25 ^{o}C \right ) & \Delta H=-852.2 \; kJ & \left ( d \right )
\end{matrix} \tag{15.4.1} \)
By Hess’s law, the enthalpy change for part (d) is the sum of the enthalpy changes for parts (a), (b), and (c). In essence, Hess’s law enables us to calculate the enthalpy change for the sum of a series of reactions without having to draw a diagram like that in Figure 15.4.1.
Figure 15.4.1 Energy Changes Accompanying the Thermite Reaction Because enthalpy is a state function, the overall enthalpy change for the reaction of 2 mol of Al(s) with 1 mol of Fe2O3(s) is −851.1 kJ, whether the reaction occurs in a single step (ΔH4, shown on the left) or in three hypothetical steps (shown on the right) that involve the successive formation of solid Al2O3 and liquid iron (ΔH1), solid iron at 1758°C (ΔH2), and solid iron at 25°C (ΔH3). Thus ΔH4 = ΔH1 + ΔH2 + ΔH3, as stated by Hess’s law.
Comparing parts (a) and (d) in Equation 15.4.1 also illustrates an important point: The magnitude of ΔH for a reaction depends on the physical states of the reactants and the products (gas, liquid, solid, or solution). When the product is liquid iron at its melting point (part (a) in Equation 15.4.1), only 732.5 kJ of heat are released to the surroundings compared with 852 kJ when the product is solid iron at 25°C (part (d) in Equation 15.4.1). The difference, 120 kJ, is the amount of energy that is released when 2 mol of liquid iron solidifies and cools to 25°C. It is important to specify the physical state of all reactants and products when writing a thermochemical equation.
When using Hess’s law to calculate the value of ΔH for a reaction, follow this procedure:
- Identify the equation whose ΔH value is unknown and write individual reactions with known ΔH values that, when added together, will give the desired equation.
- Arrange the chemical equations so that the reaction of interest is the sum of the individual reactions.
- If a reaction must be reversed, change the sign of ΔH for that reaction. Additionally, if a reaction must be multiplied by a factor to obtain the correct number of moles of a substance, multiply its ΔH value by that same factor.
- Add together the individual reactions and their corresponding ΔH values to obtain the reaction of interest and the unknown ΔH.
We illustrate how to use this procedure in Example 3.
Example 15.4.1
When carbon is burned with limited amounts of oxygen gas (O2), carbon monoxide (CO) is the main product:
\( \left ( 1 \right ) \;2C\left ( s \right ) + O_{2}\left ( g \right ) \rightarrow 2CO\left ( g \right ) \; \;\ \; \Delta H=-221.0 \; kJ \)
When carbon is burned in excess O2, carbon dioxide (CO2) is produced:
\( \left ( 2 \right ) \;C\left ( s \right ) + O_{2}\left ( g \right ) \rightarrow CO_{2}\left ( g \right ) \; \;\ \; \Delta H=-393.5 \; kJ \)
Use this information to calculate the enthalpy change per mole of CO for the reaction of CO with O2 to give CO2.
Given: two balanced chemical equations and their ΔH values
Asked for: enthalpy change for a third reaction
Strategy:
A After balancing the chemical equation for the overall reaction, write two equations whose ΔH values are known and that, when added together, give the equation for the overall reaction. (Reverse the direction of one or more of the equations as necessary, making sure to also reverse the sign of ΔH.)
B Multiply the equations by appropriate factors to ensure that they give the desired overall chemical equation when added together. To obtain the enthalpy change per mole of CO, write the resulting equations as a sum, along with the enthalpy change for each.
Solution:
A We begin by writing the balanced chemical equation for the reaction of interest:
\( \left ( 3 \right ) \;CO\left ( g \right ) + \frac{1}{2}O_{2}\left ( g \right ) \rightarrow CO_{2}\left ( g \right ) \; \;\ \; \Delta H_{rxn}=? \)
There are at least two ways to solve this problem using Hess’s law and the data provided. The simplest is to write two equations that can be added together to give the desired equation and for which the enthalpy changes are known. Observing that CO, a reactant in Equation 3, is a product in Equation 1, we can reverse Equation (1) to give
\( 2CO\left ( g \right ) \rightarrow 2C\left ( s \right ) + O_{2}\left ( g \right ) \; \;\ \; \Delta H=+221.0 \; kJ \)
Because we have reversed the direction of the reaction, the sign of ΔH is changed. We can use Equation 2 as written because its product, CO2, is the product we want in Equation 3:
\( C\left ( s \right ) + O_{2}\left ( g \right ) \rightarrow CO_{2}\left ( s \right ) \; \;\ \; \Delta H=-393.5 \; kJ \)
B Adding these two equations together does not give the desired reaction, however, because the numbers of C(s) on the left and right sides do not cancel. According to our strategy, we can multiply the second equation by 2 to obtain 2 mol of C(s) as the reactant:
\( 2C\left ( s \right ) + 2O_{2}\left ( g \right ) \rightarrow 2CO_{2}\left ( s \right ) \; \;\ \; \Delta H=-787.0 \; kJ \)
Writing the resulting equations as a sum, along with the enthalpy change for each, gives
\( \begin{matrix}
2CO\left ( g \right ) & \rightarrow & \cancel{2C\left ( s \right )}+\cancel{O_{2}\left ( g \right )} & \Delta H & = & -\Delta H_{1} & = & +221.0 \; kJ \\
\cancel{2C\left ( s \right )}+\cancel{2}O_{2}\left ( g \right ) & \rightarrow & 2CO_{2} \left ( g \right ) & \Delta H & = & -\Delta 2H_{2} & = & -787.0 \; kJ \\
2CO\left ( g \right ) + O_{2}\left ( g \right ) & \rightarrow & 2CO_{2} \left ( g \right ) & \Delta H & = & & -566.0 \; kJ
\end{matrix} \)
Note that the overall chemical equation and the enthalpy change for the reaction are both for the reaction of 2 mol of CO with O2, and the problem asks for the amount per mole of CO. Consequently, we must divide both sides of the final equation and the magnitude of ΔH by 2:
\( \begin{matrix}
CO\left ( g \right ) + \frac{1}{2}O_{2}\left ( g \right ) & \rightarrow & CO_{2} \left ( g \right ) & \Delta H & = & & -283.0 \; kJ
\end{matrix} \)
An alternative and equally valid way to solve this problem is to write the two given equations as occurring in steps. Note that we have multiplied the equations by the appropriate factors to allow us to cancel terms:
\( \begin{matrix}
\left ( A \right ) & 2C\left ( s \right ) + O_{2}\left ( g \right ) & \rightarrow & \cancel{2CO\left ( g \right )} & \Delta H_{A} & = & \Delta H_{1} & = & +221.0 \; kJ \\
\left ( B \right ) &\cancel{2CO\left ( g \right )} + O_{2}\left ( g \right ) & \rightarrow & 2CO_{2} \left ( g \right ) & \Delta H_{B} & & & = & ? \\
\left ( C \right ) & 2C\left ( s \right ) + 2O_{2}\left ( g \right ) & \rightarrow & 2CO_{2} \left ( g \right ) & \Delta H & = 2\Delta H_{2} & =2\times \left ( -393.5 \; kJ \right ) & =-787.0 \; kJ
\end{matrix} \)
The sum of reactions A and B is reaction C, which corresponds to the combustion of 2 mol of carbon to give CO2. From Hess’s law, ΔHA + ΔHB = ΔHC, and we are given ΔH for reactions A and C. Substituting the appropriate values gives
\( \begin{matrix}
-221.0 \; kJ + \Delta H_{B} = -787.0 \; kJ \\
\Delta H_{B} = -566.0
\end{matrix} \)
This is again the enthalpy change for the conversion of 2 mol of CO to CO2. The enthalpy change for the conversion of 1 mol of CO to CO2 is therefore −566.0 ÷ 2 = −283.0 kJ/mol of CO, which is the same result we obtained earlier. As you can see, there may be more than one correct way to solve a problem.
Exercise
The reaction of acetylene (C2H2) with hydrogen (H2) can produce either ethylene (C2H4) or ethane (C2H6):
\( \begin{matrix}
C_{2}H_{2}\left ( g \right ) + H_{2}\left ( g \right ) \rightarrow C_{2}H_{4}\left ( g \right ) & \Delta H = -175.7 \; kJ/mol \; C_{2}H_{2} \\
C_{2}H_{2}\left ( g \right ) + 2H_{2}\left ( g \right ) \rightarrow C_{2}H_{6}\left ( g \right ) & \Delta H = -312.0 \; kJ/mol \; C_{2}H_{2}
\end{matrix} \)
What is ΔH for the reaction of C2H4 with H2 to form C2H6?
Answer: −136.3 kJ/mol of C2H4
Enthalpies of Reaction
Chapter 11 and Chapter 12 presented a wide variety of chemical reactions, and you learned how to write balanced chemical equations that include all the reactants and the products except heat. One way to report the heat absorbed or released would be to compile a massive set of reference tables that list the enthalpy changes for all possible chemical reactions, which would require an incredible amount of effort. Fortunately, Hess’s law allows us to calculate the enthalpy change for virtually any conceivable chemical reaction using a relatively small set of tabulated data, such as the following:
- Enthalpy of combustion (ΔHcomb)The change in enthalpy that occurs during a combustion reaction.: Enthalpy changes have been measured for the combustion of virtually any substance that will burn in oxygen; these values are usually reported as the enthalpy of combustion per mole of substance.
- Enthalpy of fusion (ΔHfus)The enthalpy change that acompanies the melting (fusion) of 1 mol of a substance.: The enthalpy change that accompanies the melting, or fusion, of 1 mol of a substance; these values have been measured for almost all the elements and for most simple compounds.
- Enthalpy of vaporization (ΔHvap)The enthalpy change that accompanies the vaporization of 1 mol of a substance.: The enthalpy change that accompanies the vaporization of 1 mol of a substance; these values have also been measured for nearly all the elements and for most volatile compounds.
- Enthalpy of solution (ΔHsoln)The change in enthalpy that occurs when a specified amount of solute dissolves in a given quantity of solvent.: The enthalpy change when a specified amount of solute dissolves in a given quantity of solvent.
Table 15.4.1 Enthalpies of Vaporization and Fusion for Selected Substances at Their Boiling Points and Melting Points
| Substance | ΔHvap (kJ/mol) | ΔHfus (kJ/mol) |
|---|---|---|
| argon (Ar) | 6.3 | 1.3 |
| methane (CH4) | 9.2 | 0.84 |
| ethanol (CH3CH2OH) | 39.3 | 7.6 |
| benzene (C6H6) | 31.0 | 10.9 |
| water (H2O) | 40.7 | 6.0 |
| mercury (Hg) | 59.0 | 2.29 |
| iron (Fe) | 340 | 14 |
Note the Pattern
The sign convention is the same for all enthalpy changes: negative if heat is released by the system and positive if heat is absorbed by the system.
Summary
For a chemical reaction, the enthalpy of reaction (ΔHrxn) is the difference in enthalpy between products and reactants; the units of ΔHrxn are kilojoules per mole. Reversing a chemical reaction reverses the sign of ΔHrxn. The magnitude of ΔHrxn also depends on the physical state of the reactants and the products because processes such as melting solids or vaporizing liquids are also accompanied by enthalpy changes: the enthalpy of fusion (ΔHfus) and the enthalpy of vaporization (ΔHvap), respectively. The overall enthalpy change for a series of reactions is the sum of the enthalpy changes for the individual reactions, which is Hess’s law. The enthalpy of combustion (ΔHcomb) is the enthalpy change that occurs when a substance is burned in excess oxygen.
Key Takeaway
- Hess's law: The overall enthalpy change for a series of reactions is the sum of the enthalpy changes for the individual reactions:
Conceptual Problems
-
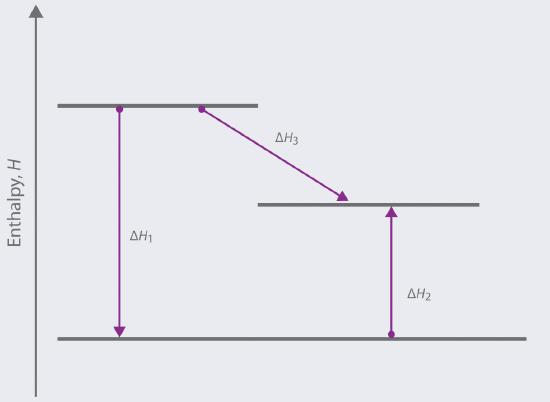
Based on the following energy diagram,
a. write an equation showing how the value of ΔH3 could be determined if the values of ΔH1 and ΔH2 are known.
b. identify each step as being exothermic or endothermic.
-
Describe how Hess’s law can be used to calculate the enthalpy change of a reaction that cannot be observed directly.
-
When you apply Hess’s law, what enthalpy values do you need to account for each change in physical state?
- the melting of a solid
- the conversion of a gas to a liquid
- the solidification of a liquid
- the dissolution of a solid into water
-
In their elemental form, A2 and B2 exist as diatomic molecules. Given the following reactions, each with an associated ΔH°, describe how you would calculate ΔHof for the compound AB2.
\( \begin{matrix}
2AB & \rightarrow & A_{2} + B _{2} & \Delta H_{1}^{o}\\
3AB & \rightarrow & AB_{2} + A _{2}B & \Delta H_{2}^{o} \\
2A_{2}B &\rightarrow & 2A_{2} + B _{2} & \Delta H_{3}^{o}
\end{matrix} \)
Numerical Problems
-
Methanol is used as a fuel in Indianapolis 500 race cars. Use the following table to determine whether methanol or 2,2,4-trimethylpentane (isooctane) releases more energy per liter during combustion.
Fuel ΔHocombustion(kJ/mol) Density (g/mL) methanol −726.1 0.791 2,2,4-trimethylpentane −5461.4 0.692 -
a. Use the enthalpies of combustion given in the following table to determine which organic compound releases the greatest amount of energy per gram during combustion.
Fuel ΔHocombustion(kJ/mol)
methanol −726.1 1-ethyl-2-methylbenzene −5210.2 n-octane −5470.5 b. Calculate the standard enthalpy of formation of 1-ethyl-2-methylbenzene.
-
Given the enthalpies of combustion, which organic compound is the best fuel per gram?
Fuel ΔHof(kJ/mol)
ethanol −1366.8 benzene −3267.6 cyclooctane −5434.7
Answers
1.
2.
a. To one decimal place
methanol: ΔH/g = −22.6 kJ
C9H12: ΔH/g = −43.3 kJ
octane: ΔH/g = −47.9 kJ
Octane provides the largest amount of heat per gram upon combustion.
b, ΔHf(C9H17) = −46.1 kJ/mol
Contributors
- Anonymous
Modified by Joshua Halpern (Howard University), Scott Sinex, and Scott Johnson (PGCC)