Chapter 7.1: Real Gases
- Page ID
- 42075
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\) |
Prince George's Community College |
 |
| Unit I: Atoms Unit II: Molecules Unit III: States of Matter Unit IV: Reactions Unit V: Kinetics & Equilibrium Unit VI: Thermo & Electrochemistry Unit VII: Nuclear Chemistry |
||
Learning Objective
- To recognize the differences between the behavior of an ideal gas and a real gas.
The postulates of the kinetic molecular theory of gases ignore both the volume occupied by the molecules of a gas and all interactions between molecules, whether attractive or repulsive. In reality, however, all gases have nonzero molecular volumes. Furthermore, the molecules of real gases interact with one another in ways that depend on the structure of the molecules and therefore differ for each gaseous substance. In this section, we consider the properties of real gases and how and why they differ from the predictions of the ideal gas law. We also examine liquefaction, a key property of real gases that is not predicted by the kinetic molecular theory of gases.
Pressure, Volume, and Temperature Relationships in Real Gases
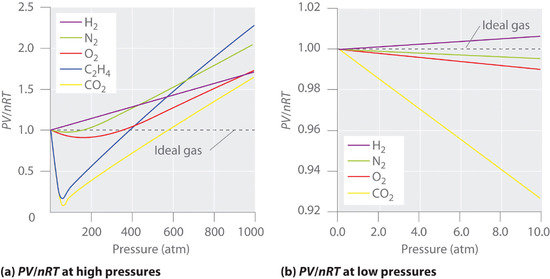
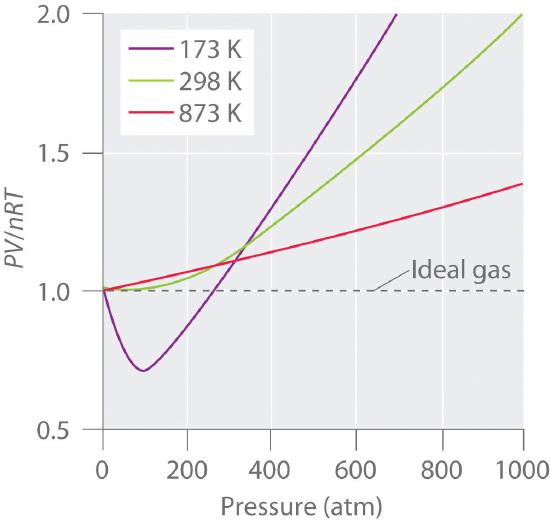
For an ideal gas, a plot of PV/nRT versus P gives a horizontal line with an intercept of 1 on the PV/nRT axis. Real gases, however, show significant deviations from the behavior expected for an ideal gas, particularly at high pressures (part (a) in Figure 7.1.1 ). Only at relatively low pressures (less than 1 atm) do real gases approximate ideal gas behavior (part (b) in Figure 7.1.1 ). Real gases also approach ideal gas behavior more closely at higher temperatures, as shown in Figure 7.1.2 for N2. Why do real gases behave so differently from ideal gases at high pressures and low temperatures? Under these conditions, the two basic assumptions behind the ideal gas law—namely, that gas molecules have negligible volume and that intermolecular interactions are negligible—are no longer valid.
Figure 7.1.1 Real Gases Do Not Obey the Ideal Gas Law, Especially at High Pressures (a) In these plots of PV/nRT versus P at 273 K for several common gases, there are large negative deviations observed for C2H4 and CO2 because they liquefy at relatively low pressures. (b) These plots illustrate the relatively good agreement between experimental data for real gases and the ideal gas law at low pressures.
Figure 7.1.2 The Effect of Temperature on the Behavior of Real Gases A plot of PV/nRT versus P for nitrogen gas at three temperatures shows that the approximation to ideal gas behavior becomes better as the temperature increases.
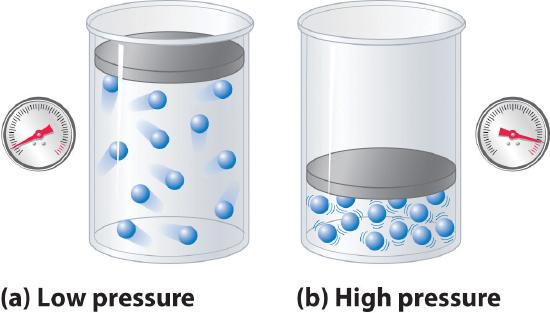
Because the molecules of an ideal gas are assumed to have zero volume, the volume available to them for motion is always the same as the volume of the container. In contrast, the molecules of a real gas have small but measurable volumes. At low pressures, the gaseous molecules are relatively far apart, but as the pressure of the gas increases, the intermolecular distances become smaller and smaller (Figure 7.1.3). As a result, the volume occupied by the molecules becomes significant compared with the volume of the container. Consequently, the total volume occupied by the gas is greater than the volume predicted by the ideal gas law. Thus at very high pressures, the experimentally measured value of PV/nRT is greater than the value predicted by the ideal gas law.
Figure 7.1.3 The Effect of Nonzero Volume of Gas Particles on the Behavior of Gases at Low and High Pressures (a) At low pressures, the volume occupied by the molecules themselves is small compared with the volume of the container. (b) At high pressures, the molecules occupy a large portion of the volume of the container, resulting in significantly decreased space in which the molecules can move.
Moreover, all molecules are attracted to one another by a combination of forces. These forces become particularly important for gases at low temperatures and high pressures, where intermolecular distances are shorter. Attractions between molecules reduce the number of collisions with the container wall, an effect that becomes more pronounced as the number of attractive interactions increases. Because the average distance between molecules decreases, the pressure exerted by the gas on the container wall decreases, and the observed pressure is less than expected (Figure 7.1.4). Thus as shown in Figure 7.1.2, at low temperatures, the ratio of PV/nRT is lower than predicted for an ideal gas, an effect that becomes particularly evident for complex gases and for simple gases at low temperatures. At very high pressures, the effect of nonzero molecular volume predominates. The competition between these effects is responsible for the minimum observed in the PV/nRT versus P plot for many gases.
Note the Pattern
Nonzero molecular volume makes the actual volume greater than predicted at high pressures; intermolecular attractions make the pressure less than predicted.
At high temperatures, the molecules have sufficient kinetic energy to overcome intermolecular attractive forces, and the effects of nonzero molecular volume predominate. Conversely, as the temperature is lowered, the kinetic energy of the gas molecules decreases. Eventually, a point is reached where the molecules can no longer overcome the intermolecular attractive forces, and the gas liquefies (condenses to a liquid).
The van der Waals Equation
The Dutch physicist Johannes van der Waals (1837–1923; Nobel Prize in Physics, 1910) modified the ideal gas law to describe the behavior of real gases by explicitly including the effects of molecular size and intermolecular forces. In his description of gas behavior, the so-called van der Waals equationA modification of the ideal gas law designed to describe the behavior of real gases by explicitly including the effects of molecular volume and intermolecular forces.,
\[ \left ( P+\dfrac{an^{2}}{V^{2}} \right )\left ( V-nb \right )=nRT \tag{7.1.1} \]
a and b are empirical constants that are different for each gas. The values of a and b are listed in Table 7.1.1 for several common gases. The pressure term P + (an2/V2) corrects for intermolecular attractive forces that tend to reduce the pressure from that predicted by the ideal gas law. Here, n2/V2 represents the concentration of the gas (n/V) squared because it takes two particles to engage in the pairwise intermolecular interactions of the type shown in Figure 7.1.4 . The volume term V − nb corrects for the volume occupied by the gaseous molecules.
Table 7.1.1 van der Waals Constants for Some Common Gases
| Gas | a (L2·atm)/mol2) | b (L/mol) |
|---|---|---|
| He | 0.03410 | 0.0238 |
| Ne | 0.205 | 0.0167 |
| Ar | 1.337 | 0.032 |
| H2 | 0.2420 | 0.0265 |
| N2 | 1.352 | 0.0387 |
| O2 | 1.364 | 0.0319 |
| Cl2 | 6.260 | 0.0542 |
| NH3 | 4.170 | 0.0371 |
| CH4 | 2.273 | 0.0430 |
| CO2 | 3.610 | 0.0429 |
Figure 7.1.4 The Effect of Intermolecular Attractive Forces on the Pressure a Gas Exerts on the Container Walls (a) At low pressures, there are relatively few attractive intermolecular interactions to lessen the impact of the molecule striking the wall of the container, and the pressure is close to that predicted by the ideal gas law. (b) At high pressures, with the average intermolecular distance relatively small, the effect of intermolecular interactions is to lessen the impact of a given molecule striking the container wall, resulting in a lower pressure than predicted by the ideal gas law.
The correction for volume is negative, but the correction for pressure is positive to reflect the effect of each factor on V and P, respectively. Because nonzero molecular volumes produce a measured volume that is larger than that predicted by the ideal gas law, we must subtract the molecular volumes to obtain the actual volume available. Conversely, attractive intermolecular forces produce a pressure that is less than that expected based on the ideal gas law, so the an2/V2 term must be added to the measured pressure to correct for these effects.
Example 7.1.1
You are in charge of the manufacture of cylinders of compressed gas at a small company. Your company president would like to offer a 4.0 L cylinder containing 500 g of chlorine in the new catalog. The cylinders you have on hand have a rupture pressure of 40 atm. Use both the ideal gas law and the van der Waals equation to calculate the pressure in a cylinder at 25°C. Is this cylinder likely to be safe against sudden rupture (which would be disastrous and certainly result in lawsuits because chlorine gas is highly toxic)?
Given: volume of cylinder, mass of compound, pressure, and temperature
Asked for: safety
Strategy:
A Use the molar mass of chlorine to calculate the amount of chlorine in the cylinder. Then calculate the pressure of the gas using the ideal gas law.
B Obtain a and b values for Cl2 from Table 7.1.1 . Use the van der Waals equation to solve for the pressure of the gas. Based on the value obtained, predict whether the cylinder is likely to be safe against sudden rupture.
Solution:
A We begin by calculating the amount of chlorine in the cylinder using the molar mass of chlorine (70.906 g/mol):
\( \left ( 500 \; \cancel{g} \right )\left ( \dfrac{1 \; mol}{70.906 \; \cancel{g}}=7.05 mol \; Cl_{2} \right ) \)
Using the ideal gas law and the temperature in kelvins (298 K), we calculate the pressure:
\( P=\dfrac{nRT}{V}=\dfrac{\left ( 7.05 \; \cancel{mol} \right )\left [ 0.08206\left ( \cancel{L}\cdot atm \right )/\left ( \cancel{K}\cdot \cancel{mol} \right ) \right ]\left ( 298 \; \cancel{K} \right )}{4.0 \; \cancel {L}}=43 \; atm \)
If chlorine behaves like an ideal gas, you have a real problem!
B Now let’s use the van der Waals equation with the a and b values for Cl2 from Table 7.1.1 . Solving for P gives
\( P= \dfrac{nRT}{V-nb}-\dfrac{an^{2}}{V^{2}} \)
\( =\dfrac{\left ( 7.05 \; \cancel{mol} \right )\left [ 0.08206\left ( \cancel{L}\cdot atm \right )/\left ( \cancel{K}\cdot \cancel{mol} \right ) \right ]\left ( 298 \; \cancel{K} \right )}{4.0 \; \cancel {L} - 7.05 \; \cancel{mol}\left ( 0.0542 \; \cancel{L}/\cancel{mol} \right )} - \dfrac{6.260^{2} \; \cancel{L^{2}}\cdot atm/\cancel{mol^{2}}\left ( 7.05 \; \cancel{mol^{2}} \right )}{4.0 \; \cancel{L^{2}}} \)
\( = 47.7 \; atm - 19.4 \; atm = 28 \; atm \;(2\; significant \; figures) \)
This pressure is well within the safety limits of the cylinder. The ideal gas law predicts a pressure 15 atm higher than that of the van der Waals equation.
Exercise
A 10.0 L cylinder contains 500 g of methane. Calculate its pressure to two significant figures at 27°C using the
- ideal gas law.
- van der Waals equation.
Answer: a. 77 atm; b. 67 atm
Liquefaction of Gases
LiquefactionThe condensation of gases into a liquid form. of gases is the condensation of gases into a liquid form, which is neither anticipated nor explained by the kinetic molecular theory of gases. Both the theory and the ideal gas law predict that gases compressed to very high pressures and cooled to very low temperatures should still behave like gases, albeit cold, dense ones. As gases are compressed and cooled, however, they invariably condense to form liquids, although very low temperatures are needed to liquefy light elements such as helium (for He, 4.2 K at 1 atm pressure).
Liquefaction can be viewed as an extreme deviation from ideal gas behavior. It occurs when the molecules of a gas are cooled to the point where they no longer possess sufficient kinetic energy to overcome intermolecular attractive forces. The precise combination of temperature and pressure needed to liquefy a gas depends strongly on its molar mass and structure, with heavier and more complex molecules usually liquefying at higher temperatures. In general, substances with large van der Waals a coefficients are relatively easy to liquefy because large a coefficients indicate relatively strong intermolecular attractive interactions. Conversely, small molecules with only light elements have small a coefficients, indicating weak intermolecular interactions, and they are relatively difficult to liquefy. Gas liquefaction is used on a massive scale to separate O2, N2, Ar, Ne, Kr, and Xe. After a sample of air is liquefied, the mixture is warmed, and the gases are separated according to their boiling points. In Section 7.2 , we will consider in more detail the nature of the intermolecular forces that allow gases to liquefy.
Note the Pattern
A large value of a indicates the presence of relatively strong intermolecular attractive interactions.
The ultracold liquids formed from the liquefaction of gases are called cryogenic liquids (an ultracold liquid formed from the liquefaction of gases., from the Greek kryo, meaning “cold,” and genes, meaning “producing”). They have applications as refrigerants in both industry and biology. For example, under carefully controlled conditions, the very cold temperatures afforded by liquefied gases such as nitrogen (boiling point = 77 K at 1 atm) can preserve biological materials, such as semen for the artificial insemination of cows and other farm animals. These liquids can also be used in a specialized type of surgery called cryosurgery, which selectively destroys tissues with a minimal loss of blood by the use of extreme cold.
Figure 7.1.6 Compressing and Distilling Air: this video from the Royal Society of Chemistry describes how air is liquefied by a combination of cooling and expansion and then distilled to yield liquid nitrogen, oxygen and argon
Moreover, the liquefaction of gases is tremendously important in the storage and shipment of fossil fuels. Liquefied natural gas (LNG) and liquefied petroleum gas (LPG) are liquefied forms of hydrocarbons produced from natural gas or petroleum reserves. LNG consists mostly of methane, with small amounts of heavier hydrocarbons; it is prepared by cooling natural gas to below about −162°C. It can be stored in double-walled, vacuum-insulated containers at or slightly above atmospheric pressure. Because LNG occupies only about 1/600 the volume of natural gas, it is easier and more economical to transport. LPG is typically a mixture of propane, propene, butane, and butenes and is primarily used as a fuel for home heating. It is also used as a feedstock for chemical plants and as an inexpensive and relatively nonpolluting fuel for some automobiles.
Figure 7.1.7 Liquefying Natural Gas: This video from Shell Oil describes the industrial process of liquefying natural gas
Summary
No real gas exhibits ideal gas behavior, although many real gases approximate it over a range of conditions. Deviations from ideal gas behavior can be seen in plots of PV/nRT versus P at a given temperature; for an ideal gas, PV/nRT versus P = 1 under all conditions. At high pressures, most real gases exhibit larger PV/nRT values than predicted by the ideal gas law, whereas at low pressures, most real gases exhibit PV/nRT values close to those predicted by the ideal gas law. Gases most closely approximate ideal gas behavior at high temperatures and low pressures. Deviations from ideal gas law behavior can be described by the van der Waals equation, which includes empirical constants to correct for the actual volume of the gaseous molecules and quantify the reduction in pressure due to intermolecular attractive forces. If the temperature of a gas is decreased sufficiently, liquefaction occurs, in which the gas condenses into a liquid form. Liquefied gases have many commercial applications, including the transport of large amounts of gases in small volumes and the uses of ultracold cryogenic liquids.
Key Takeaway
- Molecular volumes and intermolecular attractions cause the properties of real gases to deviate from those predicted by the ideal gas law.
Key Equation
van der Waals equation
Equation 7.1.1: \( \left ( p+\dfrac{an^{2}}{V^{2}} \right )\left ( V-b \right )=nRT \)<mi/>
Conceptual Problems
-
What factors cause deviations from ideal gas behavior? Use a sketch to explain your answer based on interactions at the molecular level.
-
Explain the effect of nonzero atomic volume on the ideal gas law at high pressure. Draw a typical graph of volume versus 1/P for an ideal gas and a real gas.
-
For an ideal gas, the product of pressure and volume should be constant, regardless of the pressure. Experimental data for methane, however, show that the value of PV decreases significantly over the pressure range 0 to 120 atm at 0°C. The decrease in PV over the same pressure range is much smaller at 100°C. Explain why PV decreases with increasing temperature. Why is the decrease less significant at higher temperatures.
-
What is the effect of intermolecular forces on the liquefaction of a gas? At constant pressure and volume, does it become easier or harder to liquefy a gas as its temperature increases? Explain your reasoning. What is the effect of increasing the pressure on the liquefaction temperature?
-
Describe qualitatively what a and b, the two empirical constants in the van der Waals equation, represent.
-
In the van der Waals equation, why is the term that corrects for volume negative and the term that corrects for pressure positive? Why is n/V squared?
-
Liquefaction of a gas depends strongly on two factors. What are they? As temperature is decreased, which gas will liquefy first—ammonia, methane, or carbon monoxide? Why?
-
What is a cryogenic liquid? Describe three uses of cryogenic liquids.
-
Air consists primarily of O2, N2, Ar, Ne, Kr, and Xe. Use the concepts discussed in this chapter to propose two methods by which air can be separated into its components. Which component of air will be isolated first?
-
How can gas liquefaction facilitate the storage and transport of fossil fuels? What are potential drawbacks to these methods?
Numerical Problems
-
The van der Waals constants for xenon are a = 4.19 (L2·atm)/mol2 and b = 0.0510 L/mol. If a 0.250 mol sample of xenon in a container with a volume of 3.65 L is cooled to −90°C, what is the pressure of the sample assuming ideal gas behavior? What would be the actual pressure under these conditions?
-
The van der Waals constants for water vapor are a = 5.46 (L2·atm)/mol2 and b = 0.0305 L/mol. If a 20.0 g sample of water in a container with a volume of 5.0 L is heated to 120°C, what is the pressure of the sample assuming ideal gas behavior? What would be the actual pressure under these conditions?