Chapter 6.7: Mean Free Path
- Page ID
- 43253
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\) |
Prince George's Community College |
 |
| Unit I: Atoms Unit II: Molecules Unit III: States of Matter Unit IV: Reactions Unit V: Kinetics & Equilibrium Unit VI: Thermo & Electrochemistry Unit VII: Nuclear Chemistry |
||
Learning Objective
- The mean free path is the average distance traveled by a moving molecule between collisions.
Introduction
Imagine gas leaking out of a pipe. It would take a while for the gas to diffuse and spread into the environment. This is because gas molecules collide with each other, causing them to change in speed and direction. Therefore, they can never move in a straight path without interruptions. Between every two consecutive collisions, a gas molecule travels a straight path. The average distance of all the paths of a molecule is the mean free path.
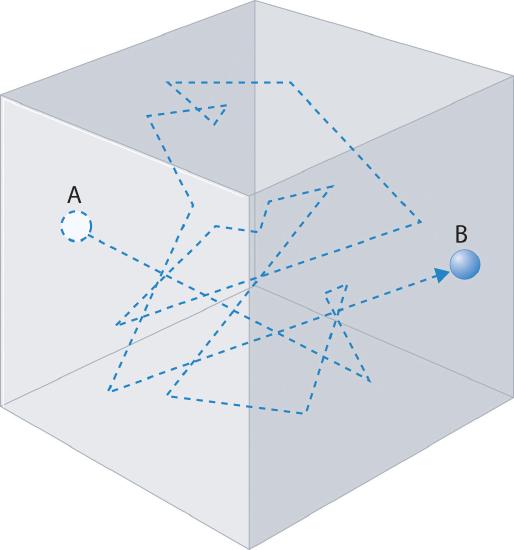
Gas molecules do not diffuse nearly as rapidly as their very high speeds might suggest. If molecules actually moved through a room at hundreds of miles per hour, we would detect odors faster than we hear sound. Instead, it can take several minutes for us to detect an aroma because molecules are traveling in a medium with other gas molecules. Because gas molecules collide as often as 1010 times per second, changing direction and speed with each collision, they do not diffuse across a room in a straight line, as illustrated schematically in Figure 6.7.1 The average distance traveled by a molecule between collisions is the mean free pathThe average distance traveled by a molecule between collisions.. The denser the gas, the shorter the mean free path; conversely, as density decreases, the mean free path becomes longer because collisions occur less frequently. At 1 atm pressure and 25°C, for example, an oxygen or nitrogen molecule in the atmosphere travels only about 6.0 × 10−8 m (60 nm) between collisions. In the upper atmosphere at about 100 km altitude, where gas density is much lower, the mean free path is about 10 cm; in space between galaxies, it can be as long as 1 × 1010 m (about 6 million miles).
Figure 6.7.1 The Path of a Single Particle in a Gas Sample The frequent changes in direction are the result of collisions with other gas molecules and with the walls of the container.
Calculations
In reality, the mean free path cannot be calculated by taking the average of all the paths because it is impossible to know the distance of each path traveled by a molecule. However, we can calculate it from the average speed (\(\langle c \rangle\)) of the molecule divided by the collision frequency (\(Z\)). The formula for this is:
\[\lambda = \dfrac{\langle c \rangle}{Z} \tag{6.7.1} \]
Because \(Z\) is equal to \(1/ t\), where \(t\) is the average time between collisions, the formula can also be:
\[\begin{eqnarray} \lambda &=& \dfrac{\langle c \rangle}{\dfrac{1}{t}} \\ &=& \langle c \rangle \times t \end{eqnarray} \tag{6.7.2} \]
In addition, because
\[\lambda = \sqrt{2} \pi d^2 \langle c \rangle (N/V) \tag{6.7.3} \]
where
- \(d\) is the diameter of the molecule and
- (\(N/V\)) is the density,
The formula can be further modified to:
\[ \begin{eqnarray} l &=& \dfrac{\langle c \rangle}{\sqrt{2} \pi d^2 \langle c \rangle \dfrac{N}{V}} \\ &=& \dfrac{1}{\sqrt{2} \pi d^2 \dfrac{N}{V}} \end{eqnarray} \tag{6.7.4} \]
Factors affecting mean free path
- Density: As gas density increases, the molecules become closer to each other. Therefore, they are more likely to run into each other, so the mean free path decreases.
- Increasing the number of molecules or decreasing the volume causes density to increase. This decreases the mean free path.
- Radius of molecule: Increasing the radii of the molecules decreases the space between them, causing them to run into each other more often. Therefore, the mean free path decreases.
- Pressure, temperature, and other factors that affect density can indirectly affect mean free path.
Practice Problems
- A gas has an average speed of 10 m/s and a collision frequency of 10 s-1. What is its mean free path?
- A gas has an average speed of 10 m/s and an average time of 0.1 s between collisions. What is its mean free path?
- A gas has a density of 10 particles m-3 and a molecular diameter of 0.1 m. What is its mean free path?
- A gas in a 1 m3 container has a molecular diameter of 0.1 m. There are 10 molecules. What is its mean free path?
- A gas has a molecular diameter of 0.1 m. It also has a mean free path of 2.25 m. What is its density?
Answers
- l = <c> / = 10 m/s / 10 s^(-1) = 1 m
- l = <c> X (average time between collisions) = 10 m/s X 0.1 s = 1 m
- l = 1 / [
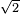 (pi) d^2 (N/v)] = 1 / [
(pi) d^2 (N/v)] = 1 / [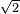 (pi)(0.1 m)^2 (10 m^(-3))] = 2.25 m
(pi)(0.1 m)^2 (10 m^(-3))] = 2.25 m - l = 1 / [
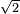 (pi) d^2 (N/v)] = 1 / [
(pi) d^2 (N/v)] = 1 / [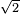 (pi)(0.1 m)^2 (10 / 1 m^3)] = 2.25 m
(pi)(0.1 m)^2 (10 / 1 m^3)] = 2.25 m - l = 1 / [
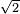 (pi) d^2 (N/v)]
(pi) d^2 (N/v)]
2.25 m = 1 / [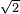 (pi)(0.1 m)^2 (N/v)]
(pi)(0.1 m)^2 (N/v)]
N/v = 10 m^(-3)
References
- Chang, Raymond. Physical Chemistry for the Biosciences. California: University Science Books, 2005.
- Atkins, Peter and Julio de Paula. Physical Chemistry for the Life Sciences. New York: Oxford University Press, 2006.
Contributors
- Tho Nguyen, Michael Dai