Chapter 6.4: The Combined Gas Law
- Page ID
- 42039
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\) |
Prince George's Community College |
 |
| Unit I: Atoms Unit II: Molecules Unit III: States of Matter Unit IV: Reactions Unit V: Kinetics & Equilibrium Unit VI: Thermo & Electrochemistry Unit VII: Nuclear Chemistry |
||
Learning Objective
- To understand the relationships among pressure, temperature, volume, and the amount of a gas.
We often encounter cases where two of the variables P, V, n and T are allowed to vary for a given sample of gas, and we are interested in the change in the value of the third under the new conditions. If we rearrange the ideal gas law so that P, V, and T, the quantities that change, are on one side and the constant terms (R and n for a given sample of gas) are on the other, we obtain
\( \dfrac{PV}{T}=nR = constant \tag{6.4.1} \)
Thus the quantity PV/nT is constant
\( \dfrac{P_{1}V_{1}}{n_{1}T_{1}}= \dfrac{P_{2}V_{2}}{n_{2}T_{2}} \tag{6.4.2} \)
In many of these problems one considers the changes in a sample of gas where the number of moles does not change. In such a case one can write the relationship as
\( \dfrac{P_{1}V_{1}}{T_{1}}= \dfrac{P_{2}V_{2}}{T_{2}} \tag{6.4.3} \)
If two of the parameters specifying the thermodynamic state of the gas sample are held constant, one recovers simple proportional relationships among the other two which were experimentally observed centuries ago by
Robert Boyle
\( V \propto \dfrac{1}{P} \left ( at \;constant\; n,\; V \right ) \tag{6.4.4} \)
expresses the idea that at constant composition (e.g. the number of moles of gas) and temperature the product PV is a constant.
Jacques Charles and Joseph-Louis Gay-Lussac
\( V \propto T \left (at \;constant\; n, P \right ) \tag{6.4.5} \)
expresses the idea that at constant composition (e.g. the number of moles of gas) and pressure the ratio V/T is a constant. Using Boyle's law this also can be written as P/T being constant
Amedeo Avogadro
\( V \propto n \left (at \;constant\; T, P \right ) \tag{6.4.6} \)
In its original formulation, Avogadro's law stated that equal volumes of gas at constant temperature and pressure held the same number of molecules
Brief descriptions of these scientists work are found at the end of this section.
Example 6.4.1
Charles originally observed the change of volume with temperature in balloon ascents and descents that he made. Suppose that Charles had changed his plans and carried out his initial flight not in August but on a cold day in January, when the temperature at ground level was −10°C. How large a balloon would he have needed to contain the same amount of hydrogen gas at the same pressure as in Example 5?
Given: temperature, pressure, amount, and volume in August; temperature in January
Asked for: volume in January
Strategy:
A Use the results from Example 5 for August as the initial conditions and then calculate the change in volume due to the change in temperature from 86°F to 14°F. Begin by constructing a table showing the initial and final conditions.
B Rearrange the ideal gas law to isolate those quantities that differ between the initial and final states on one side of the equation, in this case V and T.
C Equate the ratios of those terms that change for the two sets of conditions. Making sure to use the appropriate units, insert the quantities and solve for the unknown parameter.
Solution:
A To see exactly which parameters have changed and which are constant, prepare a table of the initial and final conditions:
| August (initial) | January (final) | |
|---|---|---|
| T | 30°C = 303 K | −10°C = 263 K |
| P | 0.980 atm | 0.980 atm |
| n | 1.23 × 103 mol H2 | 1.23 × 103 mol H2 |
| V | 31,150 L | ? |
Thus we are asked to calculate the effect of a change in temperature on the volume of a fixed amount of gas at constant pressure.
B Both \(n\) and \(P\) are the same in both cases (\(n_i=n_f,P_i=P_f\)). Therefore, Equation 6.4.3 can be simplified to:
\[\dfrac{V_i}{T_i}=\dfrac{V_f}{T_f}\]
This is the relationship first noted by Charles.
C Solving the equation for \(V_f\), we get:
\[V_f=V_i\times\dfrac{T_f}{T_i}=\rm31150\;L\times\dfrac{263\;K}{303\;K}=2.70\times10^4\;L\]
It is important to check your answer to be sure that it makes sense, just in case you have accidentally inverted a quantity or multiplied rather than divided. In this case, the temperature of the gas decreases. Because we know that gas volume decreases with decreasing temperature, the final volume must be less than the initial volume, so the answer makes sense. We could have calculated the new volume by plugging all the given numbers into the ideal gas law, but it is generally much easier and faster to focus on only the quantities that change.
It is important to check your answer to be sure that it makes sense, just in case you have accidentally inverted a quantity or multiplied rather than divided. In this case, the temperature of the gas decreases. Because we know that gas volume decreases with decreasing temperature, the final volume must be less than the initial volume, so the answer makes sense. We could have calculated the new volume by plugging all the given numbers into the ideal gas law, but it is generally much easier and faster to focus on only the quantities that change.
Exercise
At a laboratory party, a helium-filled balloon with a volume of 2.00 L at 22°C is dropped into a large container of liquid nitrogen (T = −196°C). What is the final volume of the gas in the balloon?
Answer: 0.52 L
Example 8 illustrates the relationship originally observed by Charles. We could work through similar examples illustrating the inverse relationship between pressure and volume noted by Boyle (PV = constant) and the relationship between volume and amount observed by Avogadro (V/n = constant). We will not do so for all cases, however, because it is more important to note that the historically important gas laws are only special cases of the ideal gas law in which two quantities are varied while the other two remain fixed. The method used in Example 8 can be applied in any such case, as we demonstrate in Example 9 (which also shows why heating a closed container of a gas, such as a butane lighter cartridge or an aerosol can, may cause an explosion).
Example 6.4.2
Aerosol cans are prominently labeled with a warning such as “Do not incinerate this container when empty.” Assume that you did not notice this warning and tossed the “empty” aerosol can in Exercise 5 (0.025 mol in 0.406 L, initially at 25°C and 1.5 atm internal pressure) into a fire at 750°C. What would be the pressure inside the can (if it did not explode)?
Given: initial volume, amount, temperature, and pressure; final temperature
Asked for: final pressure
Strategy:
Follow the strategy outlined in Example 8.
Solution:
Prepare a table to determine which parameters change and which are held constant:
| Initial | Final | |
|---|---|---|
| V | 0.406 L | 0.406 L |
| n | 0.025 mol | 0.025 mol |
| T | 25°C = 298 K | 750°C = 1023 K |
| P | 1.5 atm | ? |
Once again, two parameters are constant while one is varied, and we are asked to calculate the fourth. As before, we begin with the ideal gas law and rearrange it as necessary to get all the constant quantities on one side. In this case, because V and n are constant, we rearrange to obtain
\( P=\left ( \dfrac{nR}{V} \right )\left ( T \right )= constant \times T \)
Dividing both sides by T, we obtain an equation analogous to the one in Example 6, P/T = nR/V = constant. Thus the ratio of P to T does not change if the amount and volume of a gas are held constant. We can thus write the relationship between any two sets of values of P and T for the same sample of gas at the same volume as
\( \dfrac{P_{i}}{T_{i}}=\dfrac{P_{f}}{T_{f}} \)
In this example, Pi = 1.5 atm, Ti = 298 K, and Tf = 1023 K, and we are asked to find Pf. Solving for Pf and substituting the appropriate values, we obtain
\[P_f=P_i\times\dfrac{T_f}{T_i}=\rm1.5\;atm\times\dfrac{1023\;K}{298\;K}=5.1\;atm\]
This pressure is more than enough to rupture a thin sheet metal container and cause an explosion!
Exercise
Suppose that a fire extinguisher, filled with CO2 to a pressure of 20.0 atm at 21°C at the factory, is accidentally left in the sun in a closed automobile in Tucson, Arizona, in July. The interior temperature of the car rises to 160°F (71.1°C). What is the internal pressure in the fire extinguisher?
Answer: 23.4 atm
Example 6.4.3
We saw in Example 5 that Charles used a balloon with a volume of 31,150 L for his initial ascent and that the balloon contained 1.23 × 103 mol of H2 gas initially at 30°C and 745 Torr. Suppose that Gay-Lussac had also used this balloon for his record-breaking ascent to 23,000 ft and that the pressure and temperature at that altitude were 312 Torr and −30°C, respectively. To what volume would the balloon have had to expand to hold the same amount of hydrogen gas at the higher altitude?
Given: initial pressure, temperature, amount, and volume; final pressure and temperature
Asked for: final volume
Strategy:
Follow the strategy outlined in Example 6.
Solution:
Begin by setting up a table of the two sets of conditions:
| Initial | Final | |
|---|---|---|
| P | 745 Torr = 0.980 atm | 312 Torr = 0.411 atm |
| T | 30°C = 303 K | −30°C = 243 K |
| n | 1.23 × 103 mol H2 | 1.23 × 103 mol H2 |
| V | 31,150 L | ? |
Thus all the quantities except V2 are known. Solving Equation 6.4.3 for V2 and substituting the appropriate values give
\[V_f=V_i\times\dfrac{P_i}{P_f}\dfrac{T_f}{T_i}=\rm3.115\times10^4\;L\times\dfrac{0.980\; \cancel{atm}}{0.411\;\cancel{atm}}\dfrac{243\;\cancel{K}}{303\;\cancel{K}}=5.96\times10^4\;L\]
Does this answer make sense? Two opposing factors are at work in this problem: decreasing the pressure tends to increase the volume of the gas, while decreasing the temperature tends to decrease the volume of the gas. Which do we expect to predominate? The pressure drops by more than a factor of two, while the absolute temperature drops by only about 20%. Because the volume of a gas sample is directly proportional to both T and 1/P, the variable that changes the most will have the greatest effect on V. In this case, the effect of decreasing pressure predominates, and we expect the volume of the gas to increase, as we found in our calculation.
We could also have solved this problem by solving the ideal gas law for V and then substituting the relevant parameters for an altitude of 23,000 ft:
\( V=\dfrac{nRT}{P}= \dfrac{\left ( 1.23\times 10^{3}\; \cancel{mol}\left [ 0.082057 \; \left ( L\cdot \cancel{atm} \right )/\left ( \cancel{K} \cdot \cancel{mol} \right ) \right ]\left ( 243 \; \cancel{K} \right ) \right )}{0.411 \; \cancel{atm}} = 5.97\times 10^{4} L \)
Except for a difference caused by rounding to the last significant figure, this is the same result we obtained previously. There is often more than one “right” way to solve chemical problems.
Exercise
A steel cylinder of compressed argon with a volume of 0.400 L was filled to a pressure of 145 atm at 10°C. At 1.00 atm pressure and 25°C, how many 15.0 mL incandescent light bulbs could be filled from this cylinder? (Hint: find the number of moles of argon in each container.)
Answer: 4.07 × 103
The Relationship between Pressure and Volume
As the pressure on a gas increases, the volume of the gas decreases because the gas particles are forced closer together. Conversely, as the pressure on a gas decreases, the gas volume increases because the gas particles can now move farther apart. Weather balloons get larger as they rise through the atmosphere to regions of lower pressure because the volume of the gas has increased; that is, the atmospheric gas exerts less pressure on the surface of the balloon, so the interior gas expands until the internal and external pressures are equal.
Robert Boyle (1627–1691)
Boyle, the youngest (and 14th!) child of the Earl of Cork, was an important early figure in chemistry whose views were often at odds with accepted wisdom. Boyle’s studies of gases are reported to have utilized a very tall J-tube that he set up in the entryway of his house, which was several stories tall. He is known for the gas law that bears his name and for his book, The Sceptical Chymist, which was published in 1661 and influenced chemists for many years after his death. In addition, one of Boyle’s early essays on morals is said to have inspired Jonathan Swift to write Gulliver’s Travels.
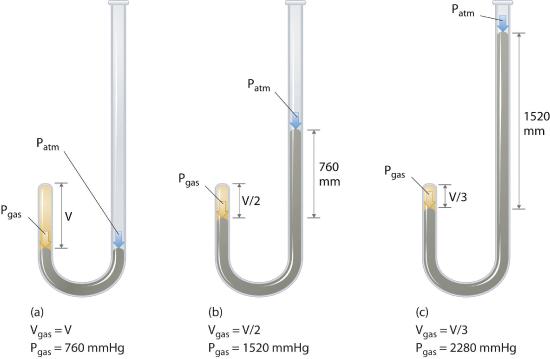
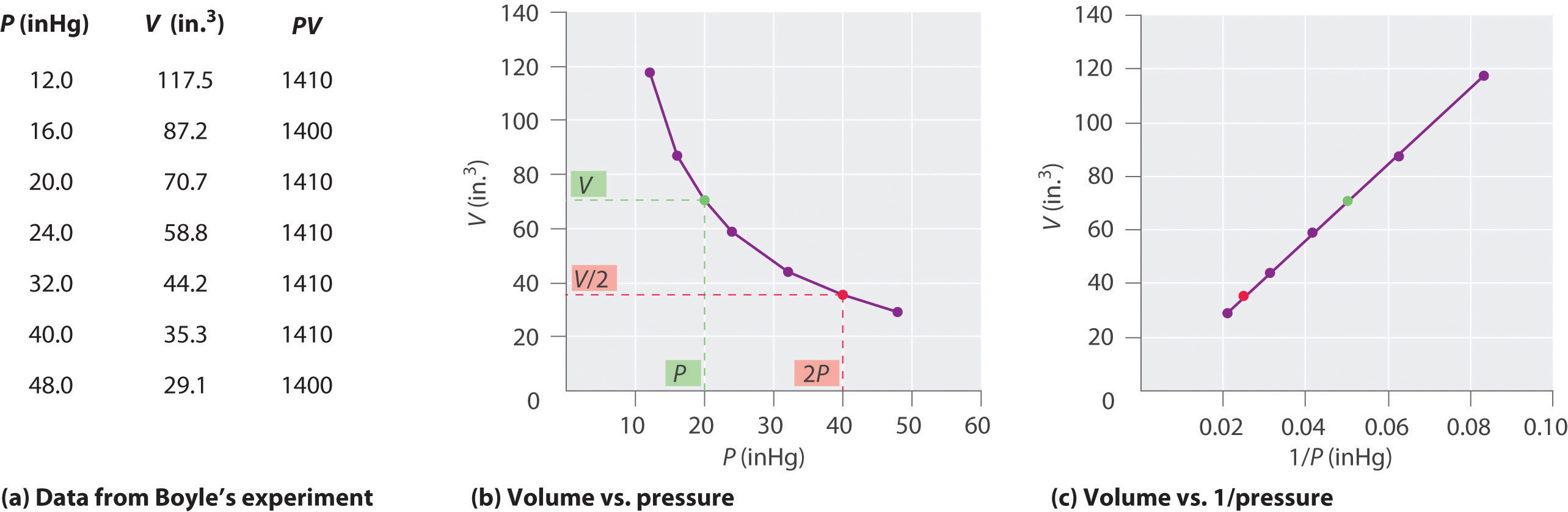
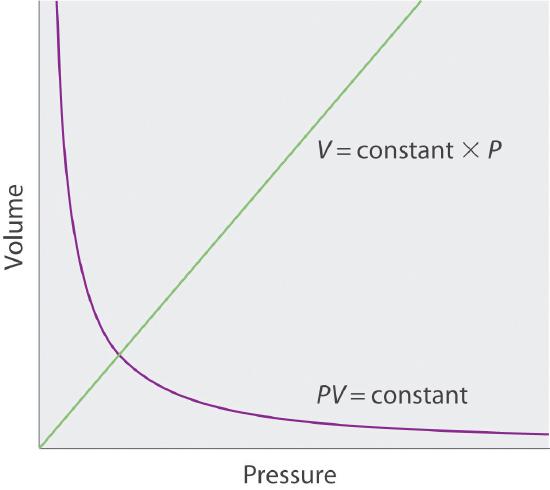
The Irish chemist Robert Boyle (1627–1691) carried out some of the earliest experiments that determined the quantitative relationship between the pressure and the volume of a gas. Boyle used a J-shaped tube partially filled with mercury, as shown in Figure 6.4.1. In these experiments, a small amount of a gas or air is trapped above the mercury column, and its volume is measured at atmospheric pressure and constant temperature. More mercury is then poured into the open arm to increase the pressure on the gas sample. The pressure on the gas is atmospheric pressure plus the difference in the heights of the mercury columns, and the resulting volume is measured. This process is repeated until either there is no more room in the open arm or the volume of the gas is too small to be measured accurately. Data such as those from one of Boyle’s own experiments may be plotted in several ways (Figure 6.4.2 ). A simple plot of V versus P gives a curve called a hyperbola and reveals an inverse relationship between pressure and volume: as the pressure is doubled, the volume decreases by a factor of two. This relationship between the two quantities is described as follows:
\( PV = constant \tag{6.4.7} \)
Figure 6.4.1 Boyle’s Experiment Using a J-Shaped Tube to Determine the Relationship between Gas Pressure and Volume (a) Initially the gas is at a pressure of 1 atm = 760 Torr (the mercury is at the same height in both the arm containing the sample and the arm open to the atmosphere); its volume is V. (b) If enough mercury is added to the right side to give a difference in height of 760 Torr between the two arms, the pressure of the gas is 760 mmHg (atmospheric pressure) + 760 mmHg = 1520 mmHg and the volume is V/2. (c) If an additional 760 Torr is added to the column on the right, the total pressure on the gas increases to 2280 Torr, and the volume of the gas decreases to V/3.
Figure6.4.2 Plots of Boyle’s Data (a) Here are actual data from a typical experiment conducted by Boyle. Boyle used non-SI units to measure the volume (in.3 rather than cm3) and the pressure (in. Hg rather than Torr). (b) This plot of pressure versus volume is a hyperbola. Because PV is a constant, decreasing the pressure by a factor of two results in a twofold increase in volume and vice versa. (c) A plot of volume versus 1/pressure for the same data shows the inverse linear relationship between the two quantities, as expressed by the equation V = constant/P.
Dividing both sides by P gives an equation illustrating the inverse relationship between P and V:
\( V=\dfrac{constant}{P}=constant\left ( \dfrac{1}{P} \right )\; or\; V \propto \dfrac{1}{P} \tag{6.4.8}\)
where the ∝ symbol is read “is proportional to.” A plot of V versus 1/P is thus a straight line whose slope is equal to the constant in Equation 6.4.7. Dividing both sides of Equation 6.4.7 by V instead of P gives a similar relationship between P and 1/V. The numerical value of the constant depends on the amount of gas used in the experiment and on the temperature at which the experiments are carried out. This relationship between pressure and volume is known as Boyle’s lawA law that states that at constant temperature, the volume of a fixed amount of a gas is inversely proportional to its pressure., after its discoverer, and can be stated as follows: At constant temperature, the volume of a fixed amount of a gas is inversely proportional to its pressure.
The Relationship between Temperature and Volume
Hot air rises, which is why hot-air balloons ascend through the atmosphere and why warm air collects near the ceiling and cooler air collects at ground level. Because of this behavior, heating registers are placed on or near the floor, and vents for air-conditioning are placed on or near the ceiling. The fundamental reason for this behavior is that gases expand when they are heated. Because the same amount of substance now occupies a greater volume, hot air is less dense than cold air. The substance with the lower density—in this case hot air—rises through the substance with the higher density, the cooler air.
The first experiments to quantify the relationship between the temperature and the volume of a gas were carried out in 1783 by an avid balloonist, the French chemist Jacques Alexandre César Charles (1746–1823). Charles’s initial experiments showed that a plot of the volume of a given sample of gas versus temperature (in degrees Celsius) at constant pressure is a straight line. Similar but more precise studies were carried out by another balloon enthusiast, the Frenchman Joseph-Louis Gay-Lussac (1778–1850), who showed that a plot of V versus T was a straight line that could be extrapolated to a point at zero volume, a theoretical condition now known to correspond to −273.15°C (Figure 9.3.1 ) or absolute zero. A sample of a real gas cannot really have a volume of zero because any sample of matter must have some volume. Furthermore, at 1 atm pressure all gases liquefy at temperatures well above −273.15°C. However, the ideal gas model does allow for reaching absolute zero, but the second law of thermodynamics, which will be discussed in Unit 7, makes this impossible.
Jacques Alexandre César Charles (1746–1823) and Joseph-Louis Gay-Lussac (1778–1850)
In 1783, Charles filled a balloon (“aerostatic globe”) with hydrogen (generated by the reaction of iron with more than 200 kg of acid over several days) and flew successfully for almost an hour. When the balloon descended in a nearby village, however, the terrified townspeople destroyed it. In 1804, Gay-Lussac managed to ascend to 23,000 ft (more than 7000 m) to collect samples of the atmosphere to analyze its composition as a function of altitude. In the process, he had trouble breathing and nearly froze to death, but he set an altitude record that endured for decades. (To put Gay-Lussac’s achievement in perspective, recall that modern jetliners cruise at only 35,000 ft!)
We can state Charles’s and Gay-Lussac’s findings in simple terms: At constant pressure, the volume of a fixed amount of gas is directly proportional to its absolute temperature (in Kelvin). This relationship is often referred to as Charles’s law
Charles’s law is valid for virtually all gases at temperatures well above their boiling points. Note that the temperature must be expressed in kelvins, not in degrees Celsius.
The Relationship between Amount and Volume
We can demonstrate the relationship between the volume and the amount of a gas by filling a balloon; as we add more gas, the balloon gets larger. The specific quantitative relationship was discovered by the Italian chemist Amedeo Avogadro, who recognized the importance of Gay-Lussac’s work on combining volumes of gases. In 1811, Avogadro postulated that, at the same temperature and pressure, equal volumes of gases contain the same number of gaseous particles. (This is the historic “Avogadro’s hypothesis” introduced in Chapter 1 .) A logical corollary, sometimes called Avogadro’s lawA law that states that at constant temperature and pressure, the volume of a sample of gas is directly proportional to the number of moles of gas in the sample., describes the relationship between the volume and the amount of a gas: At constant temperature and pressure, the volume of a sample of gas is directly proportional to the number of moles of gas in the sample. Stated mathematically,
\( V=\left ( constant \right )\left (n \right )or\; V \propto n \left ( at \;constant \;T \;and \;P \right )\tag{6.3.4} \)
This relationship is valid for most gases at relatively low pressures, but deviations from strict linearity are observed at elevated pressures.
Summary
Boyle showed that the volume of a sample of a gas is inversely proportional to its pressure (Boyle’s law), Charles and Gay-Lussac demonstrated that the volume of a gas is directly proportional to its temperature (in kelvins) at constant pressure (Charles’s law), and Avogadro postulated that the volume of a gas is directly proportional to the number of moles of gas present (Avogadro’s law). Plots of the volume of gases versus temperature extrapolate to zero volume at −273.15°C, which is absolute zero (0 K), the lowest temperature possible. Charles’s law implies that the volume of a gas is directly proportional to its absolute temperature.
Key Takeaway
- The volume of a gas is inversely proportional to its pressure and directly proportional to its temperature and the amount of gas.
Conceptual Problems
-
Sketch a graph of the volume of a gas versus the pressure on the gas. What would the graph of V versus P look like if volume was directly proportional to pressure?
-
What properties of a gas are described by Boyle’s law, Charles’s law, and Avogadro’s law? In each law, what quantities are held constant? Why does the constant in Boyle’s law depend on the amount of gas used and the temperature at which the experiments are carried out?
-
Use Charles’s law to explain why cooler air sinks.
4. Use Boyle’s law to explain why it is dangerous to heat even a small quantity of water in a sealed container.
For an ideal gas, is volume directly proportional or inversely proportional to temperature? What is the volume of an ideal gas at absolute zero?
For a given amount of a gas, the volume, temperature, and pressure under any one set of conditions are related to the volume, the temperature, and the pressure under any other set of conditions by the equation
\( \dfrac{P_{1}V_{1}}{T_{1}}= \dfrac{P_{2}V_{2}}{T_{2}} \)
Derive this equation from the ideal gas law. At constant temperature, this equation reduces to one of the laws discussed in Section 6.3; which one? At constant pressure, this equation reduces to one of the laws discussed in Section 6.3; which one?
Predict the effect of each change on one variable if the other variables are held constant.
- If the number of moles of gas increases, what is the effect on the temperature of the gas?
- If the temperature of a gas decreases, what is the effect on the pressure of the gas?
- If the volume of a gas increases, what is the effect on the temperature of the gas?
- If the pressure of a gas increases, what is the effect on the number of moles of the gas?
What would the ideal gas law be if the following were true?
- volume were proportional to pressure
- temperature were proportional to amount
- pressure were inversely proportional to temperature
- volume were inversely proportional to temperature
- both pressure and volume were inversely proportional to temperature
Given the following initial and final values, what additional information is needed to solve the problem using the ideal gas law?
| Given | Solve for |
|---|---|
| V1, T1, T2, n1 | n 2 |
| P1, P2, T2, n2 | n 1 |
| T1, T2 | V 2 |
| P1, n1 | P 2 |
Given the following information and using the ideal gas law, what equation would you use to solve the problem?
| Given | Solve for |
|---|---|
| P1, P2, T1 | T 2 |
| V1, n1, n2 | V 2 |
| T1, T2, V1, V2, n2 | n 1 |
Using the ideal gas law as a starting point, derive the relationship between the density of a gas and its molar mass. Which would you expect to be denser—nitrogen or oxygen? Why does radon gas accumulate in basements and mine shafts?
Use the ideal gas law to derive an equation that relates the remaining variables for a sample of an ideal gas if the following are held constant.
- amount and volume
- pressure and amount
- temperature and volume
- temperature and amount
- pressure and temperature
Tennis balls that are made for Denver, Colorado, feel soft and do not bounce well at lower altitudes. Use the ideal gas law to explain this observation. Will a tennis ball designed to be used at sea level be harder or softer and bounce better or worse at higher altitudes?
Answer
Numerical Problems
-
A 1.00 mol sample of gas at 25°C and 1.0 atm has an initial volume of 22.4 L. Calculate the results of each change, assuming all the other conditions remain constant.
- The pressure is changed to 85.7 Torr. How many milliliters does the gas occupy?
- The volume is reduced to 275 mL. What is the pressure in millimeters of mercury?
- The pressure is increased to 25.3 atm. What is the temperature in degrees Celsius?
- The sample is heated to 30°C. What is the volume in liters?
- The sample is compressed to 1255 mL, and the pressure is increased to 2555 torr. What is the temperature of the gas in kelvins?
-
A 1.00 mol sample of gas is at 300 K and 4.11 atm. What is the volume of the gas under these conditions? The sample is compressed to 6.0 atm at constant temperature, giving a volume of 3.99 L. Is this result consistent with Boyle’s law?
- m
A 8.60 L tank of nitrogen gas at a pressure of 455 Torr is connected to an empty tank with a volume of 5.35 L. What is the final pressure in the system after the valve connecting the two tanks is opened? Assume that the temperature is constant.
At constant temperature, what pressure in atmospheres is needed to compress 14.2 L of gas initially at 25.2 atm to a volume of 12.4 L? What pressure is needed to compress 27.8 L of gas to 20.6 L under similar conditions?
One method for preparing hydrogen gas is to pass HCl gas over hot aluminum; the other product of the reaction is AlCl3. If you wanted to use this reaction to fill a balloon with a volume of 28,500 L at sea level and a temperature of 78°F, what mass of aluminum would you need? What volume of HCl at STP would you need?
An 3.50 g sample of acetylene is burned in excess oxygen according to the following reaction:
2 C2H2(g) + 5 O2(g) → 4 CO2(g) + 2 H2O(l)At STP, what volume of CO2(g) is produced?
Calculate the density of ethylene (C2H4) under each set of conditions.
- 7.8 g at 0.89 atm and 26°C
- 6.3 mol at 102.6 kPa and 38°C
- 9.8 g at 3.1 atm and −45°C
Determine the density of O2 under each set of conditions.
- 42 g at 1.1 atm and 25°C
- 0.87 mol at 820 Torr and 45°C
- 16.7 g at 2.4 atm and 67°C
At 140°C, the pressure of a diatomic gas in a 3.0 L flask is 635 kPa. The mass of the gas is 88.7 g. What is the most likely identity of the gas?
What volume must a balloon have to hold 6.20 kg of H2 for an ascent from sea level to an elevation of 20,320 ft, where the temperature is −37°C and the pressure is 369 Torr?
What must be the volume of a balloon that can hold 313.0 g of helium gas and ascend from sea level to an elevation of 1.5 km, where the temperature is 10.0°C and the pressure is 635.4 Torr?
A typical automobile tire is inflated to a pressure of 28.0 lb/in. Assume that the tire is inflated when the air temperature is 20°C; the car is then driven at high speeds, which increases the temperature of the tire to 43°C. What is the pressure in the tire? If the volume of the tire had increased by 8% at the higher temperature, what would the pressure be?
The average respiratory rate for adult humans is 20 breaths per minute. If each breath has a volume of 310 mL of air at 20°C and 0.997 atm, how many moles of air does a person inhale each day? If the density of air is 1.19 kg/m3, what is the average molecular mass of air?
Kerosene has a self-ignition temperature of 255°C. It is a common accelerant used by arsonists, but its presence is easily detected in fire debris by a variety of methods. If a 1.0 L glass bottle containing a mixture of air and kerosene vapor at an initial pressure of 1 atm and an initial temperature of 23°C is pressurized, at what pressure would the kerosene vapor ignite?
Answer
-
- 1.99 × 105 mL
- 6.19 × 104 Torr
- 7270°C
- 22.8 L
- 51.4 K
-
Contributors
- Anonymous
- Modified by Joshua Halpern, Scott Sinex and Scott Johnson
- Thumbnail from Wikimedia