Chapter 4.8: Metallic Bonding
- Page ID
- 19896
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\) |
Prince George's Community College |
 |
| Unit I: Atoms Unit II: Molecules Unit III: States of Matter Unit IV: Reactions Unit V: Kinetics & Equilibrium Unit VI: Thermo & Electrochemistry Unit VII: Nuclear Chemistry |
||
Learning Objectives
- To learn about metallic bonding.
Metals have several qualities that are unique, such as the ability to conduct electricity, a low ionization energy, and a low electronegativity (so they will give up electrons easily, i.e., they are cations). Their physical properties include a lustrous (shiny) appearance, and they are malleable and ductile. Metals have a crystal structure.
- Metals that are malleable can be beaten into thin sheets, for example: aluminum foil.
- Metals that are ductile can be drawn into wires, for example: copper wire.
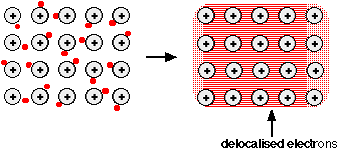
In the 1900's, Paul Drüde came up with the sea of electrons theory by modeling metals as a mixture of atomic cores (atomic cores = positive nuclei + inner shell of electrons) and valence electrons. In this model, the valence electrons are free, delocalized, mobile, and not associated with any particular atom. For example: metallic cations surrounded by a "sea" of electrons. This model assumes that the valence electrons do not interact with each other. This model may account for:
- Malleability and Ductility: The sea of electrons surrounding the protons act like a cushion, and so when the metal is hammered on, for instance, the over all composition of the structure of the metal is not harmed or changed. The protons may be rearranged but the sea of electrons with adjust to the new formation of protons and keep the metal intact.
- Heat capacity: This is explained by the ability of free electrons to move about the solid conducting heat
- Luster: The free electrons can absorb photons in the "sea," so metals are opaque-looking. Electrons on the surface can bounce back light at the same frequency that the light hits the surface, therefore the metal appears to be shiny.
- Conductivity: Since the electrons are free, if electrons from an outside source were pushed into a metal wire at one end, the electrons would be pushed into the the wire and come out at the other end at the same rate (conductivity is the movement of charge).
Amazingly, Drude's electron sea model predates Rutherford's nuclear model of the atom and Lewis' octet rule. It is, however, a useful qualitative model of metallic bonding even to this day. As it did for Lewis' octet rule, the quantum revolution of the 1930s told us about the underlying chemistry. Drude's electron sea model assumed that valence electrons were free to move in metals, quantum mechanical calculations told us why this happened.
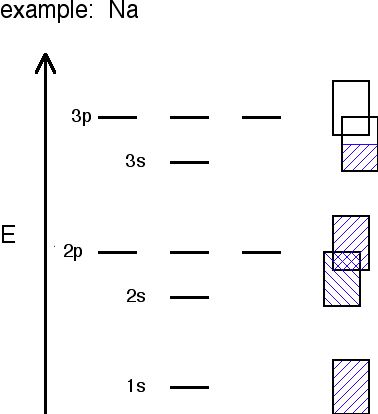
Metallic bonding in sodium
Metals tend to have high melting points and boiling points suggesting strong bonds between the atoms. Even a metal like sodium (melting point 97.8°C) melts at a considerably higher temperature than the element (neon) which precedes it in the Periodic Table.
Sodium has the electronic structure 1s22s22p63s1. When sodium atoms come together, the electron in the 3s atomic orbital of one sodium atom shares space with the corresponding electron on a neighboring atom to form a molecular orbital - in much the same sort of way that a covalent bond is formed.
The difference, however, is that each sodium atom is being touched by eight other sodium atoms - and the sharing occurs between the central atom and the 3s orbitals on all of the eight other atoms. And each of these eight is in turn being touched by eight sodium atoms, which in turn are touched by eight atoms - and so on and so on, until you have taken in all the atoms in that lump of sodium.
All of the 3s orbitals on all of the atoms overlap to give a vast number of molecular orbitals which extend over the whole piece of metal. There have to be huge numbers of molecular orbitals, of course, because any orbital can only hold two electrons.
The electrons can move freely within these molecular orbitals, and so each electron becomes detached from its parent atom. The electrons are said to be delocalized. The metal is held together by the strong forces of attraction between the positive nuclei and the delocalized electrons.
This is sometimes described as "an array of positive ions in a sea of electrons".
Each positive center in the diagram represents all the rest of the atom apart from the outer electron, but that electron hasn't been lost - it may no longer have an attachment to a particular atom, but those electrons are still there in the structure. Sodium metal is therefore written as Na - not Na+.
Metallic bonding in magnesium
If you work through the same argument with magnesium, you end up with stronger bonds and so a higher melting point./p>
Magnesium has the outer electronic structure 3s2. Both of these electrons become delocalised, so the "sea" has twice the electron density as it does in sodium. The remaining "ions" also have twice the charge (if you are going to use this particular view of the metal bond) and so there will be more attraction between "ions" and "sea".
More realistically, each magnesium atom has 12 protons in the nucleus compared with sodium's 11. In both cases, the nucleus is screened from the delocalised electrons by the same number of inner electrons - the 10 electrons in the 1s2 2s2 2p6 orbitals.
That means that there will be a net pull from the magnesium nucleus of 2+, but only 1+ from the sodium nucleus.
So not only will there be a greater number of delocalized electrons in magnesium, but there will also be a greater attraction for them from the magnesium nuclei. Magnesium atoms also have a slightly smaller radius than sodium atoms, and so the delocalised electrons are closer to the nuclei. Each magnesium atom also has twelve near neighbors rather than sodium's eight. Both of these factors increase the strength of the bond still further.
Metallic bonding in transition elements
Transition metals tend to have particularly high melting points and boiling points. The reason is that they can involve the 3d electrons in the delocalization as well as the 4s. The more electrons you can involve, the stronger the attractions tend to be.
The strength of a metallic bond depends on three things:
- The number of electrons that become delocalized from the metal ions
- The charge of the cation (metal).
- The size of the cation.
A strong metallic bond will be the result of more delocalized electrons, which causes the effective nuclear charge on electrons on the cation to increase, in effect making the size of the cation smaller. Metallic bonds are strong and require a great deal of energy to break, and therefore metals have high melting and boiling points.
A metallic bonding theory must explain how so much bonding can occur with such few electrons (since metals are located on the left side of the periodic table and do not have many electrons in their valence shells). The theory must also account for all of a metal's unique chemical and physical properties.
Band Theory
Band Theory was developed with some help from the knowledge gained during the quantum revolution in science. In 1928, Felix Bloch had the idea to take the quantum theory and apply it to solids. In 1927, Walter Heitler and Fritz London explained how these many levels can combine together to form bands- orbitals so close together in energy that they are continuous
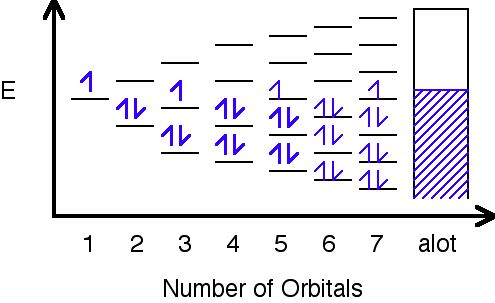
In this image, orbitals are represented by the black horizontal lines, and they are being filled with an increasing number of electrons as their amount increases. Eventually, as more orbitals are added, the space in between them decreases to hardly anything, and as a result, a band is formed where the orbitals have been filled.
Different metals will produce different combinations of filled and half filled bands.
Sodium's bands are shown with the rectangles. Filled bands are colored in blue. As you can see, bands may overlap each other (the bands are shown askew to be able to tell the difference between different bands). The lowest unoccupied band is called the conduction band, and the highest occupied band is called the valence band.
The probability of finding an electron in the conduction band is shown by the equation:
\[ P= \dfrac{1}{e^{ \Delta E/RT}+1} \]
The ∆E in the equation stands for the change in energy or energy gap. t stands for the temperature, and R is a bonding constant. That equation and this table below show how the bigger difference in energy is, or gap, between the valence band and the conduction band, the less likely electrons are to be found in the conduction band. This is because they cannot be excited enough to make the jump up to the conduction band.
| ELEMENT | ∆E(kJ/mol) of energy gap | # of electrons/cm^3 in conduction band @ 300K | insulator, or conductor? |
| C (diamond) | 524 (big band gap) | 10-27 | insulator |
| Si | 117 (smaller band gap, but not a full conductor) | 109 | semiconductor |
| Ge | 66 (smaller band gap, but still not a full conductor) | 1013 | semiconductor |
Conductors, Insulators and Semiconductors
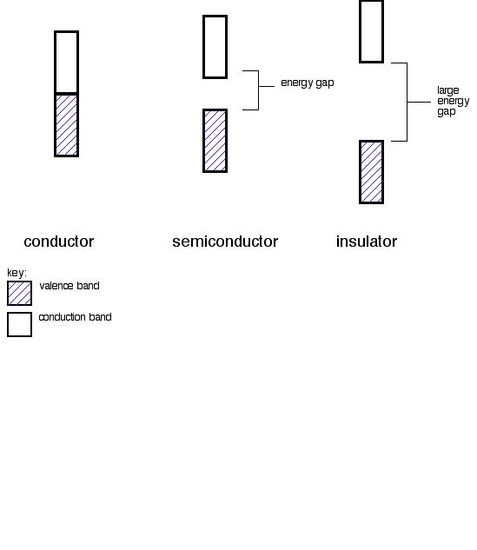
A. Conductors
Metals are conductors. There is no band gap between their valence and conduction bands, since they overlap. There is a continuous availability of electrons in these closely spaced orbitals.
B. Insulators
In insulators, the band gap between the valence band the the conduction band is so large that electrons cannot make the energy jump from the valence band to the conduction band.
C. Semiconductors
Semiconductors have a small energy gap between the valence band and the conduction band. Electrons can make the jump up to the conduction band, but not with the same ease as they do in conductors.
Outside Links
- http://www.youtube.com/watch?v=HWRHT...87AF6948F5E8F9 (start at 9 minutes)
- http://www.youtube.com/watch?v=qK6DgAM-q7U (start at 13 minutes)
- http://en.wikipedia.org/wiki/Metallic_bonding
- Metallic Bonding: http://www.youtube.com/watch?v=CGA8sRwqIFg&feature=youtube_gdata
Problems
- How do you distinguish between a valence band and a conduction band?
- Is the energy gap between an insulator smaller or larger than the energy gap between a semiconductor?
- What two methods bring conductivity to semiconductors?
- You are more likely to find electrons in a conduction band if the energy gap is smaller/larger? 5. The property of being able to be drawn into a wire is called...
Answers
- The valence band is the highest band with electrons in it, and the conduction band is the highest band with no electrons in it.
- Larger
- Electron transport and hole transport
- Smaller
- Ductility
References
- Petrucci, Harwood, Herring, Madura. GENERAL CHEMISTRY Principles and Modern Applications 9th Edition. Macmillan Publishing Co: New Jersey. 1989.
- Moore, John T. Chemistry Made Simple. Random House Inc: New York. 2004.
Contributors
- Sierra Blair (UCD)
- Modified by Joshua Halpern, Scott Sinex and Scott Johnson (minor)
Jim Clark (Chemguide.co.uk)