Chapter 3.2: Energetics of Ion Formation
- Page ID
- 19883
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\) |
Prince George's Community College |
 |
| Unit I: Atoms Unit II: Molecules Unit III: States of Matter Unit IV: Reactions Unit V: Kinetics & Equilibrium Unit VI: Thermo & Electrochemistry Unit VII: Nuclear Chemistry |
||
Learning Objectives
- To correlate ionization energies, electron affinities, and electronegativities with the chemistry of the elements.
We have seen that when elements react, they often gain or lose enough electrons to achieve the valence electron configuration of the nearest noble gas. In this section, we develop a more quantitative approach to predicting such reactions by examining periodic trends in the energy changes that accompany ion formation.
Ionization Energies
Because atoms do not spontaneously lose electrons, energy is required to remove an electron from an atom to form a cation. Chemists define the ionization energy (\(I\)) (The minimum amount of energy needed to remove an electron from the gaseous atom in its ground state: \(E_{(g)}+ I \rightarrow E^++e^-\)) of an element as the amount of energy needed to remove an electron from the gaseous atom \(E\) in its ground state. \(I\) is therefore the energy required for the reaction
\( E\left ( g \right )+I\rightarrow E\left ( g \right )^{+}+e^{-} \; \; \; \; energy\; required=I \tag{3.2.1} \)
because an input of energy is required, the ionization energy is always positive (\(I > 0\)) for the reaction as written in Equation 3.2.1. Larger values of \(I\) mean that the electron is more tightly bound to the atom and harder to remove. Typical units for ionization energies are kilojoules/mole (kJ/mol) or electron volts (eV):
1 eV/atom = 96.49 kJ/mol
An electron volt is the appropriate unit to describe the energy needed to remove an electron from one atom. kJ/mole is the energy needed to ionize a mole of atoms.
If an atom possesses more than one electron, the amount of energy needed to remove successive electrons increases steadily. We can define a first ionization energy (\(I_1\)), a second ionization energy (\(I_2\)), and in general an \(n^{th}\) ionization energy (\(I_n\)) according to the following reactions:
- \( I_{1} = First\; Ionization\; energy \; \; \; \; E \left ( g \right ) + I_{1} \rightarrow E \left (g \right )^{+}+e^{-} \; \; \; \; \tag{3.2.2} \)
- \( I_{2} = Second\; Ionization\; energy \; \; \; \; E \left ( g \right )^{+} + I_{2} \rightarrow E \left ( g \right )^{2+}+e^{-}\; \; \; \; \tag{3.2.3} \)
- \( I_{n} = nth\; Ionization\; energy \; \; \; \; E \left ( g \right )^{\left ( n-1 \right )+} + I_{n} \rightarrow E \left ( g \right )^{n+}+e^{-} \; \; \; \; \tag{3.2.4} \)
- First, the second electron is being removed from a positively charged species rather than a neutral one, so in accordance with Coulomb’s law, more energy is required.
- Second, removing the first electron reduces the repulsive forces among the remaining electrons, so the attraction of the remaining electrons to the nucleus is stronger.
Note the Pattern
Successive ionization energies for an element increase steadily.
Table 3.2.1 Ionization Energies (in kJ/mol) for Removing Successive Electrons from Li and Be
| Reaction | I | Reaction | I |
|---|---|---|---|
|
\( \begin{array}{lcl} Li\left ( g \right ) & \rightarrow & Li^{+}+e^{-} \\ _{1s^{2}2s^{1}} & = & _{1s^{2}} \end{array} \) |
I1 = 520.2 |
\( \begin{array}{lcl} Be\left ( g \right ) & \rightarrow & Be^{+}+e^{-} \\ _{1s^{2}2s^{2}} & = & _{1s^{2}2s^{1}} \end{array} \) |
I1 = 899.5 |
|
\( \begin{array}{lcl} Li^{2+}\left ( g \right ) & \rightarrow & Li^{3+}+e^{-} \\ _{1s^{1}} & = & _{1s^{0}} \end{array} \) |
I2 = 7298.2 |
\( \begin{array}{lcl} Be^{+}\left ( g \right ) & \rightarrow & Be^{2+}+e^{-} \\ _{1s^{2}2s^{1}} & = & _{1s^{2}} \end{array} \) |
I2 = 1757.1 |
|
\( \begin{array}{lcl} Li^{2+}\left ( g \right ) & \rightarrow & Li^{3+}+e^{-} \\ _{1s^{1}} & = & _{1s^{0}} \end{array} \) |
I3 = 11,815.0 |
\( \begin{array}{lcl} Be^{2+}\left ( g \right ) & \rightarrow & Be^{3+}+e^{-} \\ _{1s^{2}} & = & _{1s^{1}} \end{array} \) |
I3 = 14,848.8 |
|
\( \begin{array}{lcl} Be^{3+}\left ( g \right ) & \rightarrow & Be^{4+}+e^{-} \\ _{1s^{1}} & = & _{1s^{0}} \end{array} \) |
I4 = 21,006.6 |
Source: Data from CRC Handbook of Chemistry and Physics (2004).
The most important consequence of the values listed in Table 3.2.1 is that the chemistry of \(Li\) is dominated by the \(Li^+\) ion, while the chemistry of \(Be\) is dominated by the +2 oxidation state. The energy required to remove the second electron from \(Li\)
\[Li^+_{(g)} \rightarrow Li^{2+}_{(g)} + e^−\]
is more than 10 times greater than the energy needed to remove the first electron. Similarly, the energy required to remove the third electron from \(Be\)
\[Be^{2+}_{(g)} \rightarrow Be^{3+}_{(g)} + e^−\]
is about 15 times greater than the energy needed to remove the first electron and around 8 times greater than the energy required to remove the second electron. Both \(Li^+\) and \(Be^{2+}\) have \(1s^2\) closed-shell configurations, and much more energy is required to remove an electron from the 1s2 core than from the 2s valence orbital of the same element. The chemical consequences are enormous: lithium (and all the alkali metals) forms compounds with the 1+ ion but not the 2+ or 3+ ions. Similarly, beryllium (and all the alkaline earth metals) forms compounds with the 2+ ion but not the 3+ or 4+ ions. The energy required to remove electrons from a filled core is prohibitively large and simply cannot be achieved in normal chemical reactions.
Note the Pattern
The energy required to remove electrons from a filled core is prohibitively large under normal reaction conditions.
Ionization Energies of s- and p-Block Elements
Ionization energies of the elements in the third row of the periodic table exhibit the same pattern as those of Li and Be (Table 3.2.2 ): successive ionization energies increase steadily as electrons are removed from the valence orbitals (3s or 3p, in this case), followed by an especially large increase in ionization energy when electrons are removed from filled core levels as indicated by the bold diagonal line in Table 3.2.2 . Thus in the third row of the periodic table, the largest increase in ionization energy corresponds to removing the fourth electron from Al, the fifth electron from Si, and so forth—that is, removing an electron from an ion that has the valence electron configuration of the preceding noble gas. This pattern explains why the chemistry of the elements normally involves only valence electrons. Too much energy is required to either remove or share the inner electrons.
Table 3.2.2 Successive Ionization Energies (in kJ/mol) for the Elements in the Third Row of the Periodic Table
| Element | I 1 | I 2 | I 3 | I 4 | I 5 | I 6 | I 7 |
|---|---|---|---|---|---|---|---|
| Na | 495.8 | 4562.4* | — | — | — | — | — |
| Mg | 737.7 | 1450.7 | 7732.7 | — | — | — | — |
| Al | 577.5 | 1816.7 | 2744.8 | 11,577.5 | — | — | — |
| Si | 786.5 | 1577.1 | 3231.6 | 4355.5 | 16,090.6 | — | — |
| P | 1011.8 | 1907.5 | 2914.1 | 4963.6 | 6274.0 | 21,267.4 | — |
| S | 999.6 | 2251.8 | 3357 | 4556.2 | 7004.3 | 8495.8 | 27,107.4 |
| Cl | 1251.2 | 2297.7 | 3822 | 5158.6 | 6540 | 9362 | 11,018.2 |
| Ar | 1520.6 | 2665.9 | 3931 | 5771 | 7238 | 8781.0 | 11,995.3 |
| *Inner-shell electron | |||||||
Source: Data from CRC Handbook of Chemistry and Physics (2004).
Example 3.2.1
From their locations in the periodic table, predict which of these elements has the highest fourth ionization energy: B, C, or N.
Given: three elements
Asked for: element with highest fourth ionization energy
Strategy:
A List the electron configuration of each element.
B Determine whether electrons are being removed from a filled or partially filled valence shell. Predict which element has the highest fourth ionization energy, recognizing that the highest energy corresponds to the removal of electrons from a filled electron core.
Solution:
A These elements all lie in the second row of the periodic table and have the following electron configurations:
B: [He]2s22p1 C: [He]2s22p2 N: [He]2s22p3
B The fourth ionization energy of an element (I4) is defined as the energy required to remove the fourth electron:
E3+(g) → E4+(g) + e−
Because carbon and nitrogen have four and five valence electrons, respectively, their fourth ionization energies correspond to removing an electron from a partially filled valence shell. The fourth ionization energy for boron, however, corresponds to removing an electron from the filled 1s2 subshell. This should require much more energy. The actual values are as follows: B, 25,026 kJ/mol; C, 6223 kJ/mol; and N, 7475 kJ/mol.
Exercise
From their locations in the periodic table, predict which of these elements has the lowest second ionization energy: Sr, Rb, or Ar.
Answer: Sr
The first column of data in Table 3.2.2 shows that first ionization energies tend to increase across the third row of the periodic table. This is because the valence electrons do not screen each other very well, allowing the effective nuclear charge to increase steadily across the row. The valence electrons are therefore attracted more strongly to the nucleus, so atomic sizes decrease and ionization energies increase. These effects represent two sides of the same coin: stronger electrostatic interactions between the electrons and the nucleus further increase the energy required to remove the electrons.
However, the first ionization energy decreases at Al ([Ne]3s23p1) and at S ([Ne]3s23p4). The electrons in aluminum’s filled 3s2 subshell are better at screening the 3p1 electron than they are at screening each other from the nuclear charge, so the s electrons penetrate closer to the nucleus than the p electron does. The decrease at S occurs because the two electrons in the same p orbital repel each other. This makes the S atom slightly less stable than would otherwise be expected, as is true of all the group 16 elements.
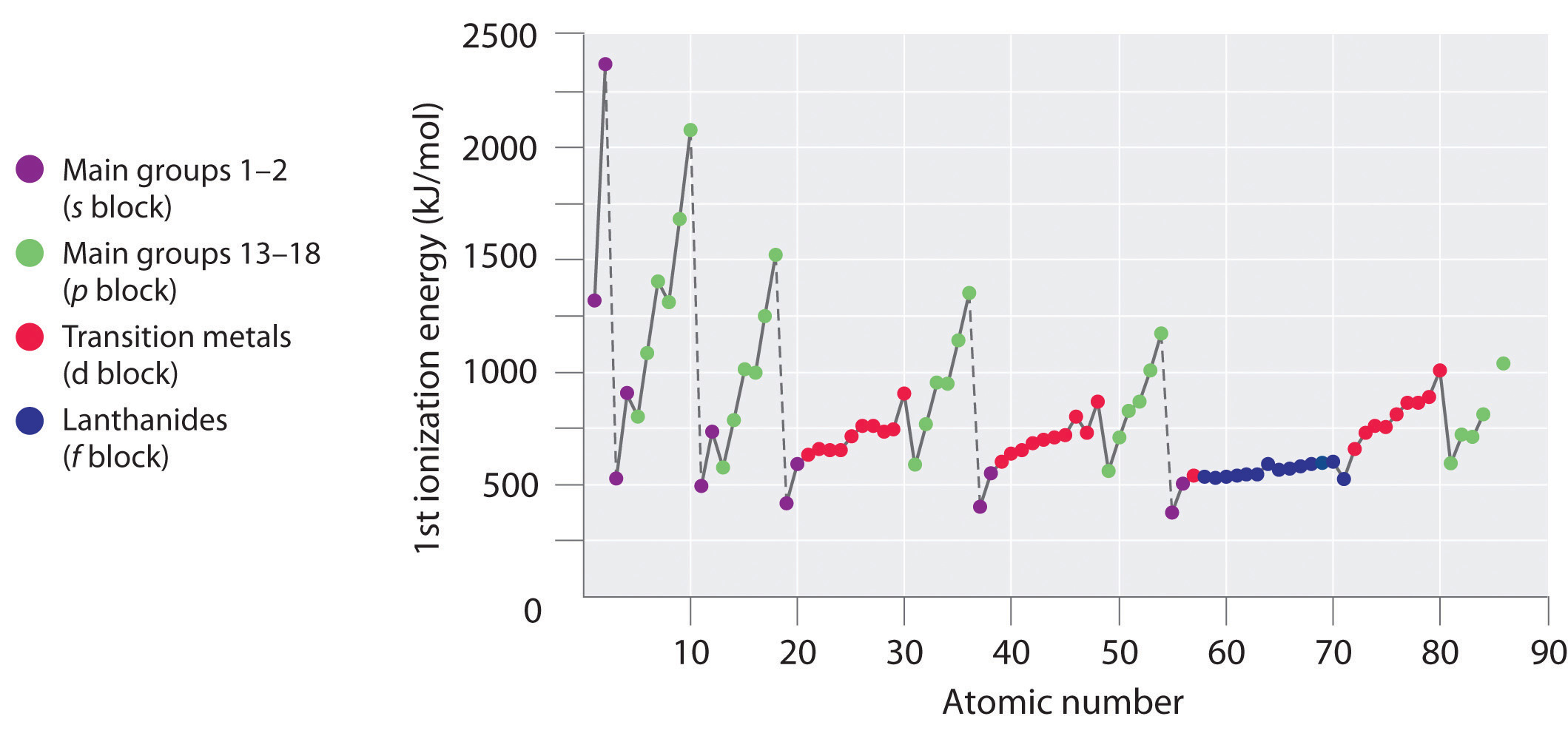
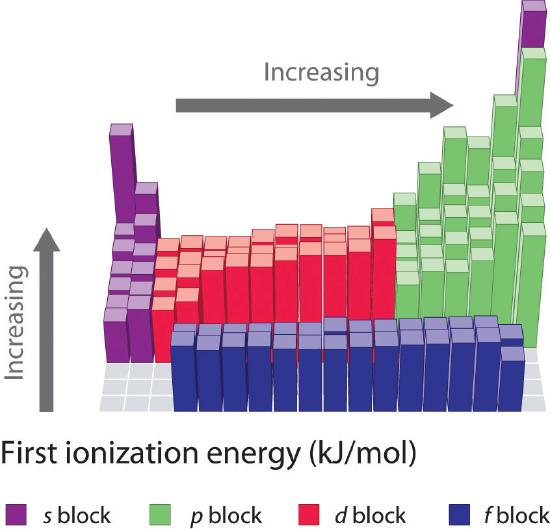
The first ionization energies of the elements in the first six rows of the periodic table are plotted in Figure 3.2.1 . They are presented numerically and graphically in Figure 3.2.2 . These figures illustrate three important trends:
- The changes seen in the second (Li to Ne), fourth (K to Kr), fifth (Rb to Xe), and sixth (Cs to Rn) rows of the s and p blocks follow a pattern similar to the pattern described for the third row of the periodic table. The transition metals are included in the fourth, fifth, and sixth rows, however, and the lanthanides are included in the sixth row. The first ionization energies of the transition metals are somewhat similar to one another, as are those of the lanthanides. Ionization energies increase from left to right across each row, with discrepancies occurring at ns2np1 (group 13), ns2np4 (group 16), and ns2(n − 1)d10 (group 12) electron configurations.
- First ionization energies generally decrease down a column. Although the principal quantum number n increases down a column, filled inner shells are effective at screening the valence electrons, so there is a relatively small increase in the effective nuclear charge. Consequently, the atoms become larger as they acquire electrons. Valence electrons that are farther from the nucleus are less tightly bound, making them easier to remove, which causes ionization energies to decrease. A larger radius corresponds to a lower ionization energy.
- Because of the first two trends, the elements that form positive ions most easily (have the lowest ionization energies) lie in the lower left corner of the periodic table, whereas those that are hardest to ionize lie in the upper right corner of the periodic table. Consequently, ionization energies generally increase diagonally from lower left (Cs) to upper right (He).
Note the Pattern
Generally, I1 increases diagonally from the lower left of the periodic table to the upper right.
Figure 3.2.1 A Plot of Periodic Variation of First Ionization Energy with Atomic Number for the First Six Rows of the Periodic Table There is a decrease in ionization energy within a group (most easily seen here for groups 1 and 18). Can you explain the breaks in Figure 3.10 based on what you know about atomic structure and filled and half filled orbitals? Note the break after two electrons fill the ns orbitals and three the np orbitals. What does this say about ionizing half filled shells.
Figure 3.2.2 A Bar Chart of the Periodic Variation of First Ionization Energy with Atomic Number for the First Six Rows of the Periodic Table
Figure 3.2.3 First Ionization Energies of the s-, p-, d-, and f-Block Elements The darkness of the shading inside the cells of the table indicates the relative magnitudes of the ionization energies. Elements in gray have undetermined first ionization energies. Source: Data from CRC Handbook of Chemistry and Physics (2004). The CRC Handbook is a basic reference for Chemistry, Physics and Engineering. Every science and engineering major should own a copy. There are special student editions.
Gallium (Ga), which is the first element following the first row of transition metals, has the electron configuration: [Ar]4s23d104p1. Its first ionization energy is significantly lower than that of the immediately preceding element, zinc, because the filled 3d10 subshell of gallium lies inside the 4p subshell, screening the single 4p electron from the nucleus. Experiments have revealed something of even greater interest: the second and third electrons that are removed when gallium is ionized come from the 4s2 orbital, not the 3d10 subshell. The chemistry of gallium is dominated by the resulting Ga3+ ion, with its [Ar]3d10 electron configuration. This and similar electron configurations are particularly stable and are often encountered in the heavier p-block elements. They are sometimes referred to as pseudo noble gas configurations The (n-1)d10and similar electron configurations that are particularly stable and are often encountered in the heavier p-block elements.. In fact, for elements that exhibit these configurations, no chemical compounds are known in which electrons are removed from the (n − 1)d10 filled subshell.
Ionization Energies of Transition Metals and Lanthanides
As we noted, the first ionization energies of the transition metals and the lanthanides change very little across each row. Differences in their second and third ionization energies are also rather small, in sharp contrast to the pattern seen with the s- and p-block elements. The reason for these similarities is that the transition metals and the lanthanides form cations by losing the ns electrons before the (n − 1)d or (n − 2)f electrons, respectively. This means that transition metal cations have (n − 1)dn valence electron configurations, and lanthanide cations have (n − 2)fn valence electron configurations. Because the (n − 1)d and (n − 2)f shells are closer to the nucleus than the ns shell, the (n − 1)d and (n − 2)f electrons screen the ns electrons quite effectively, reducing the effective nuclear charge felt by the ns electrons. As Z increases, the increasing positive charge is largely canceled by the electrons added to the (n − 1)d or (n − 2)f orbitals.
That the ns electrons are removed before the (n − 1)d or (n − 2)f electrons may surprise you because the orbitals were filled in the reverse order. (For more information on shell filling order, see Section 2.3 .) In fact, the ns, the (n − 1)d, and the (n − 2)f orbitals are so close to one another in energy, and interpenetrate one another so extensively, that very small changes in the effective nuclear charge can change the order of their energy levels. As the d orbitals are filled, the effective nuclear charge causes the 3d orbitals to be slightly lower in energy than the 4s orbitals. The [Ar]3d2 electron configuration of Ti2+ tells us that the 4s electrons of titanium are lost before the 3d electrons; this is confirmed by experiment. A similar pattern is seen with the lanthanides, producing cations with an (n − 2)fn valence electron configuration.
Because their first, second, and third ionization energies change so little across a row, these elements have important horizontal similarities in chemical properties in addition to the expected vertical similarities. For example, all the first-row transition metals except scandium form stable compounds as M2+ ions, whereas the lanthanides primarily form compounds in which they exist as M3+ ions.
Example 3.2.2
Use their locations in the periodic table to predict which element has the lowest first ionization energy: Ca, K, Mg, Na, Rb, or Sr.
Given: six elements
Asked for: element with lowest first ionization energy
Strategy:
Locate the elements in the periodic table. Based on trends in ionization energies across a row and down a column, identify the element with the lowest first ionization energy.
Solution:
These six elements form a rectangle in the two far-left columns of the periodic table. Because we know that ionization energies increase from left to right in a row and from bottom to top of a column, we can predict that the element at the bottom left of the rectangle will have the lowest first ionization energy: Rb.
Exercise
Use their locations in the periodic table to predict which element has the highest first ionization energy: As, Bi, Ge, Pb, Sb, or Sn.
Answer: As
Electron Affinities
The electron affinity (EA)The energy change that occurs when an electron is added to a gaseous atom: E(g) + e- → E-(g) of an element E is defined as the energy change that occurs when an electron is added to a gaseous atom:
\( E\left ( g \right )+e^{-}\rightarrow E\left ( g \right )^{-} \; \; \; \; energy\; change=Ea \tag{3.2.5} \)
Unlike ionization energies, which are always positive for a neutral atom because energy is required to remove an electron, electron affinities can be negative (energy is released when an electron is added), positive (energy must be added to the system to produce an anion), or zero (the process is energetically neutral). This sign convention is consistent with our discussion of energy changes later in the course, where a negative value corresponded to the energy change for an exothermic process, which is one in which heat is released. Such a process represents a loss of energy from the chemicals in a reaction.
Chlorine has the most negative electron affinity of any element, which means that more energy is released when an electron is added to a gaseous chlorine atom than to an atom of any other element:
\( Cl\left ( g \right )+e^{-}\rightarrow Cl\left ( g \right )^{-} \; \; \; \; Ea=-348.6\; kJ/mol\; \; \; \; \tag{3.2.6} \)
In contrast, beryllium does not form a stable anion, so its effective electron affinity is
\( Be\left ( g \right )+e^{-}\rightarrow Be\left ( g \right )^{-} \; \; \; \; Ea\geq 0\; kJ/mol\; \; \; \; \tag{3.2.7} \)
Nitrogen is unique in that it has an electron affinity of approximately zero. Adding an electron neither releases nor requires a significant amount of energy. We might remember that nitrogen has a half filled p orbital which adds to its stability:
\( N\left ( g \right )+e^{-}\rightarrow N\left ( g \right )^{-} \; \; \; \; Ea\approx\; kJ/mol\; \; \; \; \tag{3.2.8} \)
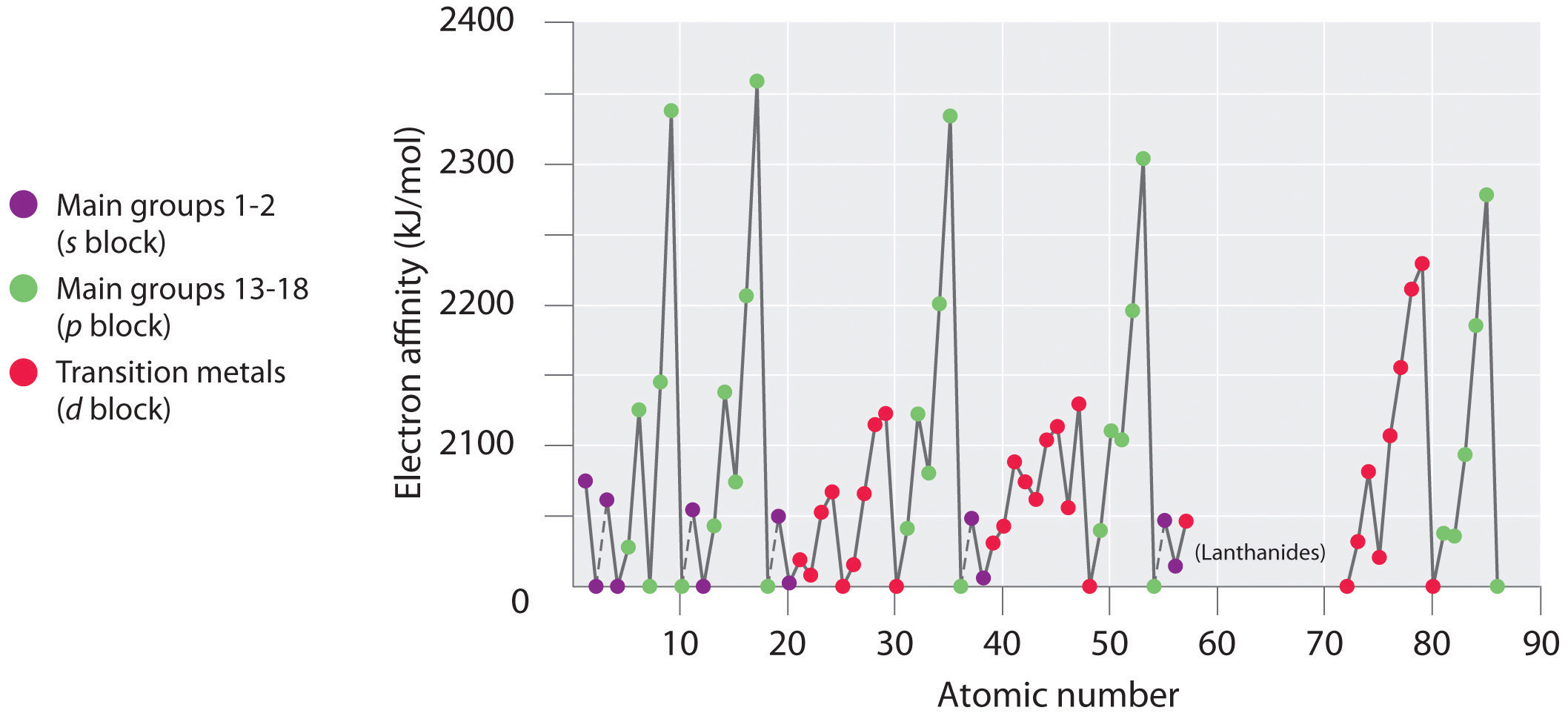
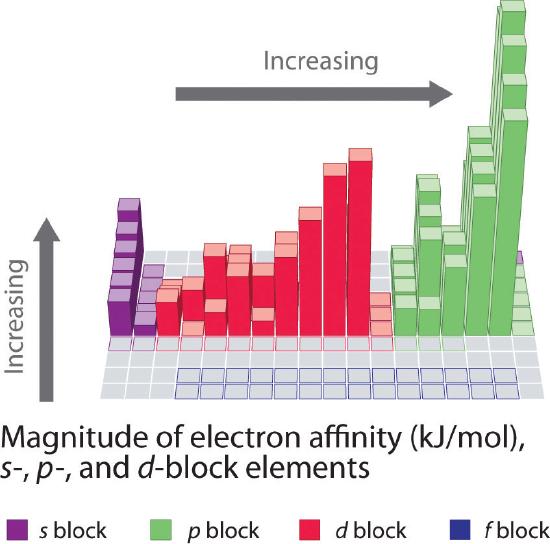
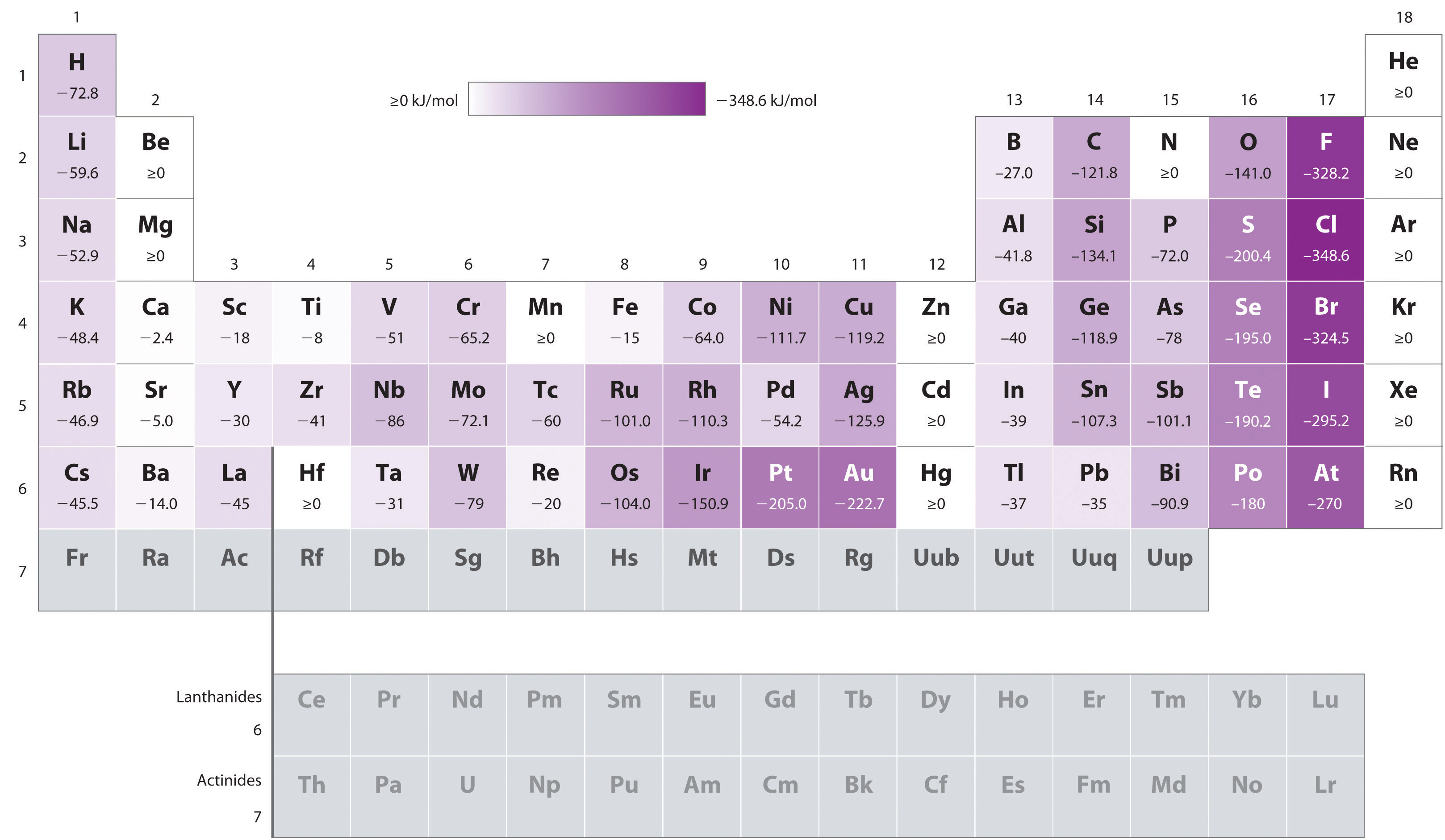
Electron affinities for the first six rows of the periodic table are plotted in Figure 3.2.4 and presented numerically and graphically in Figure 3.2.6 . Both figures show that the halogens, with their ns2np5 valence electron configuration, have the most negative electron affinities. In general, electron affinities become more negative as we go across a row of the periodic table. This pattern corresponds to the increased effective nuclear charge felt by the valence electrons across a row, which leads to increased electrostatic attraction between the added electron and the nucleus (a more negative electron affinity). The trend, however, is not as uniform as the one observed for ionization energies. Some of the alkaline earths (group 2), the elements of group 12, and all the noble gases (group 18) have effective electron affinities that are greater than or equal to zero, while the electron affinities for the elements of group 15 are usually less negative than those for the group 14 elements. These exceptions can be explained by the groups’ electron configurations. Both the alkaline earth metals and the noble gases have valence electron shells with filled subshells (ns2 and ns2np6, respectively). In each case, the added electron must enter a higher-energy orbital, requiring an input of energy. All the group 15 elements have an ns2np3 valence electron configuration, in which each of the three p orbitals has a single electron, in accordance with Hund’s rule; hence the added electron must enter an already occupied p orbital. The resulting electron–electron repulsions destabilize the anion, causing the electron affinities of these elements to be less negative than we would otherwise expect. In the case of nitrogen, the 2p orbital is quite small, and the electron–electron repulsions are so strong that nitrogen has approximately zero affinity for an extra electron. In the heavier elements, however, the effect is relatively small because they have larger valence p orbitals.
Note the Pattern
Generally, electron affinities become more negative across a row of the periodic table.
Figure 3.2.4 A Plot of Periodic Variation of Electron Affinity with Atomic Number for the First Six Rows of the Periodic TableCan you explain the breaks in Figure 3.2.4 based on what you know about atomic structure and filled and half filled orbitals? This is more difficult than the equivalent for ionization energy.
Figure 3.2.5 Bar Chart of the Periodic Variation of Electron Affinity with Atomic Number for the First Six Rows of the Periodic Table
Figure 3.2.6 Electron Affinities (in kJ/mol) of the s-, p-, and d-Block Elements There are many more exceptions to the trends across rows and down columns than with first ionization energies. Elements that do not form stable ions, such as the noble gases, are assigned an effective electron affinity that is greater than or equal to zero. Elements for which no data are available are shown in gray. Source: Data from Journal of Physical and Chemical Reference Data 28, no. 6 (1999).
In general, electron affinities of the main-group elements become less negative as we proceed down a column. This is because as n increases, the extra electrons enter orbitals that are increasingly far from the nucleus. Atoms with the largest radii, which have the lowest ionization energies (affinity for their own valence electrons), also have the lowest affinity for an added electron. There are, however, two major exceptions to this trend:
- The electron affinities of elements B through F in the second row of the periodic table are less negative than those of the elements immediately below them in the third row. Apparently, the increased electron–electron repulsions experienced by electrons confined to the relatively small 2p orbitals overcome the increased electron–nucleus attraction at short nuclear distances. Fluorine, therefore, has a lower affinity for an added electron than does chlorine. Consequently, the elements of the third row (n = 3) have the most negative electron affinities. Farther down a column, the attraction for an added electron decreases because the electron is entering an orbital more distant from the nucleus. Electron–electron repulsions also decrease because the valence electrons occupy a greater volume of space. These effects tend to cancel one another, so the changes in electron affinity within a family are much smaller than the changes in ionization energy.
- The electron affinities of the alkaline earth metals become more negative from Be to Ba. As you learned in Chapter 2, the energy separation between the filled ns2 and the empty np subshells decreases with increasing n, so that formation of an anion from the heavier elements becomes energetically more favorable.
Note the Pattern
In general, electron affinities become more negative across a row and less negative down a column.
The equations for second and higher electron affinities are analogous to those for second and higher ionization energies:
\( E\left ( g \right )+ e^{-}\rightarrow E\left ( g \right )^{-}\; \; energy\; change\; =Ea_{1} \; \tag{3.2.9} \)
\( E\left ( g \right )^{-}+ e^{-}\rightarrow E\left ( g \right )^{2-}\; \; energy\; change\; =Ea_{2} \; \tag{3.2.10} \)
As we have seen, the first electron affinity can be greater than or equal to zero or negative, depending on the electron configuration of the atom. In contrast, the second electron affinity is always positive because the increased electron–electron repulsions in a dianion are far greater than the attraction of the nucleus for the extra electrons. For example, the first electron affinity of oxygen is −141 kJ/mol, but the second electron affinity is +744 kJ/mol:
\( O\left ( g \right )+ e^{-}\rightarrow O\left ( g \right )^{-}\; \; Ea_{}=-141\; kJ/mol \; \tag{3.2.11} \)
Thus the formation of a gaseous oxide (O2−) ion is energetically quite unfavorable:
\( O\left ( g \right )+ 2e^{-}\rightarrow O\left ( g \right )^{2-}\; \; Ea_{1}+Ea_{2}=+603\; kJ/mol \; \tag{3.2.12} \)
Similarly, the formation of all common dianions (such as S2−) or trianions (such as P3−) is energetically unfavorable in the gas phase.
Note the Pattern
While first electron affinities can be negative, positive, or zero, second electron affinities are always positive.
If energy is required to form both positively charged ions and monatomic polyanions, why do ionic compounds such as MgO, Na2S, and Na3P form at all? The key factor in the formation of stable ionic compounds is the favorable electrostatic interactions between the cations and the anions in the crystalline salt. We will describe the energetics of ionic compounds in more detail in Chapter 4 "Chemical Bonding".
Example 3.2.3
Based on their positions in the periodic table, which of Sb, Se, or Te would you predict to have the most negative electron affinity?
Given: three elements
Asked for: element with most negative electron affinity
Strategy:
A Locate the elements in the periodic table. Use the trends in electron affinities going down a column for elements in the same group. Similarly, use the trends in electron affinities from left to right for elements in the same row.
B Place the elements in order, listing the element with the most negative electron affinity first.
Solution:
A We know that electron affinities become less negative going down a column (except for the anomalously low electron affinities of the elements of the second row), so we can predict that the electron affinity of Se is more negative than that of Te. We also know that electron affinities become more negative from left to right across a row, and that the group 15 elements tend to have values that are less negative than expected. Because Sb is located to the left of Te and belongs to group 15, we predict that the electron affinity of Te is more negative than that of Sb. The overall order is Se < Te < Sb, so Se has the most negative electron affinity among the three elements.
Exercise
Based on their positions in the periodic table, which of Rb, Sr, or Xe would you predict to most likely form a gaseous anion?
Answer: Rb
Electronegativity
The elements with the highest ionization energies are generally those with the most negative electron affinities, which are located toward the upper right corner of the periodic table (compare Figure 3.2.1 ). Conversely, the elements with the lowest ionization energies are generally those with the least negative electron affinities and are located in the lower left corner of the periodic table.
Because the tendency of an element to gain or lose electrons is so important in determining its chemistry, various methods have been developed to quantitatively describe this tendency. The most important method uses a measurement called electronegativityThe relative ability of an atom to attract electrons to itself in a chemical compound. (represented by the Greek letter chi, χ, pronounced “ky” as in “sky”), defined as the relative ability of an atom to attract electrons to itself in a chemical compound. Elements with high electronegativities tend to acquire electrons in chemical reactions and are found in the upper right corner of the periodic table. Elements with low electronegativities tend to lose electrons in chemical reactions and are found in the lower left corner of the periodic table.
Unlike ionization energy or electron affinity, the electronegativity of an atom is not a simple, fixed property that can be directly measured in a single experiment. In fact, an atom’s electronegativity should depend to some extent on its chemical environment because the properties of an atom are influenced by its neighbors in a chemical compound. Nevertheless, when different methods for measuring the electronegativity of an atom are compared, they all tend to assign similar relative values to a given element. For example, all scales predict that fluorine has the highest electronegativity and cesium the lowest of the stable elements, which suggests that all the methods are measuring the same fundamental property.
The Pauling Electronegativity Scale
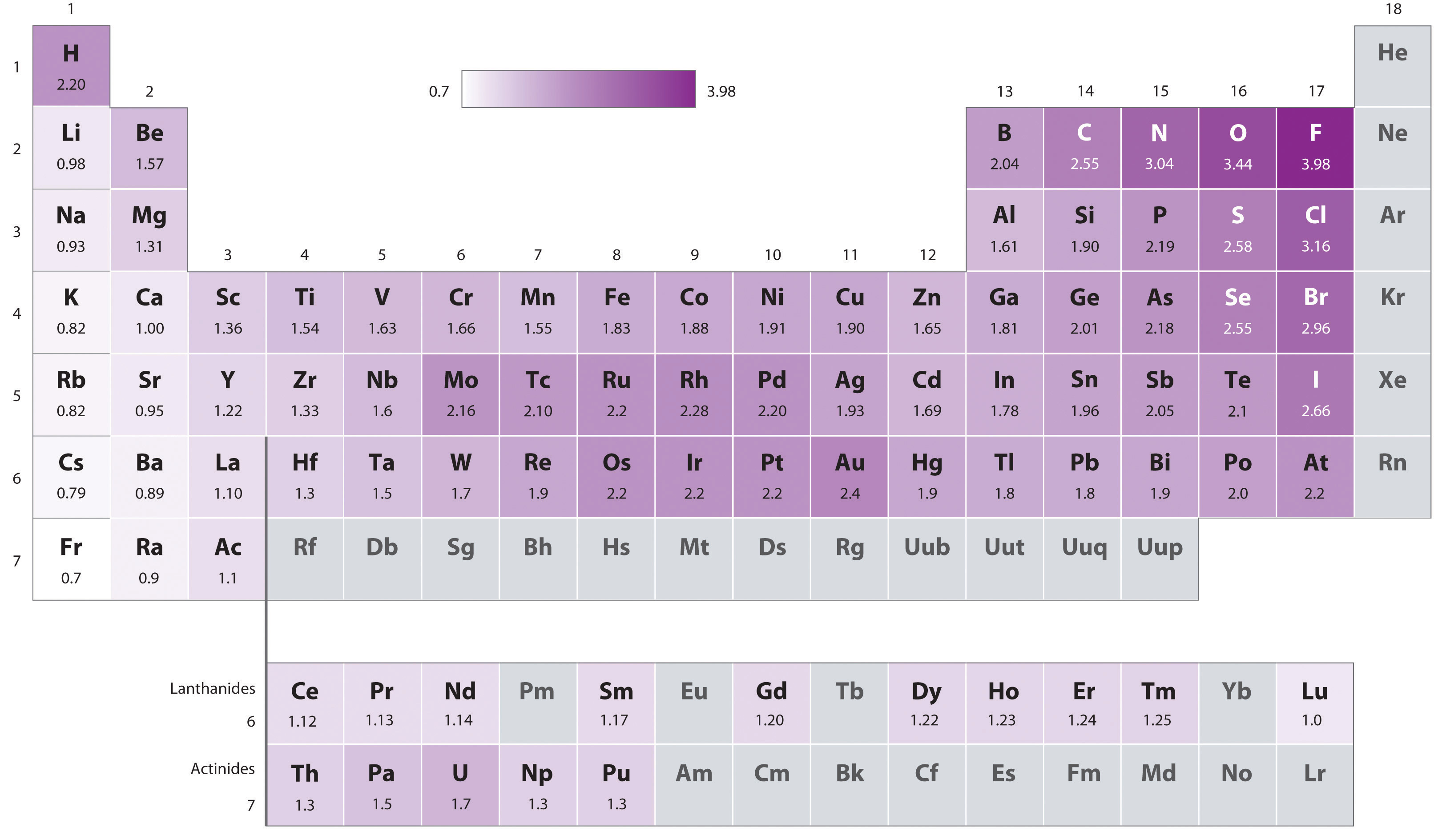
The original electronegativity scale, developed in the 1930s by Linus Pauling (1901– 1994) was based on measurements of the strengths of covalent bonds between different elements. Pauling arbitrarily set the electronegativity of fluorine at 4.0 (although today it has been refined to 3.98), thereby creating a scale in which all elements have values between 0 and 4.0.
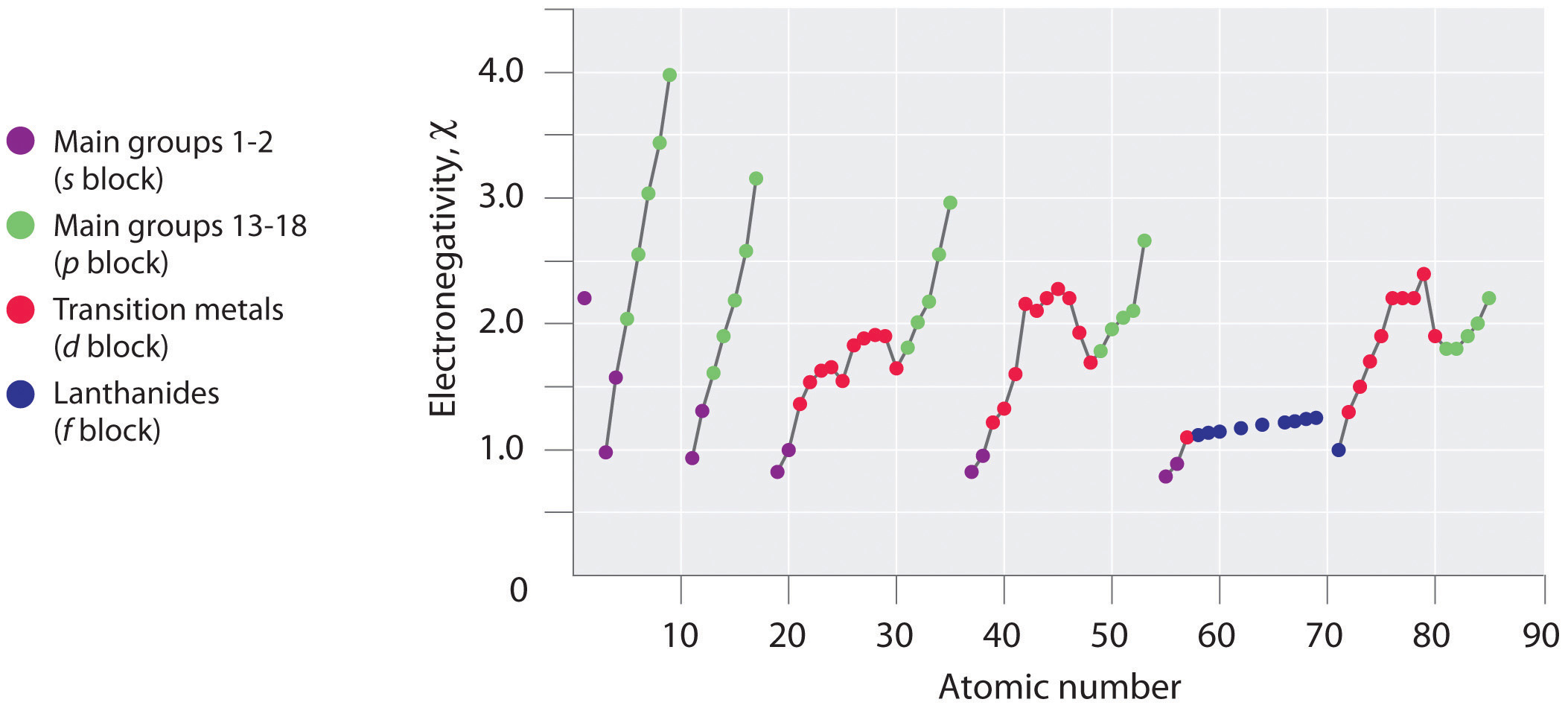
Periodic variations in Pauling’s electronegativity values are illustrated in Figure 3.2.7 and Figure 3.2.9 . If we ignore the inert gases and elements for which no stable isotopes are known, we see that fluorine (χ = 3.98) is the most electronegative element and cesium is the least electronegative nonradioactive element (χ = 0.79). Because electronegativities generally increase diagonally from the lower left to the upper right of the periodic table, elements lying on diagonal lines running from upper left to lower right tend to have comparable values (e.g., O and Cl and N, S, and Br).
Figure 3.2.7 A Plot of Periodic Variation of Electronegativity with Atomic Number for the First Six Rows of the Periodic Table
Can you explain the breaks in Figure 3.2.7 based on what you know about atomic structure and filled and half filled d orbitals? Note how the electronegativity dependence on atomic number is smoother than the ionization and electron affinity.
Linus Pauling (1901–1994)
Pauling won two Nobel Prizes, one for chemistry in 1954 and one for peace in 1962. When he was nine, Pauling’s father died, and his mother tried to convince him to quit school to support the family. He did not quit school but was denied a high school degree because of his refusal to take a civics class.
Figure 3.2.9 Pauling Electronegativity Values of the s-, p-, d-, and f-Block ElementsValues for most of the actinides are approximate. Elements for which no data are available are shown in gray. Source: Data from L. Pauling, The Nature of the Chemical Bond, 3rd ed. (1960).
Pauling’s method is limited by the fact that many elements do not form stable covalent compounds with other elements; hence their electronegativities cannot be measured by his method. Other definitions have since been developed that address this problem.
The Mulliken Definition
An alternative method for measuring electronegativity was developed by Robert Mulliken (1896–1986; Nobel Prize in Chemistry 1966). Mulliken noticed that elements with large first ionization energies tend to have very negative electron affinities and gain electrons in chemical reactions. Conversely, elements with small first ionization energies tend to have slightly negative (or even positive) electron affinities and lose electrons in chemical reactions. Mulliken recognized that an atom’s tendency to gain or lose electrons could therefore be described quantitatively by the average of the values of its first ionization energy and the absolute value of its electron affinity. Using our definition of electron affinity, we can write Mulliken’s original expression for electronegativity as follows:Mulliken’s definition used the magnitude of the ionization energy and the electron affinity. By definition, the magnitude of a quantity is a positive number. Our definition of electron affinity produces negative values for the electron affinity for most elements, so vertical lines indicating absolute value are needed in Equation 3.2.13 to make sure that we are adding two positive numbers in the numerator.
\( x = \frac{I+\left | EA \right |}{2}\; \tag{3.2.13} \)
Bearing in mind that the magnitude of ionization energies are generally large compared to the those of electron affinities, elements with a large first ionization energy and a very negative electron affinity have a large positive value in the numerator of Equation 3.2.13 so their electronegativity is high. Elements with a small first ionization energy and a small electron affinity have a small positive value for the numerator in Equation 3.2.13, so they have a low electronegativity.Inserting the appropriate data for ionization energy and electron affinity into Equation 3.2.13 gives a Mulliken electronegativity value for fluorine of 1004.6 kJ/mol. To compare Mulliken’s electronegativity values with those obtained by Pauling, Mulliken’s values are divided by 252.4 kJ/mol, which gives Pauling’s value (3.98).
As noted previously, all electronegativity scales give essentially the same results for one element relative to another. Even though the Mulliken scale is based on the properties of individual atoms and the Pauling scale is based on the properties of atoms in molecules, they both apparently measure the same basic property of an element. In the following discussion, we will focus on the relationship between electronegativity and the tendency of atoms to form positive or negative ions. We will therefore be implicitly using the Mulliken definition of electronegativity. Because of the parallels between the Mulliken and Pauling definitions, however, the conclusions are likely to apply to atoms in molecules as well.
Electronegativity Differences between Metals and Nonmetals
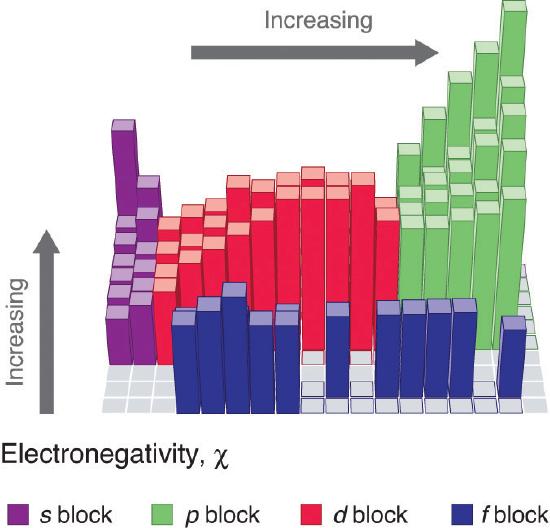
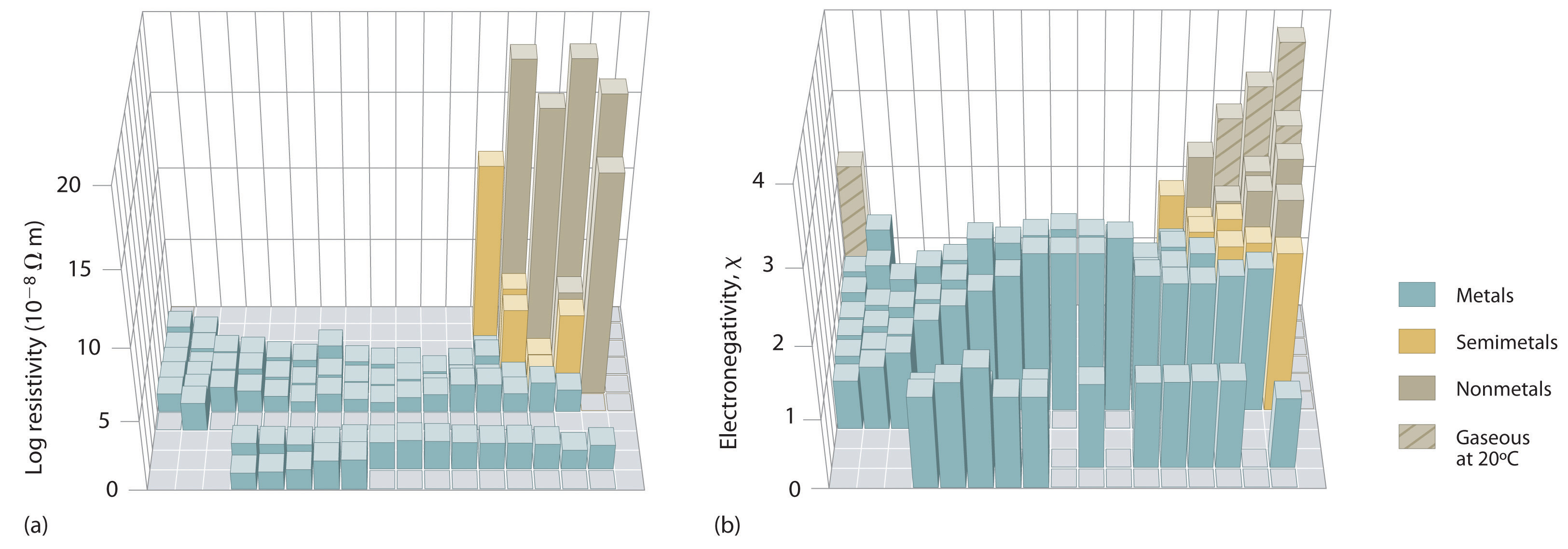
An element’s electronegativity provides us with a single value that we can use to characterize the chemistry of an element. Elements with a high electronegativity (χ ≥ 2.2 in Figure 3.2.9 ) have very negative electron affinities and large ionization potentials, so they are generally nonmetals and electrical insulators that tend to gain electrons in chemical reactions (i.e., they are oxidants). In contrast, elements with a low electronegativity (χ ≤ 1.8) have electron affinities that have either positive or small negative values and small ionization potentials, so they are generally metals and good electrical conductors that tend to lose their valence electrons in chemical reactions (i.e., they are reductants). In between the metals and nonmetals, along the diagonal line running from B to At is a group of elements with intermediate electronegativities (χ ~ 2.0). These are the semimetals, elements that have some of the chemical properties of both nonmetals and metals. The distinction between metals and nonmetals is one of the most fundamental we can make in categorizing the elements and predicting their chemical behavior. Figure 3.2.10 shows the strong correlation between electronegativity values, metallic versus nonmetallic character, and location in the periodic table.
Figure 3.2.10 Three-Dimensional Plots Demonstrating the Relationship between Electronegativity and the Metallic/Nonmetallic Character of the Elements (a) A plot of electrical resistivity (measured resistivity to electron flow) at or near room temperature shows that substances with high resistivity (little to no measured electron flow) are electrical insulators, whereas substances with low resistivity (high measured electron flow) are metals. (b) A plot of Pauling electronegativities for a like set of elements shows that high electronegativity values (≥ about 2.2) correlate with high electrical resistivities (insulators). Low electronegativity values (≤ about 2.2) correlate with low resistivities (metals). Because electrical resistivity is typically measured only for solids and liquids, the gaseous elements do not appear in part (a).
Example 3.2.4
On the basis of their positions in the periodic table, arrange Cl, Se, Si, and Sr in order of increasing electronegativity and classify each as a metal, a nonmetal, or a semimetal.
Given: four elements
Asked for: order by increasing electronegativity and classification
Strategy:
A Locate the elements in the periodic table. From their diagonal positions from lower left to upper right, predict their relative electronegativities.
B Arrange the elements in order of increasing electronegativity.
C Classify each element as a metal, a nonmetal, or a semimetal according to its location about the diagonal belt of semimetals running from B to At.
Solution:
A Electronegativity increases from lower left to upper right in the periodic table (Figure 3.2.8 ). Because Sr lies far to the left of the other elements given, we can predict that it will have the lowest electronegativity. Because Cl lies above and to the right of Se, we can predict that χCl > χSe. Because Si is located farther from the upper right corner than Se or Cl, its electronegativity should be lower than those of Se and Cl but greater than that of Sr. B The overall order is therefore χSr < χSi < χSe < χCl.
C To classify the elements, we note that Sr lies well to the left of the diagonal belt of semimetals running from B to At; while Se and Cl lie to the right and Si lies in the middle. We can predict that Sr is a metal, Si is a semimetal, and Se and Cl are nonmetals.
Exercise
On the basis of their positions in the periodic table, arrange Ge, N, O, Rb, and Zr in order of increasing electronegativity and classify each as a metal, a nonmetal, or a semimetal.
Answer: Rb < Zr < Ge < N < O; metals (Rb, Zr); semimetal (Ge); nonmetal (N, O)
Note the Pattern
Electronegativity values increase from lower left to upper right in the periodic table.
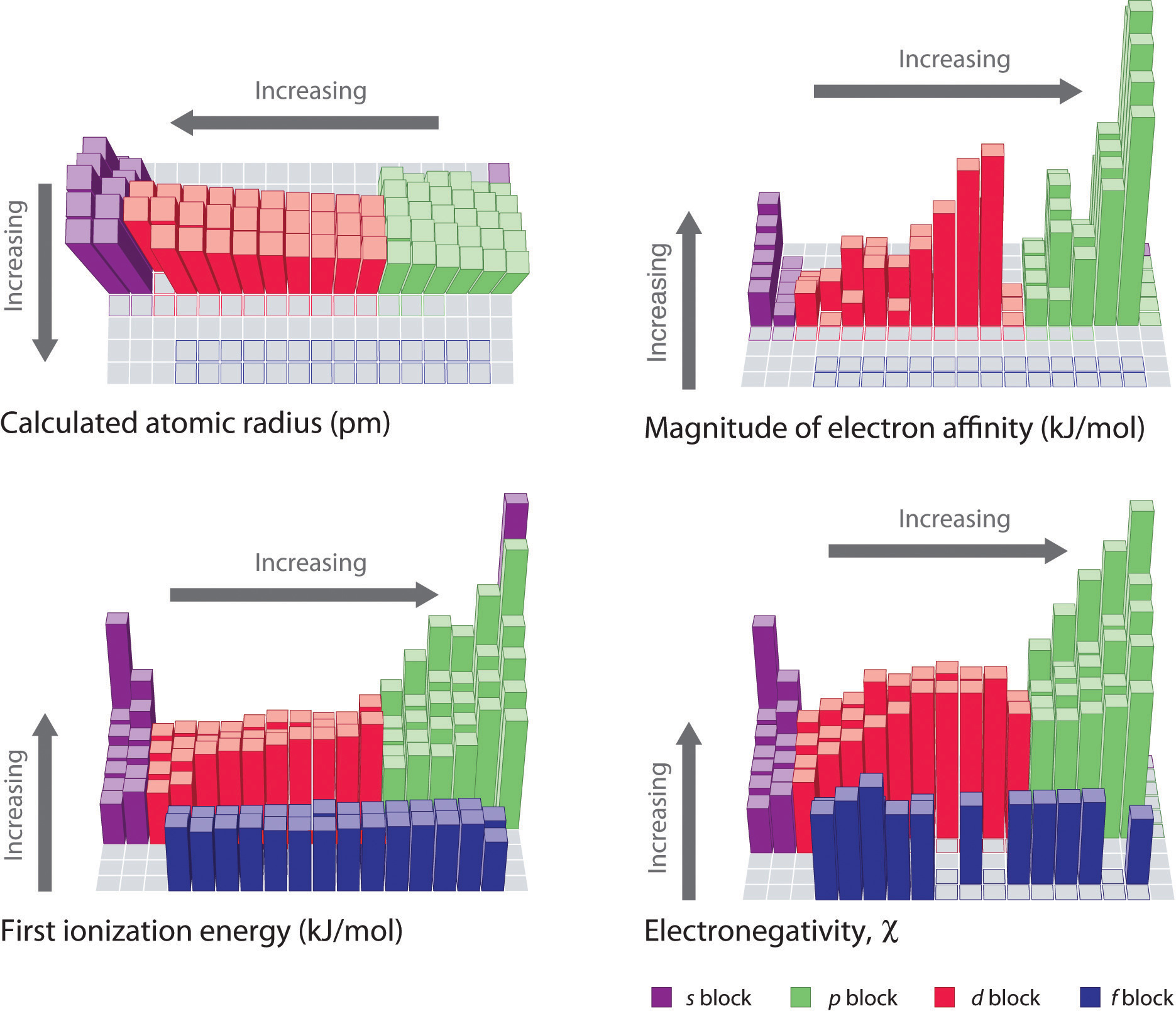
The trends in periodic properties are summarized in Figure 3.2.11. As discussed, atomic radii decrease from lower left to upper right in the periodic table; ionization energies become more positive, electron affinities become more negative, and electronegativities increase from the lower left to the upper right.
Figure 3.2.11 Summary of Major Periodic TrendsThe general trends for the first ionization energy, electron affinity, and electronegativity are opposite to the general trend for covalent atomic radius.
Summary
The tendency of an element to lose or gain electrons is one of the most important factors in determining the kind of compounds it forms. Periodic behavior is most evident for ionization energy (I), the energy required to remove an electron from a gaseous atom. The energy required to remove successive electrons from an atom increases steadily, with a substantial increase occurring with the removal of an electron from a filled inner shell. Consequently, only valence electrons can be removed in chemical reactions, leaving the filled inner shell intact. Ionization energies explain the common oxidation states observed for the elements. Ionization energies increase diagonally from the lower left of the periodic table to the upper right. Minor deviations from this trend can be explained in terms of particularly stable electronic configurations, called pseudo noble gas configurations, in either the parent atom or the resulting ion. The electron affinity (EA) of an element is the energy change that occurs when an electron is added to a gaseous atom to give an anion. In general, elements with the most negative electron affinities (the highest affinity for an added electron) are those with the smallest size and highest ionization energies and are located in the upper right corner of the periodic table. The electronegativity (χ) of an element is the relative ability of an atom to attract electrons to itself in a chemical compound and increases diagonally from the lower left of the periodic table to the upper right. The Pauling electronegativity scale is based on measurements of the strengths of covalent bonds between different atoms, whereas the Mulliken electronegativity of an element is the average of its first ionization energy and the absolute value of its electron affinity. Elements with a high electronegativity are generally nonmetals and electrical insulators and tend to behave as oxidants in chemical reactions. Conversely, elements with a low electronegativity are generally metals and good electrical conductors and tend to behave as reductants in chemical reactions.
Key Takeaway
- Generally, the first ionization energy and electronegativity values increase diagonally from the lower left of the periodic table to the upper right, and electron affinities become more negative across a row.
Conceptual Problems
-
Identify each statement as either true or false and explain your reasoning.
- Ionization energies increase with atomic radius.
- Ionization energies decrease down a group.
- Ionization energies increase with an increase in the magnitude of the electron affinity.
- Ionization energies decrease diagonally across the periodic table from He to Cs.
- Ionization energies depend on electron configuration.
- Ionization energies decrease across a row.
-
Based on electronic configurations, explain why the first ionization energies of the group 16 elements are lower than those of the group 15 elements, which is contrary to the general trend.
-
The first through third ionization energies do not vary greatly across the lanthanides. Why? How does the effective nuclear charge experienced by the ns electron change when going from left to right (with increasing atomic number) in this series?
-
Most of the first row transition metals can form at least two stable cations, for example iron(II) and iron(III). In contrast, scandium and zinc each form only a single cation, the Sc3+ and Zn2+ ions, respectively. Use the electron configuration of these elements to provide an explanation.
-
Of the elements Nd, Al, and Ar, which will readily form(s) +3 ions? Why?
-
Orbital energies can reverse when an element is ionized. Of the ions B3+, Ga3+, Pr3+, Cr3+, and As3+, in which would you expect this reversal to occur? Explain your reasoning.
-
The periodic trends in electron affinities are not as regular as periodic trends in ionization energies, even though the processes are essentially the converse of one another. Why are there so many more exceptions to the trends in electron affinities compared to ionization energies?
-
Elements lying on a lower right to upper left diagonal line cannot be arranged in order of increasing electronegativity according to where they occur in the periodic table. Why?
-
Why do ionic compounds form, if energy is required to form gaseous cations?
-
Why is Pauling’s definition of electronegativity considered to be somewhat limited?
-
Based on their positions in the periodic table, arrange Sb, O, P, Mo, K, and H in order of increasing electronegativity.
-
Based on their positions in the periodic table, arrange V, F, B, In, Na, and S in order of decreasing electronegativity.
Answers
-
-
-
-
-
Both Al and Nd will form a cation with a +3 charge. Aluminum is in Group 13, and loss of all three valence electrons will produce the Al3+ ion with a noble gas configuration. Neodymium is a lanthanide, and all of the lanthanides tend to form +3 ions because the ionization potentials do not vary greatly across the row, and a +3 charge can be achieved with many oxidants.
-
-
-
-
-
-
K < Mo ≈ Sb < P ≈ H < O
-
Numerical Problems
-
The following table gives values of the first and third ionization energies for selected elements:
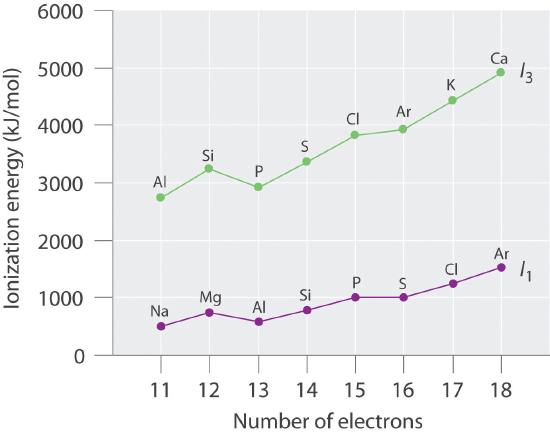
Number of Electrons Element I1 (E → E+ + e−, kJ/mol) Element I3 (E2+ → E3+ + e−, kJ/mol) 11 Na 495.9 Al 2744.8 12 Mg 737.8 Si 3231.6 13 Al 577.6 P 2914.1 14 Si 786.6 S 3357 15 P 1011.9 Cl 3822 16 S 999.6 Ar 3931 17 Cl 1251.2 K 4419.6 18 Ar 1520.6 Ca 4912.4 Plot the ionization energies versus number of electrons. Explain why the slopes of the I1 and I3 plots are different, even though the species in each row of the table have the same electron configurations.
-
Would you expect the third ionization energy of iron, corresponding to the removal of an electron from a gaseous Fe2+ ion, to be larger or smaller than the fourth ionization energy, corresponding to removal of an electron from a gaseous Fe3+ ion? Why? How would these ionization energies compare to the first ionization energy of Ca?
-
Which would you expect to have the highest first ionization energy: Mg, Al, or Si? Which would you expect to have the highest third ionization energy. Why?
-
Use the values of the first ionization energies given in Figure 3.3.3 to construct plots of first ionization energy versus atomic number for (a) boron through oxygen in the second period; and (b) oxygen through tellurium in group 16. Which plot shows more variation? Explain the reason for the variation in first ionization energies for this group of elements.
-
Arrange Ga, In, and Zn in order of increasing first ionization energies. Would the order be the same for second and third ionization energies? Explain your reasoning.
-
Arrange each set of elements in order of increasing magnitude of electron affinity.
- Pb, Bi, and Te
- Na, K, and Rb
- P, C, and Ge
-
Arrange each set of elements in order of decreasing magnitude of electron affinity.
- As, Bi, and N
- O, F, and Ar
- Cs, Ba, and Rb
-
Of the species F, O−, Al3+, and Li+, which has the highest electron affinity? Explain your reasoning.
-
Of the species O−, N2−, Hg2+, and H+, which has the highest electron affinity? Which has the lowest electron affinity? Justify your answers.
-
The Mulliken electronegativity of element A is 542 kJ/mol. If the electron affinity of A is −72 kJ/mol, what is the first ionization energy of element A? Use the data in the following table as a guideline to decide if A is a metal, a nonmetal, or a semimetal. If 1 g of A contains 4.85 × 1021 molecules, what is the identity of element A?
Na Al Si S Cl EA (kJ/mol) −59.6 −41.8 −134.1 −200.4 −348.6 I (kJ/mol) 495.8 577.5 786.5 999.6 1251.2 -
Based on their valence electron configurations, classify the following elements as either electrical insulators, electrical conductors, or substances with intermediate conductivity: S, Ba, Fe, Al, Te, Be, O, C, P, Sc, W, Na, B, and Rb.
-
Using the data in Problem 10, what conclusions can you draw with regard to the relationship between electronegativity and electrical properties? Estimate the approximate electronegativity of a pure element that is very dense, lustrous, and malleable.
Answers
-
The general features of both plots are roughly the same, with a small peak at 12 electrons and an essentially level region from 15–16 electrons. The slope of the I3 plot is about twice as large as the slope of the I1 plot, however, because the I3 values correspond to removing an electron from an ion with a +2 charge rather than a neutral atom. The greater charge increases the effect of the steady rise in effective nuclear charge across the row.
-
-
Electron configurations: Mg, 1s22s22p63s2; Al, 1s22s22p63s23p1; Si, 1s22s22p63s23p2; First ionization energies increase across the row due to a steady increase in effective nuclear charge; thus, Si has the highest first ionization energy. The third ionization energy corresponds to removal of a 3s electron for Al and Si, but for Mg it involves removing a 2p electron from a filled inner shell; consequently, the third ionization energy of Mg is the highest.
-
-
-
-
- Bi > As > N
- F > O >> Ar
- Rb > Cs > Ba
-
-
Hg2+ > H+ > O− > N2−; Hg2+ has the highest positive charge plus a relatively low energy vacant set of orbitals (the 6p subshell) to accommodate an added electron, giving it the greatest electron affinity; N2− has a greater negative charge than O−, so electron–electron repulsions will cause its electron affinity to be even lower (more negative) than that of O−.
-
-
insulators: S, O, C (diamond), P; conductors: Ba, Fe, Al, C (graphite), Be, Sc, W, Na, Rb; Te and B are semimetals and semiconductors.
-
-
-
-
-
Contributors
- Anonymous
Modified by Joshua Halpern, Scott Sinex and Scott Johnson