2.1.3: Heat and its measurements
- Last updated
- Save as PDF
- Page ID
- 419251
Heat
Heat is energy in transfer to and from a thermodynamic system by a mechanism other than the work or the transfer of matter.
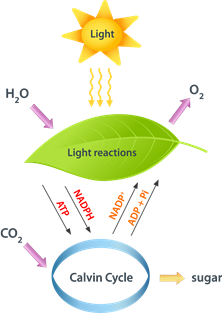
Energy exists in different forms, but energy transforms from one form to another through work or heat. In chemical reactions, a significant portion of energy transfer happens through heat. Green leaves in plants trap the energy from light and store it as chemical energy in the form of glucose synthesized from water and carbon dioxide, as illustrated in Fig. 1.8.1.
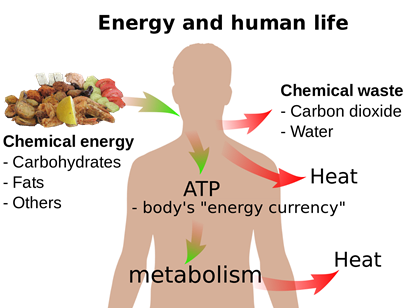
A reverse process happens when we eat food, i.e., the food substances are converted to carbon dioxide, water, and energy, as illustrated in Fig. 1.8.2. Some energy is used to maintain our body temperature at an average level. Another portion is used to drive chemical reactions that consume energy and synthesize substances we need.
Body Temperature
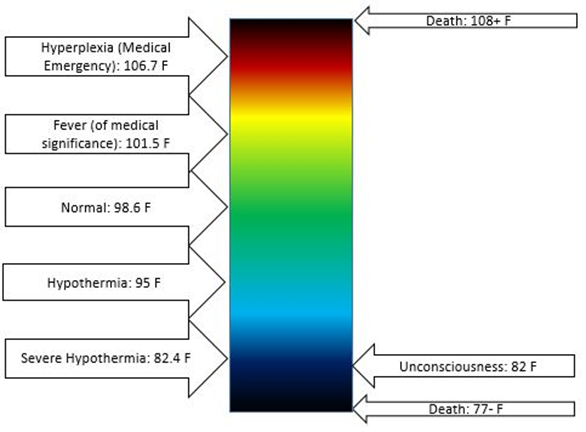
The human body continually loses energy as heat to the environment. The heat released by exothermic reactions in the food digestion process supplies the heat needed to maintain the body temperature at an average level. Human body temperature varies over a small range, as illustrated in Fig. 1.8.3. Hypothermia is <35.0 °C (95.0 °F), normal body temperate is 36.5–37.5 °C (97.7–99.5 °F), fever and hyperthermia is >37.5 or 38.3 °C (99.5 or 100.9 °F), Hyperpyrexia is >40.0 or 41.0 °C (104.0 or 105.8 °F).
Measurement of heat
Temperature is a manifestation of the thermal energy of an object, but the temperature and the energy are not the same. Temperature is a measure of hotness or coldness, and it is intensive, and energy is an extensive physical property of matter. For example, 1 g of water has some energy, but 2 g of water at the same temperature has twice the energy.
Specific heat
The calory (c or cal) is a non-SI unit of heat, work, and energy.
The calory (c or cal)
The energy needed to raise the temperature of 1 g of water by 1 oC is 1 calory
The heat needed to raise the temperature of 2 g of water by 1 oC is 2 calory, and to raise the temperature of 2 g of water by 2 oC is 4 calory. That is, heat energy (q) is directly proportional to both the mass (m) and change in temperature (∆T) of an object:
\begin{equation}
q \propto m \Delta T\nonumber
\end{equation}
Introducing a constant of proportionality, i.e., specific heat (Cs) changes the proportionality to equality, that is known as the heat equation:
\begin{equation}
q=C_{s} m \Delta T\nonumber
\end{equation}
, where Cs is Specific heat.
Specific heat of a substance
The heat energy needed to raise the temperature of 1g of a substance by 1 oC (or 1K) is specific heat if the substance.
The mathematical form of the definition of specific heat is:
\begin{equation}
C_{S}=\frac{q}{m \Delta T}\nonumber
\end{equation}
The units of specific heat are \(\frac{c a l}{g .^{\circ} \mathrm{C}}\), where cal is a non-SI unit of energy. The SI unit of energy is the joule (J). The following is an exact relationship between calory and joule:
\begin{equation}
1 \mathrm{~cal}=4.184 \mathrm{~J} \text { (exact) }\nonumber
\end{equation}
So, the specific heat (Cs) in SI units is: \(\frac{J}{g \cdot^{o} C}\)
The energy unit in nutrition and food is food calory or Calory (C) that is written with capital C, and it is equal to 1000 cal, i.e.,
\begin{equation}
\mathrm{C}=1000 \mathrm{~cal}=1 \mathrm{~kcal}=4184 \mathrm{~J}\nonumber
\end{equation}
, where the capital letter C is food calory.
The specific heat is a characteristic physical property of a material. It varies because the energies of vibrational motions of bonds and other motions that contribute to the thermal energy content differ from material to material. Table 1 lists specific heats of some familiar materials.
Water has higher specific heat than other materials, i.e., it absorbs or releases more heat for the same change in temperature. The environmental temperature variation remains moderate in coastal areas because the temperature change of water is less for the same amount of energy absorbed or released. Note that the specific heat of liquid water is different from solid water (ice) and gaseous water (steam).
| Substance | Specific heat (\(\frac{J}{g \cdot^{o} C}\)) |
|---|---|
| Al | 0.902 |
| C (graphite) | 0.720 |
| Fe | 0.451 |
| Cu | 0.385 |
| Au | 0.128 |
| NH3 (ammonia) | 4.70 |
| H2O (liquid) | 4.184 |
| H2O (ice) | 2.06 |
| H2O(steam) | 2.00 |
| C2H5OH (l) (ethanol) | 2.46 |
| (CH2OH)2 (l) (ethylene glycol, antifreeze) | 2.42 |
| CCl4 (carbon tetrachloride) | 0.861 |
| Wood | 1.76 |
| Concrete | 0.88 |
| Glass | 0.84 |
Calculations using specific heat
The specific heat values are used in the heat equation (\(q=C_{s} m \Delta T\)) to calculate the temperature change for a given amount of heat or the heat energy needed for a given temperature change of a material. A coffee cup calorimeter illustrated in Fig. 1.8.4 is commonly used. It consists of a coffee cup with a lid. It contains water in which the hot or cold object is immersed, or a chemical reaction is performed for heat exchange with the water. A wire loop is used to stir the water. A thermometer records the change in the temperature of the water. The heat absorbed or released by the water is calculated from the data of mass, specific heat, and temperature change of the water.

Example \(\PageIndex{1}\)
Immersing a hot object in 50.0 grams of water in a coffee cup calorimeter increased the water temperature from 22.0 oC to 28.8 oC. How much heat is gained or lost by water?
Solution
Given: m = 50.0 g water, Cs = 4.184 (\frac{J}{g \cdot^{o} C}\), ∆T = Tf – Ti = 28.8 oC – 22.0 oC = 6.8 oC, Desired: heat gained or lost by water, i.e, qwater = ?
Calculations:
\begin{equation}
\mathrm{q}_{\text {water }}=\mathrm{C}_{\mathrm{s}} \mathrm{m} \Delta \mathrm{T}=4.184 \frac{\mathrm{J}}{\mathrm{g}{ }^{\circ} \mathrm{C}} \times 50.0 \mathrm{~g} \times 6.8^{\circ} \mathrm{C}=+1400 \mathrm{~J}\nonumber
\end{equation}
The +ve sign tells water gained 1400 J heat.
Example \(\PageIndex{2}\)
Ammonium nitrate (NH4NO3) is used as a cold pack in hospitals to decrease the temperature of a targeted skin area. When 3.21 g of NH4NO3 is dissolved in 50.0 g of water in a coffee cup calorimeter at 25.0 oC, the temperature decreases to 20.4 oC. What is the amount of heat absorbed or released by water?
Solution
Given: m of solution = 50.0g H2O + 3.21 g NH3NO3 = 53.2 g, Cs = 4.184 (\frac{J}{g \cdot^{o} C}\), ∆T = Tf – Ti =20.4 oC - 25.0 oC = -4.6 oC, Desired: heat gained or lost by the solution, i.e, qsolution = ?
Calculations:
\begin{equation}
\mathrm{q}_{\text {solution }}=\mathrm{C}_{\mathrm{s}} \mathrm{m} \Delta \mathrm{T}=4.184 \frac{\mathrm{J}}{g^{\circ} \mathrm{C}} \times 53.2 \mathrm{~g} \times\left(-4.6^{\circ} \mathrm{C}\right)=-1.0 \times 10^{3} \mathrm{~J}\nonumber
\end{equation}
The –ve sign tells water lost heat
Note
In the problems involving the heating of solution, the mass of solution includes the mass of water and the solute. It is assumed that the specific heat and density of the dilute solution are the same as that of pure water.
Example \(\PageIndex{3}\)
Calcium chloride (CaCl2) is used as a hot pack, i.e., to raise the temperature of a targeted portion of the skin. When CaCl2 dissolves in water, heat is released by the process and absorbed by the surrounding water, increasing the temperature of the water.
When 5.00 g of CaCl2 is dissolved in 50.0 g of water at 23oC in a coffee cup calorimeter, the temperature rises to 39.2oC. What is the amount of heat absorbed or released by water?
Solution
Given: m of solution = 50.0g H2O + 5.00 g CaCl2 = 55.0 g, Cs = 4.184 (\frac{J}{g \cdot^{o} C}\), ∆T = Tf – Ti =39.2 oC - 23.0 oC = 16.2 oC, Desired: heat gained or lost by the solution, i.e, qsolution = ?
Calculations:
\begin{equation}
\mathrm{q}_{\text {solution }}=\mathrm{C}_{\mathrm{s}} \mathrm{m} \Delta \mathrm{T}=4.184 \frac{\mathrm{J}}{g .^{\circ} \mathrm{C}} \times 55.0 \mathrm{~g} \times\left(16.2^{\circ} \mathrm{C}\right)=3.7 \times 10^{3} \mathrm{~J}\nonumber
\end{equation}
The +ve sign tells water gained heat.
The energy released from foods
Foods and fossil fuels are carbon and hydrogen compounds and may also contain some other elements like oxygen, nitrogen, phosphorous, and sulfur. Fuels are used in combustion reactions to release heat for different purposes. The same combustion reactions happen in living systems in several steps to get energy from the foods. For example, the chemical equation for the combustion of glucose is:
\[\ce{C6H12O6 (s) + 6O2 (g) -> 6CO2 (g) + 6H2O (l)}\quad\Delta \mathrm{H}^{\circ}=-2803 \mathrm{~kJ}\nonumber\]
, where ∆Ho is the enthalpy of reaction, i.e., the heat evolved or absorbed at constant pressure conditions. This reaction releases 2803 kJ of energy as heat per mole of glucose. The –ve sign of ∆Ho tells that the reaction releases the energy, i.e., the reaction is exothermic. The same amount of energy is released when glucose is digested and converted to the same products in the living system under the same conditions.
Measurement of energy released from food
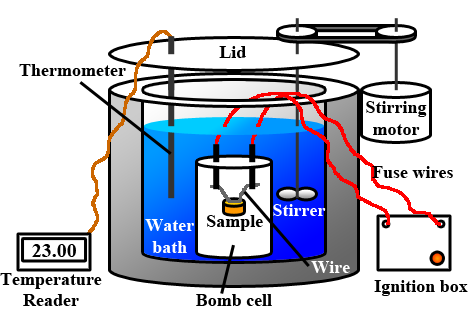
The heat released from the combustion of a substance is measured using a bomb calorimeter illustrated in Fig. 1.8.5. The substance is placed in a particular cell surrounded by an excess of oxygen. An electric spark ignites the substance, and the heat released causes a temperature increase in the water and the other materials in the meter. The heat capacity (Ccp), i.e., the product of the meter's average specific heat and mass and the water components, is calibrated before the experiment. The heat released from the given amount of the substance is calculated from the heat capacity and the measured temperate increase.
Fuel value
The heat of combustion per g of a food is called the fuel value of the food
Glucose is one of the carbohydrates. Carbohydrates are food components that are compounds of carbon, hydrogen, and oxygen in which the ratio of hydrogen-to-oxygen is 2-to-1. The average fuel value of carbohydrates is 17 kJ/g.
The second major class of food is fat. For example, the chemical equation of tristearin C57H110O6, which is a fat, is:
\[\ce{2C57H110O6 (s) + 16O2 (g) -> 114CO2 (g) + 110H2O (l)}\quad\Delta \mathrm{H}^{\circ}=-71609 \mathrm{~kJ}\nonumber\]
The –ve sign with energy value tells the energy is released, or the reaction is exothermic. The average fuel value of fats is 38 kJ/g.
The third primary type of food is protein. Protein is mainly used as a building material in living systems, but it is also used as a source of energy. The average fuel value of protein is 17 kJ/g.
The average fuel values of the three major food components are listed in Table 2. These values are used to calculate the fule value of food servings, as explained in the following examples.
| Food | Fuel value kJ/g |
|---|---|
| Carbohydrates | 17 |
| Proteins | 17 |
| Fats | 38 |
Example \(\PageIndex{1}\)
Calculate the energy released from one cup of orange juice that contains 26 g of carbohydrates, no fat, and 2 g of protein.
Solution
Carbohydrate: \(26 \mathrm{~g} \times 17 \mathrm{~kJ} / \mathrm{g}=442 \mathrm{~kJ}\)
Protein: \(\quad\ 2 \mathrm{~g} \times 17 \mathrm{~kJ} / \mathrm{g}=34 \mathrm{~kJ}\)
Total energy released \(\quad\quad=476 \mathrm{~kJ}\)
The energy value in kJ can be converted to food calories (C) by using the conversion factor based on the following relations.
\begin{equation}
\text { Food calory C }=1000 \mathrm{~cal}=1 \mathrm{~kcal}=4184 \mathrm{~J}\nonumber
\end{equation}


