Template:HideTOC
These are homework exercises to accompany the Textmap created for Chemistry: A Molecular Approach by Nivaldo Tro. Complementary General Chemistry question banks can be found for other Textmaps and can be accessed here. In addition to these publicly available questions, access to private problems bank for use in exams and homework is available to faculty only on an individual basis; please contact Delmar Larsen for an account with access permission.
Q5.38
What volume does 41.2 g of sodium gas at a pressure of 6.9 atm and a temperature of 514 K occupy? Would the volume be different if the sample were 41.2 g of calcium (under identical conditions)?
Strategy
- Know the equation of Ideal Gas Law.
- Rewrite the equation to V=nRT/P
- Write down all of the known data with units.
- Find out the atomic mass.
- Transfer grams to mols.
- Put all numbers into the equation and calculate.
Hints
- PV=nRT, so V=nRT/P
- Mol= mass/ atomic mass
Solution
Based on \(PV=nRT\), and we need to know V, so the equation is rearranged to \(V= nRT/P\).
- R = 0.08206 L (atm)/K (mol).
- P = 6.9 atm.
- T = 514 K
Then, the atomic mass of Sodium =22.99 g/mol
\[n = 41.2 \;g = \dfrac{mass}{atomic\; mass} = \dfrac{41.2\;g}{22.99\; g/mol} = 1.79\; mol\]
Finally, put every number into the equation
\[V=\dfrac{nRT}{P}=\dfrac{(1.79\;mol)(0.0820\;6L (atm)/(K mol))(514\;K}{6.9\; atm} = 10.94\; L\]
Because Calcium has different atomic mass than Sodium, so the volume is different.
Q5.40
We have a 20.0 L cylinder that is filled with 28.6 g of oxygen gas at the temperature of 401 K. What is the pressure that the oxygen gas is exerting on the cylinder?
What we know:
- Molar mass of O2= 32 g/mol
- Temperature is 401 K
- There is 28.6 g of Oxygen
- The volume is 20.0 L
What its asking for: The pressure of the gas
Strategy
- Find an equation that goes with what information you are given
- plug in the information into the formula and get your answer
Solution
Molar mass of O2= 32 g/mol
Moles of O2 in 28.6 g= 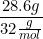 = 0.894 mol O2
= 0.894 mol O2
PV=nRT
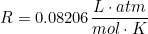
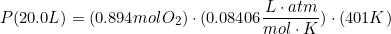
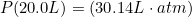
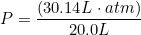
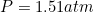
Q5.43
A car tire has a maximum rating of 37.0 psi (gauge pressure). While at the temperature of \(11.0^{\circ}C\), the tire is inflated to a volume of 10.4 L and a gauge pressure of 31.0 psi. When driving on a hot day, the tire warms to \(62.0^{\circ}C\) and its volume expands to 10.9 L. Does the pressure in the tire exceed its maximum rating on the hot day? Note: Gauge pressure is defined as the absolute pressure minutes the atmospheric pressure (14.7 psi).
Solution
- Ideal Gas Law \( PV=nRT\)
- P=pressure, V=volume, n=number of moles, R=gas constant, T=temperature
What we know
- Cold tire: gauge pressure (31.0 psi), volume (10.4 L), temperature (\(11^{\circ}C\))
- Hot tire: volume (10.9), temperature (\(62^{\circ}C\))
- Both- gas constant (\(0.082057\dfrac{L\cdot atm}{mol\cdot K}\))
What we need to find:
- Number of moles (same amount in cold and hot tire)
- Pressure in the hot tire
Strategy
- Convert gauge pressure to total pressure (must be total pressure for Ideal Gas Law). Convert total pressure from psi to atm. Convert temperature from Celsius to Kelvin. Keep volume in L.
- Find the number of moles in the cold tire by using the Ideal Gas Law equation. \[n=\dfrac{PV}{RT}\]
- Find the pressure of the hot tire by plugging in the number of moles found in part B.
- Convert the total pressure to gauge pressure.
- Determine if the pressure exceeds its maximum rating.
Solution
A.
Cold tire:
Gauge pressure=total pressure-atmospheric pressure
31.0 psi= X -14.7 psi
X= 45.7 psi
\[P=45.7 psi\cdot \dfrac{1 atm}{14.7 psi}=3.11 atm\]
\[T=11^{\circ}C+273= 284 K\]
V=10.4 L
\[R=0.082057\dfrac{L\cdot atm}{mol\cdot K}\]
Hot tire:
\[T=62^{\circ}C+273= 335 K\]
V=10.9 L
\[R=0.082057\dfrac{L\cdot atm}{mol\cdot K}\]
B.
\[n=\dfrac{3.11 atm\cdot 10.4 L}{0.082057\dfrac{L\cdot atm}{mol\cdot K}\cdot 284 K}\]
n= 1.39 mol
C.
\[P=\dfrac{1.39 mol\cdot 0.082057\dfrac{L\cdot atm}{mol\cdot K}\cdot 335 K}{10.9 L}\]
P= 3.51 atm
D.
\[3.51 atm\cdot \dfrac{14.7 psi}{1 atm}= 51.6 psi\]
51.6 psi-14.7 psi= 36.9 psi
The gauge pressure is 36.9 psi and since the maximum rating is 37.0 psi, the pressure does not exceed the maximum rating (although close).
Q5.44
A balloon is floating on top of an ocean at a volume of 2.04 L at a pressure of 730 mmHg and a temperature at 20 °C. A sea creature then gets hungry and pulls the balloon down to the bottom of the ocean where the temperature decreases to 5°C while the pressure increases to 1510 mmHg. Suppose the balloon can freely increase, calculate the volume of the balloon.
Strategy
- Figure out which formula corresponds with the Ideal Gas Law
- Write down everything that is given to you in the problem
- Convert If you need to
- Solve for what you're looking for
Solution
Step 1. Equation for Ideal Gas Law:
\[PV=nRT\]
- \(P\): Pressure
- \(V\): Volume
- \(n\): Moles
- \(R\): Ideal Gas Constant (0.08206 atm. mol / (L K)
- \(T\): Temperature
Step 2. What do we know ?


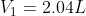
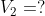
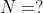
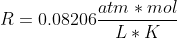


Step 3. Convert. The first thing we need to do is to convert the Pressure and the Temperature.
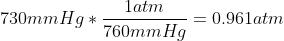
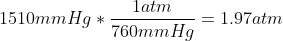


Step 4. The next thing we need to do is find \(n\) and cancel out units.
 --------->
---------> 
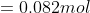
Step 5. Now that we have found our moles, we can now plug it into our equation to find the volume. Don't forget to cancel out your units.
\[PV - nRT \rightarrow V = \dfrac{nRT}{P} = 0.950\;L\]
Answer
\[V_2 =0.950\;L\]
Q5.55
Calculate the density of Ne gas at 143 ºC and 4.3 atm.
What we know
- Pressure (4.3 atm),
- temperature (143 ºC ),
- the identity of the gas (Ne),
- the molar mass of Ne from the periodic table (20.2 g/mol).
Asked for
- Density (\(\rho\)) of Ne under specific pressure and temperature conditions
Strategy:
- The temperature is given in degrees Celsius, which must be converted to Kelvin.
- Solve for the density. \[\rho = \dfrac{mass}{volume}\]
Solution:
A Calculate Temperature in Kelvin:
\[T = 143\; ºC + 273 = 416\; K\]
B Calculate the density of Ne
\[\rho = \dfrac{MM \cdot P}{RT}\]
\[\rho = \dfrac{\rm 20.2 g/mol \cdot 4.3 \rm atm}{(0.08206 \dfrac{\rm L atm}{\rm mol K}) \rm 416 K}\]
\[\rho= \rm 2.54 g/L\]
Q.11.56
Determine the volume in liters occupied by 64.5 grams of Argon at STP.
Hint
- Use the molar volume of a gas at STP to help determine the answer.
Strategy
- Determine the molar volume using the condition of standard temperature and pressure, or STP. The standard temperature is 273 K and the standard pressure is 1 atm. We need to determine what formula would be best for the problem.
- After we figure out the formula to use for this problem, we need to figure out what numbers to plug in. We already know the standard temperature of pressure of a gas which are the letters P and T. We are trying to find V, so that leaves us to figure out n and R.
- Last, we plug in the numbers we have found and work out the equation to determine the volume.
Solution
A. The formula to use to determine the molar volume for this problem is \(PV=nRT\).
B. Since we know the numbers to plug in for P and T, we need to find numbers for \(n\) and \(R\). The rate, R, is \(0.08206 \dfrac{L\cdot atm}{mol\cdot K}\). This will always be the R for this equation. To determine n, the number of moles, we must use what is given to us, which is the grams or Ar.mol of
\[Ar= 64.5\; g \;of \;Ar \cdot \dfrac{1 \;mol\; of\; Ar}{39.948\; g \;of \;Ar} =1.61 \;mol\; of Ar\]
C. Now, we have all the numbers except the one we are looking for, which is V. Plug them in and work out the equation.
\[1 atm\cdot V=1.61 mol of Ar \cdot 0.08206 \dfrac{L\cdot atm}{mol\cdot K} \cdot 273 K\]
Q5.61
What is the total pressure in (atm) of a mixture of gases in a closed container with the partial pressures as indicated: H, 115 torr; Ar, 105 torr; and N2, 204 torr? What is the mass of H, Ar, and N2 at 28°C and 1.45 L?
Solution and Strategy
- Find total pressure of the system by adding all of the partial pressures. \[115\; torr +105\;torr+204\;torr=total pressure\]\[424\;torr=total pressure\]
- Convert total pressure to atmospheres through dimensional analysis. \[\left(\dfrac{424torr}{1}\right) \times \left(\dfrac{1atm}{760\;torr})\right)=0.558atm\]
- Now we must try and find the masses of each of the substances, to do this we must first find the fractional pressures, and convert them to atmospheres by multiplying by the total pressure.
\[H=(\dfrac{115\;torr}{424\;torr})=0.2712\]
\[Ar=(\dfrac{105\;torr}{424\;torr})=0.2476\]
\[N_{2}=(\dfrac{204\;torr}{424\;torr})=0.4811\]
- Next we multiply by the total pressure to get our fractional pressures in atmospheres.
\[H=(0.2712)(0.558\;atm)=0.151\;atm\]
\[Ar=(0.2476)(0.558\;atm)=0.138\;atm\]
\[N_{2}=(0.4811)(0.558\;atm)=0.268\;atm\]
- Before we plug in our numbers we must find the volume for each element, to do this we multiply our fractional pressures by the total volume.
\[H=(0.2712)(1.45\;L)=0.393L\]
\[Ar=(0.2476)(1.45\;L)=0.359L\]
\[N_2=(0.4811)(1.45\;L)=0.698L\]
- The final step before we can use our equation is to convert our temperature from Celsius to Kelvin. \[28 °C + 273 = 30\;1K\]
- Now we must utilize the equation \[PV=nRT, where P=pressure(atm), V=volume(L), n=moles, R=.0821\dfrac{L*atm}{mol*K}, T=Temperature(K))\] to find mole of the substance. We modify this equation to give us. \[n=\dfrac{PV}{RT}\]
- Now we use this equation to find our moles of each gas.
\[n(H)=\dfrac{(0.151atm)(0.393L)}{(0.0821\dfrac{L*atm}{mol*K})(301K)}=0.0024mol\]
\[n(Ar)=\dfrac{(0.138atm)(0.359L)}{(0.0821\dfrac{L*atm}{mol*K})(301K)}=0.0020mol\]
\[n(N_{2})=\dfrac{(0.268atm)(0.698L)}{(0.0821\dfrac{L*atm}{mol*K})(301K)}=0.0076mol\]
- Now that we have the moles we must multiply this by the molar mass of each gas to find its value in grams.
\[H=(0.0024mol)(1.008\dfrac{g}{mol})=0.0024g\]
\[Ar=(0.0020mol)(39.95\dfrac{g}{mol})=0.0799g\]
\[N_{2}=(0.0076mol)(28.02\dfrac{g}{mol})=0.2130g\]
Answer:
\[Total Pressure=0.558atm\] \[H=0.0024g\] \[Ar=0.0799g\] \[N_{2}=0.2130g\]
Q5.67a
Hydrogen gas produced by a chemical reaction is collected in the vapor space of a container holding water. The hydrogen partial pressure is 605 mmHg and the system temperature is 55 °C. What is the total pressure in the container? If 0.1 mole of H2 was produced in the reaction, what is the total volume of the gas above the water in the container in L? Use the gas constant R of 62.3637 \[\dfrac{L\cdot mmHg}{mol\cdot K}\]
Solution
Answer, Part 1
Knowing the system temperature is 55 °C, the vapor pressure of the water in the hydrogen/water vapor mixture can be determined. Using Table 11.3 on page 412, the water partial pressure is found to be 118.2 mmHg.
From Equation 11.8 we know that
\[P_{Total} = P_{H_2O} + P_{H_2}\]
PH2 is given as 605 mmHg and PH2O was found to be 118.2 mmHg
PTotal = 605 mmHg + 118.2 mmHg = 723.2 mmHg
Answer, Part 2
It is given there is 0.1 mole of H2 and hydrogen partial pressure 605 mmHg. In the first part of this problem, the total system pressure was found to be 723.2 mmHg.
Solving Equation 11.10 for the total number of moles, we find \[n_{total}=\left ( \dfrac{n_{H_{2}}}{P_{H_{2}}} \right )\cdot P_{total}\]
Therefore
\[n_{total}=\left ( \dfrac{0.1 mol_{H_{2}}}{605mmHg_} \right )\cdot 723.2 mmHg_=0.12 mol\]
From the Ideal Gas Law, we know \(PV=n_{total}RT\)
Solving for V, we find
\[V=n_{total}\left ( \dfrac{RT}{P} \right )\]
Convert the system temperature to Kelvin. K = 55 °C + 273.2 = 328.2 K
Therefore V is:
\[V=0.12mol\left ( \dfrac{62.3637\dfrac{L\cdot mmHg}{mol\cdot K}\cdot 328.2K}{723.2mmHg} \right )=3.4L\]
Q5.67b
Hydrogen gas is collected over water at 35 °C at a total pressure of 745 mmHg. What is the partial pressure of the hydrogen gas collected? Given that the total volume of the gas collected is 750 ml, calculate the mass of the hydrogen gas collected.

