7.4: Counting Molecules by the Gram

Last updated
Save as PDF

Page ID: 105308

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

Learning Objectives

Define molecular mass and formula mass.
Perform conversions between mass and number of particles.

Molecular and Formula Masses

The molecular mass of a substance is the sum of the average masses of the atoms in one molecule of a substance. It is calculated by adding together the atomic masses of the elements in the substance, each multiplied by its subscript (written or implied) in the molecular formula. Because the units of atomic mass are atomic mass units, the units of molecular mass are also atomic mass units. The procedure for calculating molecular masses is illustrated in Example \(\PageIndex{1}\).

Example \(\PageIndex{1}\): Ethanol

Calculate the molecular mass of ethanol, whose condensed structural formula is \(CH_3CH_2OH\). Among its many uses, ethanol is a fuel for internal combustion engines

Solution

Steps for Problem Solving
Identify the "given"information and what the problem is asking you to "find."	Given: Ethanol molecule (CH₃CH₂OH) Find: molecular mass
Determine the number of atoms of each element in the molecule.	The molecular formula of ethanol may be written in three different ways: CH₃CH₂OH (which illustrates the presence of an ethyl group CH₃CH₂₋, and an −OH group) C₂H₅OH, and C₂H₆O; All show that ethanol has two carbon atoms, six hydrogen atoms, and one oxygen atom.
Obtain the atomic masses of each element from the periodic table and multiply the atomic mass of each element by the number of atoms of that element.	1 C atom = 12.011 amu 1 H atom = 1.0079 amu 1 O atom = 15.9994 amu
Add together the masses to give the molecular mass.	2C: (2atoms)(12.011amu/atom) = 24.022 amu 6H: (6atoms)(1.0079amu/atom) = 6.0474amu +1O: (1atoms)(15.9994amu/atom) =15.9994amu C₂H₆O : molecular mass of ethanol = 46.069amu

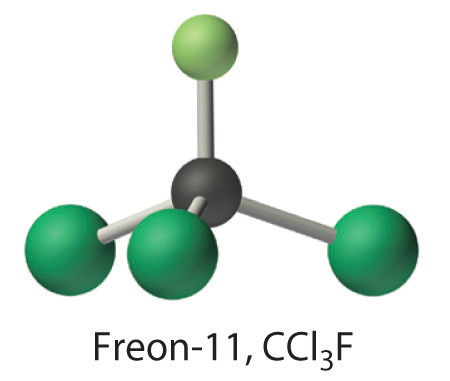
Exercise \(\PageIndex{1}\): Freon

Calculate the molecular mass of trichlorofluoromethane, also known as Freon-11, whose condensed structural formula is CCl₃F. Until recently, it was used as a refrigerant. The structure of a molecule of Freon-11 is as follows:

Answer:: 137.37 amu

Unlike molecules, which form covalent bonds, ionic compounds do not have a readily identifiable molecular unit. Therefore, for ionic compounds, the formula mass (also called the empirical formula mass) of the compound is used instead of the molecular mass. The formula mass is the sum of the atomic masses of all the elements in the empirical formula, each multiplied by its subscript (written or implied). It is directly analogous to the molecular mass of a covalent compound. The units are atomic mass units.

Atomic mass, molecular mass, and formula mass all have the same units: atomic mass units.

Example \(\PageIndex{2}\): Calcium Phosphate

Calculate the formula mass of Ca₃(PO₄)₂, commonly called calcium phosphate. This compound is the principal source of calcium found in bovine milk.

Solution

Steps for Problem Solving
Identify the "given"information and what the problem is asking you to "find."	Given: Calcium phosphate [Ca₃(PO₄)₂] formula unit Find: formula mass
Determine the number of atoms of each element in the molecule.	The empirical formula—Ca₃(PO₄)₂—indicates that the simplest electrically neutral unit of calcium phosphate contains three Ca²⁺ ions and two PO₄³⁻ ions. The formula mass of this molecular unit is calculated by adding together the atomic masses of three calcium atoms, two phosphorus atoms, and eight oxygen atoms.
Obtain the atomic masses of each element from the periodic table and multiply the atomic mass of each element by the number of atoms of that element.	1 Ca atom = 40.078 amu 1 P atom = 30.973761 amu 1 O atom = 15.9994 amu
Add together the masses to give the formula mass.	3Ca: (3 atoms) (40.078 amu/atom)=120.234amu 2P: (2 atoms) (30.973761amu/atom)=61.947522amu + 8O: (8 atoms)(15.9994amu/atom)=127.9952amu Formula mass of Ca₃(PO₄)₂=310.177amu

Exercise \(\PageIndex{2}\): Silicon Nitride

Calculate the formula mass of Si₃N₄, commonly called silicon nitride. It is an extremely hard and inert material that is used to make cutting tools for machining hard metal alloys.

\(Si_3N_4\) bearing parts. (Public Domain; David W. Richerson and Douglas W. Freitag; Oak Ridge National Laboratory).

Answer:: 140.29 amu

Molar Mass

The molar mass of a substance is defined as the mass in grams of 1 mole of that substance. One mole of isotopically pure carbon-12 has a mass of 12 g. For an element, the molar mass is the mass of 1 mol of atoms of that element; for a covalent molecular compound, it is the mass of 1 mol of molecules of that compound; for an ionic compound, it is the mass of 1 mol of formula units. That is, the molar mass of a substance is the mass (in grams per mole) of 6.022 × 10²³ atoms, molecules, or formula units of that substance. In each case, the number of grams in 1 mol is the same as the number of atomic mass units that describe the atomic mass, the molecular mass, or the formula mass, respectively.

The molar mass of any substance is its atomic mass, molecular mass, or formula mass in grams per mole.

The periodic table lists the atomic mass of carbon as 12.011 amu; the average molar mass of carbon—the mass of 6.022 × 10²³ carbon atoms—is therefore 12.011 g/mol:

**Table \(\PageIndex{1}\):** Molar Mass of Select Substances
Substance (formula)	Basic Unit	Atomic, Molecular, or Formula Mass (amu)	Molar Mass (g/mol)
carbon (C)	atom	12.011 (atomic mass)	12.011
ethanol (C₂H₅OH)	molecule	46.069 (molecular mass)	46.069
calcium phosphate [Ca₃(PO₄)₂]	formula unit	310.177 (formula mass)	310.177

Converting Between Grams and Moles of a Compound

The molar mass of any substance is the mass in grams of one mole of representative particles of that substance. The representative particles can be atoms, molecules, or formula units of ionic compounds. This relationship is frequently used in the laboratory. Suppose that for a certain experiment you need 3.00 moles of calcium chloride \(\left( \ce{CaCl_2} \right)\). Since calcium chloride is a solid, it would be convenient to use a balance to measure the mass that is needed. Dimensional analysis will allow you to calculate the mass of \(\ce{CaCl_2}\) that you should measure as show in Example \(\PageIndex{3}\).

Example \(\PageIndex{3}\): Calcium Chloride

Calculate the mass of 3.00 moles of calcium chloride (CaCl₂).

CK12 Screenshot 10-4-1.png

Calcium chloride is used as a drying agent and as a road deicer.

Solution

Steps for Problem Solving
Identify the "given"information and what the problem is asking you to "find."	Given: 3.00 moles of CaCl₂ Find: g CaCl₂
List other known quantities	1 ml CaCl₂ = 110.98 g CaCl₂
Prepare a concept map and use the proper conversion factor.
Cancel units and calculate.	\(3.00 \: \cancel{\text{mol} \: \ce{CaCl_2}} \times \dfrac{110.98 \: \text{g} \: \ce{CaCl_2}}{1 \: \cancel{\text{mol} \: \ce{CaCl_2}}} = 333 \: \text{g} \: \ce{CaCl_2}\)
Think about your result.

Exercise \(\PageIndex{3}\): Calcium Oxide

What is the mass of \(7.50 \: \text{mol}\) of (calcium oxide) \(\ce{CaO}\)?

Answer:: 420.60 g

Example \(\PageIndex{4}\): Water

How many moles are present in 108 grams of water?

Solution

Steps for Problem Solving
Identify the "given"information and what the problem is asking you to "find."	Given: 108 g H₂O Find: mol H₂O
List other known quantities	\(1 \: \text{mol} \: \ce{H_2O} = 18.02 \: \text{g}\) H₂O
Prepare a concept map and use the proper conversion factor.
Cancel units and calculate.	\(108 \: \cancel{\text{g} \: \ce{H_2O}} \times \dfrac{1 \: \text{mol} \: \ce{H_2O}}{18.02 \: \cancel{\text{g} \: \ce{H_2O}}} = 5.99 \: \text{mol} \: \ce{H_2O}\)
Think about your result.

Exercise \(\PageIndex{4}\): Nitrogen Gas

What is the mass of \(7.50 \: \text{mol}\) of Nitrogen gas \(\ce{N2}\)?

Answer:: 105 g

Conversions Between Mass and Number of Particles

In "Conversions Between Moles and Mass", you learned how to convert back and forth between moles and the number of representative particles. Now you have seen how to convert back and forth between moles and mass of a substance in grams. We can combine the two types of problems into one. Mass and number of particles are both related to moles. To convert from mass to number of particles or vice-versa, it will first require a conversion to moles as shown in Figure \(\PageIndex{1}\) and Example \(\PageIndex{5}\).

6.4.PNG — Figure \(\PageIndex{1}\): *Conversion from number of particles to mass or from mass to number of particles requires two steps.*

Example \(\PageIndex{5}\): Chlorine

How many molecules is \(20.0 \: \text{g}\) of chlorine gas, \(\ce{Cl_2}\)?

Solution

Steps for Problem Solving
Identify the "given"information and what the problem is asking you to "find."	Given: 20.0 g Cl₂ Find: # Cl₂molecules
List other known quantities	1 mol Cl₂ = 70.90 g Cl₂, 1mol Cl₂ = 6.022 x 10²³ Cl₂molecules
Prepare a concept map and use the proper conversion factor.
Cancel units and calculate.	\(20.0 \: \cancel{\text{g} \: \ce{Cl_2}} \times \dfrac{1 \: \cancel{\text{mol} \: \ce{Cl_2}}}{70.90 \: \cancel{\text{g} \: \ce{Cl_2}}} \times \dfrac{6.02 \times 10^{23} \: \text{molecules} \: \ce{Cl_2}}{1 \: \cancel{\text{mol} \: \ce{Cl_2}}} = 1.70 \times 10^{23} \: \text{molecules} \: \ce{Cl_2}\)
Think about your result.	Since the given mass is less than half of the molar mass of chlorine, the resulting number of molecules is less than half of Avogadro's number.

Exercise \(\PageIndex{5}\): Calcium Chloride

How many formula units are in 25.0 g of CaCl₂ ?

Answer:: 1.36 x 10²³ CaCl₂ formula units

Summary

Calculations for formula mass and molecular mass are described.
Calculations involving conversions between moles of a material and the mass of that material are described.
Calculations are illustrated for conversions between mass and number of particles.

Contributors and Attributions

Marisa Alviar-Agnew (Sacramento City College)
Henry Agnew (UC Davis)

Search

Text Color

Text Size

Margin Size

Font Type