9.1: The Born-Oppenheimer Approximation Simplifies the Schrödinger Equation for Molecules
- Page ID
- 210852
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Using quantum mechanics to predict the chemical bonding patterns, optimal geometries, and physical and chemical properties of molecules is a large and active field of research known as molecular quantum mechanics or more commonly as quantum chemistry. The density functional theory referred to in the previous lecture, for which the chemistry Nobel prize was given in 1998, has had a tremendous impact in quantum chemistry, with some of the papers in this subject having acquired some 10,000 citations each since their publication. In fact, the 1998 chemistry Nobel prize was shared between Walter Kohn, one of the inventors of density functional theory and John Pople, the developer of a commonly used quantum chemistry software package.
Quantum chemistry calculations allow the geometries of molecules to be computed as well as a wide range of properties. Quantum chemistry can also be used in a novel way, in which the electrons are treated using quantum mechanics but the nuclei are treated as classical particles. We use quantum mechanics to calculate the internuclear forces but then use these forces in Newton's Second Law to study the motion of the nuclei during chemical reactions. This gives us a microscopic window into the specific motions, the complex dance, executed by the nuclei during a simple or complex chemical process.
The methods of quantum chemistry have become very sophisticated, and there are various software packages that can be downloaded for carrying out the calculations of quantum chemistry. It should be noted that these packages use a series of approximations to solve the Schrödinger equation because for all but the simplest of molecules, exact solutions are not available. We will discuss some of these methods, but first we need to introduce some of the underlying theory.
The Born-Oppenheimer Approximation
The Born-Oppenheimer approximation is one of the basic concepts underlying the description of the quantum states of molecules. This approximation makes it possible to separate the motion of the nuclei and the motion of the electrons. This is not a new idea for us. We already made use of this approximation in the particle-in-a-box model when we explained the electronic absorption spectra of cyanine dyes without considering the motion of the nuclei. Then we discussed the translational, rotational and vibrational motion of the nuclei without including the motion of the electrons. In this chapter we will examine more closely the significance and consequences of this important approximation. Note, in this discussion nuclear refers to the atomic nuclei as parts of molecules not to the internal structure of the nucleus.
The Born-Oppenheimer approximation neglects the motion of the atomic nuclei when describing the electrons in a molecule. The physical basis for the Born-Oppenheimer approximation is the fact that the mass of an atomic nucleus in a molecule is much larger than the mass of an electron (more than 1000 times). Because of this difference, the nuclei move much more slowly than the electrons. In addition, due to their opposite charges, there is a mutual attractive force of \(Ze^2/r^2\) acting on an atomic nucleus and an electron. This force causes both particles to be accelerated. Since the magnitude of the acceleration is inversely proportional to the mass, a = F/m, the acceleration of the electrons is large and the acceleration of the atomic nuclei is small; the difference is a factor of more than 2000. Consequently, the electrons are moving and responding to forces very quickly, and the nuclei are not. You can imagine running a 100-yard dash against someone whose acceleration is a 2000 times greater than yours. That person could literally run circles around you.
If two particles interact in some way, and one is much heavier than the other, the light particle will move essentially as a "slave'' of the heavy particle. That is, it will simply follow the heavy particle wherever it goes, and, it will move rapidly in response to the heavy particle motion. As an illustration of this phenomenon, consider the simple mechanical system pictured below:
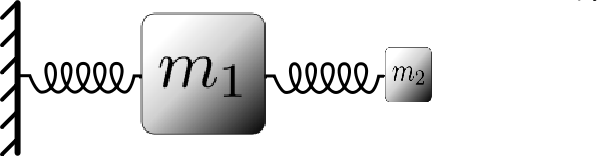
Considering this as a classical system, we expect that the motion will be dominated by the large heavy particle (\(m_1\)), which is attached to a fixed wall by a spring. The small, light particle (\(m_2\), which is attached to the heavy particle by a spring will simply follow the heavy particle and execute rapid oscillations around it.
So a good approximation is to describe the electronic states of a molecule by thinking that the nuclei are not moving, i.e. that they are stationary. The nuclei, however, can be stationary at different positions so the electronic wavefunction can depend on the positions of the nuclei even though their motion is neglected.
Now we look at the mathematics to see what is done in solving the Schrödinger equation after making the Born-Oppenheimer approximation. For a diatomic molecule as an example, the Hamiltonian operator is grouped into three terms
\[\hat {H} (r, R) = \hat {T}_{nuc} (R) + \dfrac {e^2}{4\pi \epsilon _0} \dfrac {Z_A Z_B}{R} + \hat {H} _{elec} (r,R) \label {9.1.1}\]
where
\[\hat{T}_{nuc} (R) = -\dfrac {\hbar^2}{2m_A} \nabla ^2_A - \dfrac {\hbar ^2}{2m_B} \nabla ^2_B \label {9.1.2}\]
and
\[\hat {H} _{elec} (\vec{r}, \vec{R}) = \dfrac {- \hbar ^2}{2m} \sum \limits _i \nabla ^2_i + \dfrac {e^2}{4 \pi \epsilon _0} \left ( -\sum \limits _i \dfrac {Z_A}{r_{Ai}} - \sum \limits _i \dfrac {Z_B}{r_{Bi}} + \dfrac {1}{2} \sum \limits _i \sum \limits _{j \ne i} \dfrac {1}{r_{ij}}\right ) \label{9.1.3}\]
In Equation \ref{9.1.1}, the first term represents the kinetic energy of the nuclei, the second term represents the Coulomb repulsion of the two nuclei, and the third term represents the contribution to the energy from the electrons, which consists of their kinetic energy, mutual repulsion for each other, and attraction for the nuclei. \(\vec{r}\) and \(\vec{R}\) are vectors specifying the positions of all the electrons and all the nuclei, respectively.
Define all the symbols in Equations \ref{9.1.1} through \ref{9.1.3}.
- Answer
-
\begin{align*}
\hat{H}(r,R) &= \underbrace{\hat{T}_{nuc}(R)}_\text{Kinetic Energy Term for nuclei} + \underbrace{\frac{e^2}{4\pi\epsilon_o}\frac{Z_AZ_B}{R}}_\text{Repulsion Term for nuclei} + \underbrace{\hat{H}_{elec}(r,R)}_\text{Hamiltonian for electrons}\\
\hat{T}_{nuc}(R) &= \underbrace{\frac{\hslash^2}{2m_A}\nabla^2_A}_\text{Kinetic Energy Term for nuclei A} - \underbrace{\frac{\hslash^2}{2m_b}\nabla^2_B}_\text{Kinetic Energy Term for nuclei B}\\
\hat{H}_{elec}(\vec{r},\vec{R}) &= \underbrace{\frac{-\hslash^2}{2m}\sum_{i}\nabla_i^2}_\text{Kinetic Energy Term for electrons} + \frac{e^2}{4\pi\epsilon_o}\left(-\underbrace{\sum_{i}\frac{Z_A}{r_{Ai}}}_\text{Attraction Term between nuclei A and electron i} - \underbrace{\sum_{i}\frac{Z_B}{R_{Bi}}}_\text{Attraction Term between nuclei B and electron i} + \underbrace{\frac{1}{2}\sum_{i}\sum_{j \neq i}\frac{1}{r_{ij}}}_\text{Repulsion Term between electrons}\right)
\end{align*}where, \(Z_x \)is the charge of particle x, \(m_x\) is the mass of particle x and \(r_{xz}\) is the distance between particle x and z.
Explain why the factor of 1/2 appears in the last term in Equation \ref{9.1.3}.
- Answer
-
The 1/2 term is there to make sure we do not double count the potential energies via the two summations. Otherwise, we would independently add the potential energy of electron 1 with electron 2 and the potential energy of electron 2 with electron 1. These are the same and hence one has to be removed.
The Born-Oppenheimer approximation says that the nuclear kinetic energy terms in the complete Hamiltonian, Equation \ref{9.1.1}, can be neglected in solving for the electronic wavefunctions and energies. Consequently, the electronic wavefunction \(\varphi _e (r,R)\) is found as a solution to the electronic Schrödinger equation
\[\hat {H} _{elec} (r, R) \varphi _e (r, R) = E_e (R) \varphi _e (r, R) \label {9.1.4}\]
Even though the nuclear kinetic energy terms are neglected, the Born-Oppenheimer approximation still takes into account the variation in the positions of the nuclei in determining the electronic energy and the resulting electronic wavefunction depends upon the nuclear positions, \(R\). As a result of the Born-Oppenheimer approximation, the molecular wavefunction can be written as a product
\[\psi _{ne} (r, R) = X_{ne} (R) \varphi _e (r, R) \label {9.1.5}\]
This product wavefunction is called the Born-Oppenheimer wavefunction. The function \(X_{ne} (R)\) is the vibrational wavefunction, which is a function of the nuclear coordinates \(R\) and depends upon both the vibrational and electronic quantum numbers or states, n and e, respectively. The electronic function, \(\varphi _e (r, R) \), is a function of both the nuclear and electronic coordinates, but only depends upon the electronic quantum number or electronic state, e. Translational and rotational motion is not included here. The translational and rotational wavefunctions simply multiply the vibrational and electronic functions in Equation \ref{9.1.5} to give the complete molecular wavefunction when the translational and rotational motions are not coupled to the vibrational and electronic motion.
In the Crude Born-Oppenheimer Approximation, \(R\) is set equal to \(R_o\), the equilibrium separation of the nuclei, and the electronic wavefunctions are taken to be the same for all positions of the nuclei (i.e., the nuclei never move). The electronic energy, \(E_e (R)\), in Equation \ref{9.1.4} combines with the repulsive Coulomb energy of the two nuclei, to form the potential energy function that controls the nuclear motion as shown in Figure \(\PageIndex{1}\).
\[ V_e (R) = E_e (R) + \dfrac {e^2}{4\pi \epsilon _0} \dfrac {Z_A Z_B}{R} \label {9.1.6}\]
Consequently the Schrödinger equation for the vibrational motion is
\[( \hat {T} _{nuc} (R) + V (R) ) X_{ne} (R) = E_{ne} X_{ne} (R) \label {9.1.7}\]
Potential Energy Curves and Surfaces
Previously, the potential energy was approximated as a harmonic potential or Morse potential depending on the displacement, \(R\), of the nuclei from their equilibrium positions.
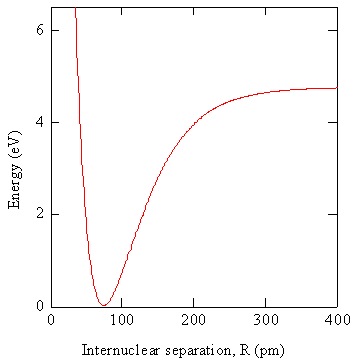
In practice the electronic Schrödinger equation is solved using approximations at particular values of \(R\) to obtain the wavefunctions \(\varphi _e (r,R)\) and potential energies \(V_e (R)\). The potential energies can be graphed as illustrated in Figure \(\PageIndex{1}\).
The graph in Figure \(\PageIndex{1}\) is the energy of a diatomic molecule as a function of internuclear separation, which serves as the potential energy function for the nuclei. When R is very large there are two atoms that are weakly interacting. As \(R\) becomes smaller, the interaction becomes stronger, the energy becomes a large negative value, and we say a bond is formed between the atoms. At very small values of \(R\), the internuclear repulsion is very large so the energy is large and positive. This energy function controls the motion of the nuclei. Previously, we approximated this function by a harmonic potential to obtain the description of vibrational motion in terms of the harmonic oscillator model. Other approximate functional forms could be used as well, e.g. the Morse potential. The equilibrium position of the nuclei is where this function is a minimum, i.e. at \(R = R_0\). If we obtain the wavefunction at \(R = R_0\) and use this function for all values of \(R\), we have employed the Crude Born-Oppenheimer approximation.
Relate Equation \ref{9.1.7} to the one previously used in our description of molecular vibrations in terms of the harmonic oscillator model.
While the potential energy function, \(V_e (R)\), for a diatomic molecule is a 1-D curve (Figure \(\PageIndex{1}\)), molecules with more than two atoms will have multi-dimensional potential energy surfaces with 3N-6 (or 3N-5 for linear molecule) dimensions for the number of internal degrees of freedom.
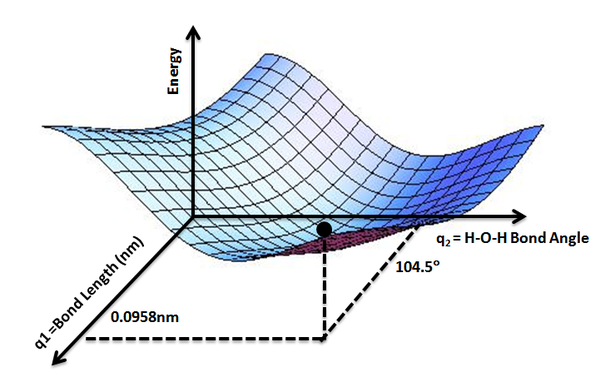
The potential energy surface concept can be used to theoretically explore properties of structures composed of atoms, for example, finding the minimum energy shape of a molecule or computing the rates of a chemical reaction. Qualitatively the reaction coordinate diagrams (one-dimensional slices through the potential energy surfaces) have numerous applications. Chemists use reaction coordinate diagrams as both an analytical and pedagogical aid for rationalizing and illustrating kinetic and thermodynamic events. The purpose of energy profiles and surfaces is to provide a qualitative representation of how potential energy varies with molecular motion for a given reaction or process.
Explain the difference between the Born-Oppenheimer approximation and the Crude Born-Oppenheimer approximation.
Summary
In this section we started with the Schrödinger equation for a diatomic molecule and separated it into two equations, an electronic Schrödinger equation and a nuclear Schrödinger equation. In order to make the separation, we had to make an approximation. We had to neglect the effect of the nuclear kinetic energy on the electrons. The fact that this assumption works can be traced to the fact that the nuclear masses are much larger than the electron mass. We then used the solution of the electronic Schrödinger equation to provide the potential energy function for the nuclear motion. The solution to the nuclear Schrödinger equation provides the vibrational wavefunctions and energies.
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski ("Quantum States of Atoms and Molecules")

