1.5: The Rydberg Formula and the Hydrogen Atomic Spectrum
- Page ID
- 210779
- Describe Rydberg's theory for the hydrogen spectra.
- Interpret the hydrogen spectrum in terms of the energy states of electrons.
In an amazing demonstration of mathematical insight, in 1885 Balmer came up with a simple formula for predicting the wavelength of any of the lines in atomic hydrogen in what we now know as the Balmer series. Three years later, Rydberg generalized this so that it was possible to determine the wavelengths of any of the lines in the hydrogen emission spectrum. Rydberg suggested that all atomic spectra formed families with this pattern (he was unaware of Balmer's work). It turns out that there are families of spectra following Rydberg's pattern, notably in the alkali metals, sodium, potassium, etc., but not with the precision the hydrogen atom lines fit the Balmer formula, and low values of \(n_2\) predicted wavelengths that deviate considerably.
Rydberg's phenomenological equation is as follows:
\[ \begin{align} \widetilde{\nu} &= \dfrac{1}{ \lambda} \\[4pt] &=R_H \left( \dfrac{1}{n_1^2} -\dfrac{1}{n_2^2}\right) \label{1.5.1} \end{align} \]
where \(R_H\) is the Rydberg constant and is equal to 109,737 cm-1 and \(n_1\) and \(n_2\) are integers (whole numbers) with \(n_2 > n_1\).
For the Balmer lines, \(n_1 =2\) and \(n_2\) can be any whole number between 3 and infinity. The various combinations of numbers that can be substituted into this formula allow the calculation the wavelength of any of the lines in the hydrogen emission spectrum; there is close agreement between the wavelengths generated by this formula and those observed in a real spectrum.
Other Series
The results given by Balmer and Rydberg for the spectrum in the visible region of the electromagnetic radiation start with \(n_2 = 3\), and \(n_1=2\). Is there a different series with the following formula (e.g., \(n_1=1\))?
\[\dfrac{1}{\lambda} = R_{\textrm H} \left(\dfrac{1}{1^2} - \dfrac{1}{n^2} \right ) \label{1.5.2}\]
The values for \(n_2\) and wavenumber \(\widetilde{\nu}\) for this series would be:
| \(n_2\) | 2 | 3 | 4 | 5 | ... |
|---|---|---|---|---|---|
| \(\lambda\) (nm) | 121 | 102 | 97 | 94 | ... |
| \(\widetilde{\nu}\) (cm-1) | 82,2291 | 97,530 | 102,864 | 105,332 | ... |
Do you know in what region of the electromagnetic radiation these lines are? Of course, these lines are in the UV region, and they are not visible, but they are detected by instruments; these lines form a Lyman series. The existences of the Lyman series and Balmer's series suggest the existence of more series. For example, the series with \(n_2 = 3\) and \(n_1\) = 4, 5, 6, 7, ... is called Pashen series.
The spectral lines are grouped into series according to \(n_1\) values. Lines are named sequentially starting from the longest wavelength/lowest frequency of the series, using Greek letters within each series. For example, the (\(n_1=1/n_2=2\)) line is called "Lyman-alpha" (Ly-α), while the (\(n_1=3/n_2=7\)) line is called "Paschen-delta" (Pa-δ). The first six series have specific names:
- Lyman series with \(n_1 = 1\)
- Balmer series with \(n_1 = 2\)
- Paschen series (or Bohr series) with \(n_1 = 3\)
- Brackett series with \(n_1 = 4\)
- Pfund series with \(n_1 = 5\)
- Humphreys series with \(n_1 = 6\)
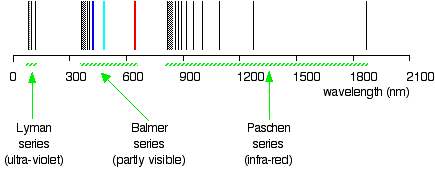
The so-called Lyman series of lines in the emission spectrum of hydrogen corresponds to transitions from various excited states to the n = 1 orbit. Calculate the wavelength of the lowest-energy line in the Lyman series to three significant figures. In what region of the electromagnetic spectrum does it occur?
Given: lowest-energy orbit in the Lyman series
Asked for: wavelength of the lowest-energy Lyman line and corresponding region of the spectrum
Strategy:
- Substitute the appropriate values into Equation \(\ref{1.5.1}\) (the Rydberg equation) and solve for \(\lambda\).
- Locate the region of the electromagnetic spectrum corresponding to the calculated wavelength.
Solution:
We can use the Rydberg equation (Equation \ref{1.5.1}) to calculate the wavelength:
\[ \dfrac{1}{\lambda }=R_H \left ( \dfrac{1}{n_{1}^{2}} - \dfrac{1}{n_{2}^{2}}\right ) \nonumber \]
A For the Lyman series, \(n_1 = 1\).
\[ \begin{align*} \dfrac{1}{\lambda } &=R_H \left ( \dfrac{1}{n_{1}^{2}} - \dfrac{1}{n_{2}^{2}}\right ) \\[4pt] &=1.097 \times 10^{7}\, m^{-1}\left ( \dfrac{1}{1}-\dfrac{1}{4} \right )\\[4pt] &= 8.228 \times 10^{6}\; m^{-1} \end{align*} \]
Spectroscopists often talk about energy and frequency as equivalent. The cm-1 unit (wavenumbers) is particularly convenient. We can convert the answer in part A to cm-1.
\[ \begin{align*} \widetilde{\nu} &=\dfrac{1}{\lambda } \\[4pt] &= 8.228\times 10^{6}\cancel{m^{-1}}\left (\dfrac{\cancel{m}}{100\;cm} \right ) \\[4pt] &= 82,280\: cm^{-1} \end{align*} \]
and
\[\lambda = 1.215 \times 10^{−7}\; m = 122\; nm \nonumber \]
This emission line is called Lyman alpha and is the strongest atomic emission line from the sun and drives the chemistry of the upper atmosphere of all the planets producing ions by stripping electrons from atoms and molecules. It is completely absorbed by oxygen in the upper stratosphere, dissociating O2 molecules to O atoms which react with other O2 molecules to form stratospheric ozone
B This wavelength is in the ultraviolet region of the spectrum.
The Pfund series of lines in the emission spectrum of hydrogen corresponds to transitions from higher excited states to the \(n_1 = 5\). Calculate the wavelength of the second line in the Pfund series to three significant figures. In which region of the spectrum does it lie?
- Answer
-
\(4.65 \times 10^3\, nm\); infrared
The above discussion presents only a phenomenological description of hydrogen emission lines and fails to provide a probe of the nature of the atom itself. Clearly a continuum model based on classical mechanics is not applicable, and as the next Section demonstrates, a simple connection between spectra and atomic structure can be formulated.
Contributors
Michael Fowler (Beams Professor, Department of Physics, University of Virginia)
Chung (Peter) Chieh (Professor Emeritus, Chemistry @ University of Waterloo)