9.6: Allosteric Interactions

Skills to Develop

• When a substrate binds to one enzymatic subunit, the rest of the subunits are stimulated and become active. Ligands can either have non-cooperativity, positive cooperativity or negative cooperativity.

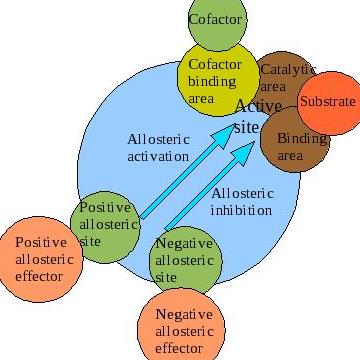
A significant portion of enzymes function such that their properties can be studied using the Michaelis-Menten equation. However, a particular class of enzymes exhibit kinetic properties that cannot be studied using the Michaelis-Menten equation. The rate equation of these unique enzymes is characterized by an “S-shaped” sigmoidal curve, which is different from the majority of enzymes whose rate equation exhibits hyberbolic curves. Allosteric regulation is the regulation of an enzyme or other protein by binding an effector molecule at the protein's allosteric site (that is, a site other than the protein's active site). Effectors that enhance the protein's activity are referred to as allosteric activators, whereas those that decrease the protein's activity are called allosteric inhibitors. The term allostery refers to the fact that the regulatory site of an allosteric protein is physically distinct from its active site. Allosteric regulations are a natural example of control loops, such as feedback from downstream products or feedforward from upstream substrates. Long-range allostery is especially important in cell signaling.

Allosteric Modulation (Cooperativity)

Cooperativity is a phenomenon displayed by enzymes or receptors that have multiple binding sites where the affinity of the binding sites for a ligand is increased, positive cooperativity, or decreased, negative cooperativity, upon the binding of a ligand to a binding site. We also see cooperativity in large chain molecules made of many identical (or nearly identical) subunits (such as DNA, proteins, and phospholipids), when such molecules undergo phase transitions such as melting, unfolding or unwinding. This is referred to as subunit cooperativity (discussed below).

An example of positive cooperativity is the binding of oxygen to hemoglobin. One oxygen molecule can bind to the ferrous iron of a heme molecule in each of the four chains of a hemoglobin molecule. Deoxy-hemoglobin has a relatively low affinity for oxygen, but when one molecule binds to a single heme, the oxygen affinity increases, allowing the second molecule to bind more easily, and the third and fourth even more easily. The oxygen affinity of 3-oxy-hemoglobin is ~300 times greater than that of deoxy-hemoglobin. This behavior leads the affinity curve of hemoglobin to be sigmoidal, rather than hyperbolic as with the monomeric myoglobin. By the same process, the ability for hemoglobin to lose oxygen increases as fewer oxygen molecules are bound.

Negative allosteric modulation (also known as allosteric inhibition) occurs when the binding of one ligand decreases the affinity for substrate at other active sites. For example, when 2,3-BPG binds to an allosteric site on hemoglobin, the affinity for oxygen of all subunits decreases. This is when a regulator is absent from the binding site.

Another instance in which negative allosteric modulation can be seen is between ATP and the enzyme Phosphofructokinase within the negative feedback loop that regulates glycolysis. Phosphofructokinase (generally referred to as PFK) is an enzyme that catalyses the third step of glycolysis: the phosphorylation of Fructose-6-phosphate into Fructose 1,6-bisphosphate. PFK can be allosterically inhibited by high levels of ATP within the cell. When ATP levels are high, ATP will bind to an allosteric site on phosphofructokinase, causing a change in the enzyme's three-dimensional shape. This change causes its affinity for substrate (fructose-6-phosphate and ATP) at the active site to decrease, and the enzyme is deemed inactive. This causes glycolysis to cease when ATP levels are high, thus conserving the body's glucose and maintaining balanced levels of cellular ATP. In this way, ATP serves as a negative allosteric modulator for PFK, despite the fact that it is also a substrate of the enzyme.

Sigmoidal kinetic profiles are the result of enzymes that demonstrate positive cooperative binding. cooperativity refers to the observation that binding of the substrate or ligand at one binding site affects the affinity of other sites for their substrates. For enzymatic reactions with multiple substrate binding sites, this increased affinity for the substrate causes a rapid and coordinated increase in the velocity of the reaction at higher \([S]\) until \(V_{max}\) is achieved. Plotting the \(V_0\) vs. \([S]\) for a cooperative enzyme, we observe the characteristic sigmoidal shape with low enzyme activity at low substrate concentration and a rapid and immediate increase in enzyme activity to \(V_{max}\) as \([S]\) increases. The phenomenon of cooperativity was initially observed in the oxygen-hemoglobin interaction that functions in carrying oxygen in blood. Positive cooperativity implies allosteric binding – binding of the ligand at one site increases the enzyme’s affinity for another ligand at a site different from the other site. Enzymes that demonstrate cooperativity are defined as allosteric. There are several types of allosteric interactions: homotropic (positive) and heterotropic (negative).

.
Figure 1: Rate of Reaction (velocity) vs. Substrate Concentration.

Positive and negative allosteric interactions (as illustrated through the phenomenon of cooperativity) refer to the enzyme's binding affinity for other ligands at other sites, as a result of ligand binding at the initial binding site. When the ligands interacting are all the same compounds, the effect of the allosteric interaction is considered homotropic. When the ligands interacting are different, the effect of the allosteric interaction is considered heterotropic. It is also very important to remember that allosteric interactions tend to be driven by ATP hydrolysis.

The Hill Equation

The degree of cooperativity is determined by Hill equation (Equation \(\ref{Eq1}\)) for non-Michaelis-Menten kinetics. The Hill equation accounts for allosteric binding at sites other than the active site. \(n\) is the "Hill coefficient."

\[ \theta = \dfrac{[L]^n}{K_d+[L]^n} = \dfrac{[L]^n}{K_a^n+[L]^n} \label{Eq1}\]

where

• \( \theta \) is the fraction of ligand binding sites filled
• \([L]\) is the ligand concentration
• \(K_d\) is the apparent dissociation constant derived from the law of mass action (equilibrium constant for dissociation)
• \(K_a\) is the ligand concentration producing half occupation (ligand concentration occupying half of the binding sides), that is also the microscopic dissociation constant
• \(n\) is the Hill coefficient that describes the cooperativity

Taking the logarithm of both sides of the equation leads to an alternative formulation of the Hill Equation.

\[ \log \left( \dfrac{\theta}{1-\theta} \right) = n\log [L] - \log K_d \label{Eq2}\]

• when \(n < 1\), there is negative cooperativity
• when \(n = 1\), there is no cooperativity
• when \(n > 1\), there is positive cooperativity

Allosteric Models

Currently, there are 2 models for illustrating cooperativity: the concerted model and the sequential model. Most allosteric effects can be explained by the concerted MWC model put forth by Monod, Wyman, and Changeux, or by the sequential model described by Koshland, Nemethy, and Filmer. Both postulate that enzyme subunits exist in one of two conformations, tensed (T) or relaxed (R), and that relaxed subunits bind substrate more readily than those in the tense state. The two models differ most in their assumptions about subunit interaction and the preexistence of both states.

The Concerted model

The concerted model of allostery, also referred to as the symmetry model or MWC model, postulates that enzyme subunits are connected in such a way that a conformational change in one subunit is necessarily conferred to all other subunits. Thus, all subunits must exist in the same conformation. The model further holds that, in the absence of any ligand (substrate or otherwise), the equilibrium favours one of the conformational states, T or R. The equilibrium can be shifted to the R or T state through the binding of one ligand (the allosteric effector or ligand) to a site that is different from the active site (the allosteric site).

The Sequential model

The sequential model of allosteric regulation holds that subunits are not connected in such a way that a conformational change in one induces a similar change in the others. Thus, all enzyme subunits do not necessitate the same conformation. Moreover, the sequential model dictates that molecules of substrate bind via an induced fit protocol. In general, when a subunit randomly collides with a molecule of substrate, the active site, in essence, forms a glove around its substrate. While such an induced fit converts a subunit from the tensed state to relaxed state, it does not propagate the conformational change to adjacent subunits. Instead, substrate-binding at one subunit only slightly alters the structure of other subunits so that their binding sites are more receptive to substrate. To summarize:

• subunits need not exist in the same conformation
• molecules of substrate bind via induced-fit protocol
• conformational changes are not propagated to all subunits

Note: Allosteric database

Allostery is a direct and efficient means for regulation of biological macromolecule function, produced by the binding of a ligand at an allosteric site topographically distinct from the orthosteric site. Due to the often high receptor selectivity and lower target-based toxicity, allosteric regulation is also expected to play an increasing role in drug discovery and bioengineering. The AlloSteric Database (ASD, provides a central resource for the display, search and analysis of the structure, function and related annotation for allosteric molecules. Currently, ASD contains allosteric proteins from more than 100 species and modulators in three categories (activators, inhibitors, and regulators). Each protein is annotated with detailed description of allostery, biological process and related diseases, and each modulator with binding affinity, physicochemical properties and therapeutic area. Integrating the information of allosteric proteins in ASD should allow the prediction of allostery for unknown proteins, to be followed with experimental validation. In addition, modulators curated in ASD can be used to investigate potential allosteric targets for a query compound, and can help chemists to implement structure modifications for novel allosteric drug design.

Summary

Allosteric enzymes are an exception to the Michaelis-Menten model. Because they have more than two subunits and active sites, they do not obey the Michaelis-Menten kinetics, but instead have sigmoidal kinetics. Since allosteric enzymes are cooperative, a sigmoidal plot of \(V_0\) versus \([S]\) results: There are distinct properties of Allosteric Enzymes that makes it different compared to other enzymes.

1. One is that allosteric enzymes do not follow the Michaelis-Menten Kinetics. This is because allosteric enzymes have multiple active sites. These multiple active sites exhibit the property of cooperativity, where the binding of one active site affects the affinity of other active sites on the enzyme. As mentioned earlier, it is these other affected active sites that result in a sigmoidal curve for allosteric enzymes.
2. Allosteric Enzymes are influenced by substrate concentration. For example, at high concentrations of substrate, more enzymes are found in the R state. The T state is favorite when there is an insufficient amount of substrate to bind to the enzyme. In other words, the T and R state equilibrium depends on the concentration of the substrate.
3. Allosteric Enzymes are regulated by other molecules. This is seen when the molecules 2,3-BPG, pH, and CO2 modulates the binding affinity of hemoglobin to oxygen. 2,3-BPG reduces binding affinity of O2 to hemoglobin by stabilizing the T- state. Lowering the pH from physiological pH=7.4 to 7.2 (pH in the muscles and tissues) favors the release of \(O_2\). Hemoglobin is more likely to release oxygen in \(CO_2\) rich areas in the body.

There are two primary models for illustrating cooperativity. The concerted model (also called the Monod-Wyman-Changeux model) illustrates cooperativity by assuming that proteins have two or more subunits, and that each part of the protein molecule is able to exist in either the relaxed (R) state or the tense (T) state - the tense state of a protein molecule is favored when it doesn't have any substrates bound. All aspects, including binding and dissociation constants are the same for each ligand at the respective binding sites. The sequential model aims to demonstrate cooperativity by assuming that the enzyme/protein molecule affinity is relative and changes as substrates bind. Unlike the concerted model, the sequential model accounts for different species of the protein molecule.

Contributors

Template:ContribWorldPublicLibrary