Formula and Composition of Water and Glucose
- Page ID
- 152872
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We have presented a microscopic view of the chemical reaction between oxygen and hydrogen. The equation
\[\ce{O2 (g) + 2 H2 (g) -> 2H2O (l)}\]
represents the same event in terms of chemical symbols and formulas.
We also saw that plants form glucose from CO2 and H2O:
\[\ce{6CO2 (g) + 6 H2O (l) + Light Energy -> C6H12O6 (s) + 6O2(g)}\]
But how does a practicing chemist find out what is occurring on the microscopic scale? When a reaction is observed for the first time, little is known about the microscopic nature of the products. It is therefore necessary to determine experimentally the composition and formula of a newly synthesized substance.
The first step in such a procedure is usually to separate and purify the products of a reaction. The products above are easy to separate, because they are liquids or solids, while the reactants are gaseous. But how could you determine that the formula should be H2O, and not H2O2? And plants produce mixtures of carbohydrates during photosynthesis, which must be separated by chromatography or other techniques before they can be identified. Glucose is perhaps the most common simple sugar, and it exists in two molecular forms, with the chemical formula C6H12O6:
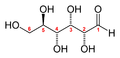
the open chain form of glucose
Plants may produce other simple sugars with similar structures, like D-ribulose (C5H10O5), D-fructose (C6H12O6) and di- or polysaccharides (with two or more simple sugars linked together) like sucrose (C12H22O11) or Maltose(C12H22O11).
One answer involves quantitative analysis—the determination of the percentage by mass of each element in the compound. Such data are usually reported as the percent composition.
Example \(\PageIndex{1}\): Percent Composition
When 10.0 g oxygen reacts with sufficient hydrogen, 11.26 g of a pure compound is formed. Calculate the percent composition from these experimental data.
Solution
The percentage of oxygen is the mass of oxygen divided by the total mass of compound times 100 percent:
\[ \text{%O} = \tfrac {\text{m}_{\text{O}}} {\text{m}_{\text{compound}}} \cdot \text{100%} = \tfrac{\text{10.0 g}} {\text{11.26 g}} \cdot \text{100%} = \text{88.81%}\]
The remainder of the compound (11.26 g – 10 g = 1.26 g) is hydrogen:
\[\text{%H} = \tfrac{\text{m}_{\text{H}}} {\text{m}_{\text{compound}}} \cdot \text{100%} = \tfrac{\text{1.26 g}} {\text{11.26 g}} \cdot \text{100%} = \text{11.19%} \]
As a check, verify that the percentages add to 100:
88.81% + 11.19% = 100%
To obtain the formula from percent-composition data, we must find how many hydrogen atoms there are per oxygen atom. On a macroscopic scale this corresponds to the ratio of the amount of hydrogen to the amount of oxygen. If the formula is H2O, it not only indicates that there are two hydrogen atoms per oxygen atom, it also says that there are 2 mol of hydrogen atoms for each 1 mol of oxygen atoms. That is, the amount of hydrogen is twice the amount of oxygen. The numbers in the ratio of the amount of bromine to the amount of mercury (2:1) are the subscripts of hydrogen and oxygen in the formula.
Example \(\PageIndex{2}\): Formula Determination
Determine the formula for the compound whose percent composition was calculated in the previous example.
Solution
For convenience, assume that we have 100 g of the compound. Of this, 88.81 g (88.81%) is oxygen and 11.19 g is hydrogen. Each mass can be converted to an amount of substance
\begin{align} & n_{\text{O}}=\text{88}\text{.81 g}\times \frac{\text{1 mol O}}{\text{16}\text{.00 g}}=\text{5}\text{.550 mol O} \\ & n_{\text{H}}=\text{11}\text{.19 g}\times \frac{\text{1 mol H}}{\text{1}\text{.008 g}}=\text{11}\text{.101 mol H} \\ \end{align}
So the formula is H11.101O5.550, but we know there are no fractions of atoms, so we have to put this in a standard form. To do this, we divide the larger amount by the smaller:
\[\frac{n_{\text{H} }}{n_ { \text{O} }}=\frac{\text{11.19 mol H}}{\text{5.550 mol O}}=\frac{\text{1.998 mol H}}{\text{1 mol O}}\]
To the formula is H1.998O1, but again, there seems to be a problem. The ratio 1.998 mol H to 1 mol O also implies that there are 1.998 H atoms per 1 O atom. If the atomic theory is correct, there is no such thing as 0.998 atom; but remembering that our mesurements are only good to three significant figures, we round 1.998 to 2.00 and write the formula as H2O.
Example \(\PageIndex{3}\): Formula of Compound
An oxide of hydrogen has the composition 94.07% O and 5.93% H. Find its formula.
Solution
Again assume a 100-g sample and calculate the amount of each element:
\begin{align} & n_{\text{O}}=\text{94}\text{.07 g}\times \frac{\text{1 mol O}}{\text{16}\text{.00 g}}=\text{5}\text{.88 mol O} \\ & n_{\text{H}}=\text{5}\text{.93 g}\times \frac{\text{1 mol H}}{\text{1}\text{.008 g}}=\text{5}\text{.88 mol H} \\ \end{align}
The ratio is
\[\frac{n_{\text{H}}}{n_{\text{O}}}=\frac{\text{5.88 mol H}}{\text{5.88 mol O}}=\frac{\text{1 mol H}}{\text{1 mol O}}\]
So the formula is H5.88O5.88, which is a 1:1 ratio within experimental precision. We would therefore assign the formula HO.
The formula obtained in Example 3 does not correspond to either of the two hydrogen oxides we have already discussed. Is it a third one? The answer is no because our method can only determine the ratio of H to O. The ratio 1:1 is the same as 2:2, and so our method will give the same result for HO or H2O2 (or H7O7, for that matter, should it exist). The formula determined by this method is called the empirical formula or simplest formula. Occasionally, as in the case of hydrogen peroxde, the empirical formula differs from the actual molecular composition, or the molecular formula. Experimental determination of the molecular weight in addition to percent composition permits calculation of the molecular formula.
Example \(\PageIndex{4}\): Empirical and Molecular Formulas
A compound whose molecular weight is 28 contains 85.6% C and 14.4% H. Determine its empirical and molecular formulas.
Solution
\begin{align} & n_{\text{C}}=\text{85}\text{.6 g}\times \frac{\text{1 mol C}}{\text{12}\text{.01 g}}=\text{7}\text{.13 mol C} \\ & n_{\text{H}}=\text{14}\text{.4 g}\times \frac{\text{1 mol H}}{\text{1}\text{.008 g}}=\text{14}\text{.3 mol H} \\ \end{align}
So the formula is C7.13H14.3, but to get integral subscripts we divide each by the smaller: \[\frac{n_{\text{H}}}{n_{\text{C}}}=\frac{\text{14.3 mol H}}{\text{7.13 mol C}}=\frac{\text{2.01 mol H}}{\text{1 mol C}}\]
The empirical formula is therefore CH2. The molecular weight corresponding to the empirical formula is
12.01 + 2 × 1.008 = 14.03
Since the experimental molecular weight is twice as great, all subscripts must be doubled and the molecular formula is C2H4.Example \(\PageIndex{5}\): Empirical Formula
D-Xylose contains 40.0% C, 6.71% H, and 53.29% O. What is its empirical formula?
Solution
\begin{align} & n_{\text{H}}=\text{6}\text{.71 g}\times \tfrac{\text{1 mol H}}{\text{1}\text{.008 g}}=\text{6}\text{.66 mol H} \\ & n_{\text{C}}=\text{40}\text{.00 g}\times \frac{\text{1 mol C}}{\text{12}\text{.01 g}}=\text{3}\text{.33 mol C} \\ & n_{\text{O}}=\text{53}\text{.29 g}\times \frac{\text{1 mol O}}{\text{16}\text{.00 g}}=\text{3}\text{.33 mol O} \\ \end{align}
So the formula is C3.33H6.66O3.33, and dividing all three by the smallest amount of substance we obtain CH2O.
\begin{align} & \frac{n_{\text{C}}}{n_{\text{O}}}=\frac{\text{3}\text{.33 mol C}}{\text{3}\text{.33 mol O}}=\frac{\text{1}\text{. mol H}}{\text{1 mol O}} \\ & \frac{n_{\text{H}}}{n_{\text{O}}}=\frac{\text{4}\text{.44 mol H}}{\text{2}\text{.22 mol O}}=\frac{\text{2}\text{.00 mol H}}{\text{1 mol O}} \\ \end{align}
Now we see where carbohydrates get their name. They all have formulas like Cn(H2O)m, so they all look like hydrates (water containing compounds) of carbon. D-Xylose is actually C5(H2O)5 or C5H10O5, Glucose is C6(H12O)6 or C6H12O6, and Sucrose is C12(H2O)11 or C12H22O11.
We have seen that experimental error can give mole ratios that are not exact units. Occasionally the ratio of amounts is farther from a whole number than can be explained by experimental error, as in the following example.
Example \(\PageIndex{6}\): Empirical Formula of Aspirin
Aspirin contains 60.0% C, 4.48% H, and 35.5% O. What is its empirical formula?
Solution
\begin{align} & n_{\text{H}}=\text{14}\text{.4 g}\times \frac{\text{1 mol H}}{\text{1}\text{.008 g}}=\text{14}\text{.3 mol H} \\ & n_{\text{C}}=\text{85}\text{.6 g}\times \frac{\text{1 mol C}}{\text{12}\text{.01 g}}=\text{7}\text{.13 mol C} \\ & n_{\text{O}}=\text{35}\text{.5 g}\times \frac{\text{1 mol O}}{\text{16}\text{.00 g}}=\text{2}\text{.22 mol O} \\ \end{align}
Divide all three by the smallest amount of substance\begin{align} & \frac{n_{\text{C}}}{n_{\text{O}}}=\frac{\text{5}\text{.00 mol C}}{\text{2}\text{.22 mol O}}=\frac{\text{2}\text{.25 mol H}}{\text{1 mol O}} \\ & \frac{n_{\text{H}}}{n_{\text{O}}}=\frac{\text{4}\text{.44 mol H}}{\text{2}\text{.22 mol O}}=\frac{\text{2}\text{.00 mol H}}{\text{1 mol O}} \\ \end{align}
Clearly there are twice as many H atoms as O atoms, but the ratio of C to O is not so obvious. We must convert 2.25 to a ratio of small whole numbers. This can be done by changing the figures after the decimal point to a fraction. In this case, .25 becomes ¼. Thus 2.25 = 2¼ = 9/4, and\[\frac{n_{\text{C}}}{n_{\text{O}}}=\frac{\text{2.25 mol C}}{\text{1 mol O}}=\frac{\text{9 mol C}}{\text{4 mol O}}\]
We can also write
\[\frac{n_{\text{H}}}{n_{\text{O}}}=\frac{\text{2 mol H}}{\text{1 mol O}}=\frac{\text{8 mol H}}{\text{4 mol O}}\]
Thus the empirical formula is C9H8O4.
Once someone has determined a formula–empirical or molecular—it is possible for someone else to do the reverse calculation. Finding the weight-percent composition from the formula often proves quite informative, as the following example shows.
Example \(\PageIndex{7}\): Percent Composition of a Sugar
As we saw above, all carbohydrates have the general formula Cn(H2O)m. All simple sugars have the general formula Cn(H2O)n, so they all have the same percentage of C, H, and O.
a. Calculate the percent C in glucose. b. Show that the compound C8(H2O)4 cannot be a simple sugar by calculating its percent composition.
Solution
a. C6(H2O)6 contains 6 mol C, 12 mol H, and 6 mol O. The molar mass is thus
M = (6 x 12.011) + (12 x 1.008) + (6 x 16) = 180 g mol–1
A 1-mol sample would weigh 180.56 g. The mass of 6 mol C it contains is
\[\text{mC}=\text{6 mol C}\cdot\frac{\text{12.011 g}}{\text{1 mol C}}=\text{72.066 g}\]
Therefore the percentage of C is\[\text{%C}=\frac{\text{mC}}{\text{mC6H_{12}O_6}}\cdot\text{ 100%}=\frac{\text{72.066 g}}{\text{180.56 g}}\cdot\text{100%}=\text{40.00%}\]
The percentages of H and O are easily calculated as\begin{align} & m_{\text{H}}=\text{12 mol H}\cdot=\frac{\text{1.008 g}}{\text{1 mol H}}=\text{12.096 g}\\&\text{%H}= \frac{\text{12.096 g}}{\text{180.56 g}}\cdot\text{100%}=\text{6.70%}\\& m_{\text{O}}=\text{6 mol O}\cdot=\frac{\text{16.00 g}}{\text{1 mol O}}=\text{96.00 g}\\& \text{%O}= \frac{\text{96.00 g}}{\text{180.56 g}}\cdot\text{100%}=\text{53.17%}\\\end{align}
Though not strictly needed to answer the problem, the latter two percentages provide a check of the results. The total 40.00 + 6.70% + 53.17% = 100.00% as it should.Note that for any simple sugar,
\[\text{%C}=\tfrac{\textit{n}\text{(12.011)}}{\textit{n}\text{(12.011)} +\textit{n}\text{(18)}} = \text{40%}\]
regardless of how many carbons it contains (simple sugars are trioses, C3H6O3, tetroses, C4H8O4, pentoses, and hexoses. The same goes for the percent H and O.
b. The molar mass of C8(H2O)4 is 168.15;
%C = [(8 x 12.011)/168.15] x 100% = 57.14%, not the 40% characteristic of simple sugars.
Similarly,
%H = [(8 x 1.008) / 168.15] x 100% = 4.80% and the percent O is 38.06%.
From ChemPRIME: 2.11: Formulas and Composition
Contributors
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.


