8.3: Volatilization Gravimetry

A second approach to gravimetry is to thermally or chemically decompose the sample and measure the resulting change in its mass. Alternatively, we can trap and weigh a volatile decomposition product. Because the release of a volatile species is an essential part of these methods, we classify them collectively as volatilization gravimetric methods of analysis.

8.3.1 Theory and Practice

Whether an analysis is direct or indirect, volatilization gravimetry usually requires that we know the products of the decomposition reaction. This is rarely a problem for organic compounds, which typically decompose to form simple gases such as CO₂, H₂O, and N₂. For an inorganic compound, however, the products often depend on the decomposition temperature.

Thermogravimetry

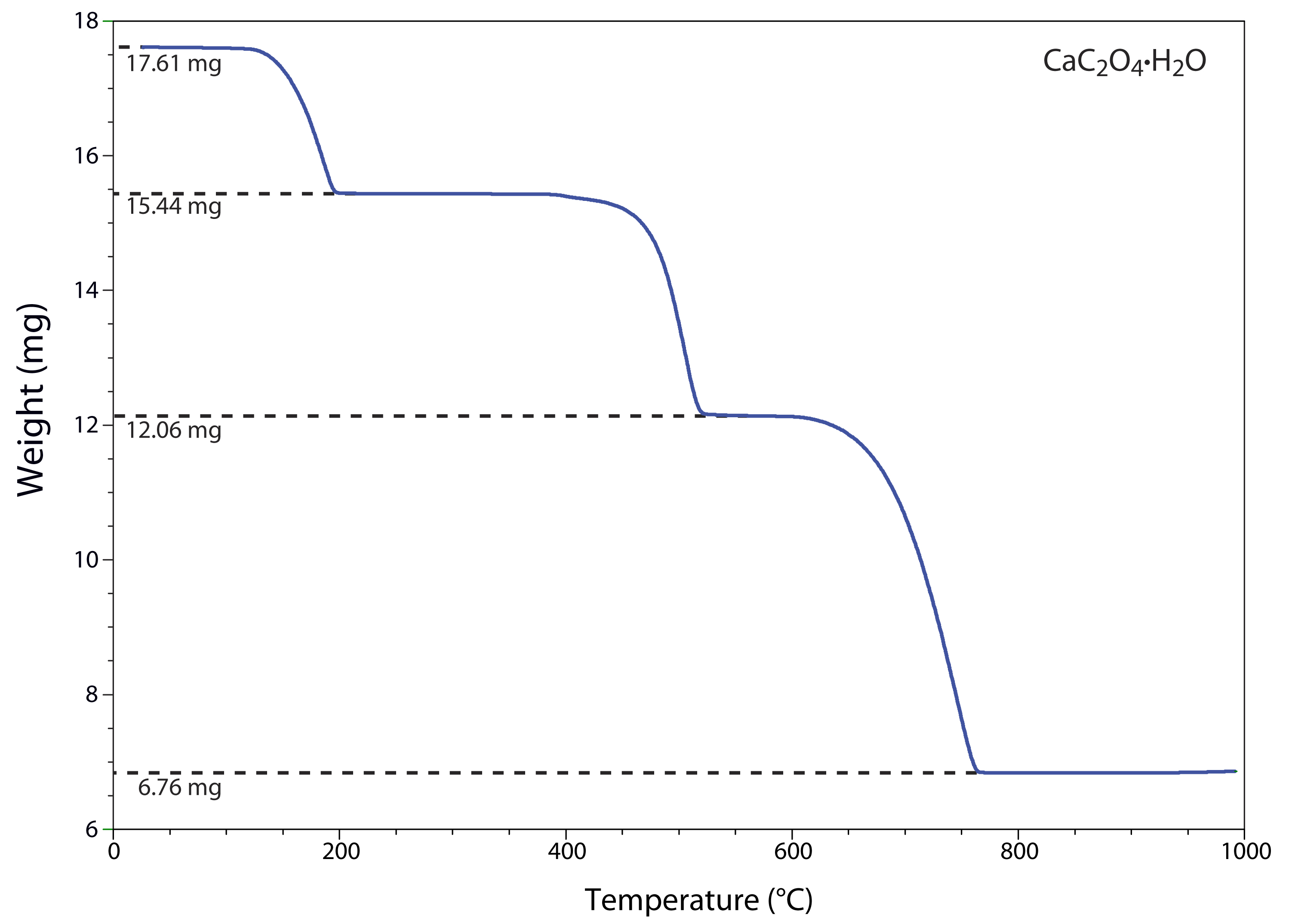
One method for determining the products of a thermal decomposition is to monitor the sample’s mass as a function of temperature, a process called thermogravimetry. Figure 8.10 shows a typical thermogram in which each change in mass—each “step” in the thermogram—represents the loss of a volatile product. As shown in Example 8.4, we can use a thermogram to identify a compound’s decomposition reactions.

Figure 8.10 Thermogram for CaC₂O₄•H₂O obtained by heating a sample from room temperature to 1000^oC at a rate of 20^oC/min. Each change in mass results from the loss of a volatile product. The sample’s initial mass and its mass after each loss are shown by the dotted lines. See Example 8.4 for information on interpreting this thermogram.

Example 8.4

The thermogram in Figure 8.10 shows the mass of a sample of calcium oxalate monohydrate, CaC₂O₄•H₂O, as a function of temperature. The original sample weighing 17.61 mg was heated from room temperature to 1000^oC at a rate of 20^oC per minute. For each step in the thermogram, identify the volatilization product and the solid residue that remains.

Solution

From 100–250^oC the sample loses 17.61 mg – 15.44 mg, or 2.17 mg, which is

\[\mathrm{\dfrac{2.17\;mg}{17.61\;mg}\times100=12.3\%}\]

of the sample’s original mass. In terms of CaC₂O₄•H₂O, this corresponds to a loss of

\[\mathrm{0.123\times146.11\;g/mol=18.0\;g/mol}\]

The product’s molar mass and the temperature range for the decomposition, suggest that this is a loss of H₂O(g), leaving a residue of CaC₂O₄.

The loss of 3.38 mg from 350–550^oC is a 19.2% decrease in the sample’s original mass, or a loss of

\[\mathrm{0.192\times146.11\;g/mol=28.1\;g/mol}\]

which is consistent with the loss of CO(g) and a residue of CaCO₃.

Finally, the loss of 5.30 mg from 600-800^oC is a 30.1% decrease in the sample’s original mass, or a loss of

\[\mathrm{0.301\times146.11\;g/mol=44.0\;g/mol}\]

This loss in molar mass is consistent with the release of CO₂(g), leaving a final residue of CaO.

Identifying the products of a thermal decomposition provides information that we can use to develop an analytical procedure. For example, the thermogram in Figure 8.10 shows that we must heat a precipitate of CaC₂O₄•H₂O to a temperature between 250 and 400^oC if we wish to isolate and weigh CaC₂O₄. Alternatively, heating the sample to 1000^oC allows us to isolate and weigh CaO.

Practice Exercise 8.6

Under the same conditions as Figure 8.10, the thermogram for a 22.16 mg sample of MgC₂O₄•H₂O shows two steps: a loss of 3.06 mg from 100–250^oC and a loss of 12.24 mg from 350–550^oC. For each step, identify the volatilization product and the solid residue that remains. Using your results from this exercise and the results from Example 8.4, explain how you can use thermogravimetry to analyze a mixture containing CaC₂O₄•H₂O and MgC₂O₄•H₂O. You may assume that other components in the sample are inert and thermally stable below 1000^oC.

Click here to review your answer to this exercise.

Equipment

Depending on the method of analysis, the equipment for volatilization gravimetry may be simple or complex. In the simplest experimental design, we place the sample in a crucible and decompose it at a fixed temperature using a Bunsen burner, a Meker burner, a laboratory oven, or a muffle furnace. The sample’s mass and the mass of the residue are measured using an analytical balance.

Trapping and weighing the volatile products of a thermal decomposition requires specialized equipment. The sample is placed in a closed container and heated. As decomposition occurs, a stream of an inert purge-gas sweeps the volatile products through one or more selective absorbent traps.

In a thermogravimetric analysis, the sample is placed on a small balance pan attached to one arm of an electromagnetic balance (Figure 8.11). The sample is lowered into an electric furnace and the furnace’s temperature is increased at a fixed rate of few degrees per minute while continuously monitoring the sample’s weight. The instrument usually includes a gas line for purging the volatile decomposition products out of the furnace, and a heat exchanger to dissipate the heat emitted by the furnace.

Figure 8.11 (a) Instrumentation for conducting a thermogravimetric analysis. The balance sits on the top of the instrument with the sample suspended below. A gas line supplies an inert gas that sweeps the volatile decomposition products out of the furnace. The heat exchanger dissipates the heat from the furnace to a reservoir of water. (b) Close-up showing the balance pan, which sits on a moving platform, the thermocouple for monitoring temperature, a hook for lowering the sample pan into the furnace, and the opening to the furnace. After placing a small portion of the sample on the balance pan, the platform rotates over the furnace and transfers the balance pan to a hook that is suspended from the balance. Once the balance pan is in place, the platform rotates back to its initial position. The balance pan and the thermocouple are then lowered into the furnace.

Note

The best way to appreciate the theoretical and practical details discussed in this section is to carefully examine a typical volatilization gravimetric method. Although each method is unique, the determination of Si in ores and alloys by forming volatile SiF₄ provides an instructive example of a typical procedure. The description here is based on a procedure from Young, R. S. Chemical Analysis in Extractive Metallurgy, Griffen: London, 1971, pp. 302–304.

Representative Method 8.2

Determination of Si in Ores and Alloys

Description of Method

Silicon is determined by dissolving the sample in acid and dehydrating to precipitate SiO₂. Because a variety of other insoluble oxides also form, the precipitate’s mass is not a direct measure of the amount of silicon in the sample. Treating the solid residue with HF results in the formation of volatile SiF₄. The decrease in mass following the loss of SiF₄ provides an indirect measure of the amount of silicon in the original sample.

Procedure

Transfer a sample of between 0.5 and 5.0 g to a platinum crucible along with an excess of Na₂CO₃, and heat until a melt forms. After cooling, dissolve the residue in dilute HCl. Evaporate the solution to dryness on a steam bath and heat the residue, which contains SiO₂ and other solids, for one hour at 110^oC. Moisten the residue with HCl and repeat the dehydration. Remove any acid soluble materials from the residue by adding 50 mL of water and 5 mL of concentrated HCl. Bring the solution to a boil and filter through #40 filter paper. (#40 filter paper is a medium speed, ashless filter paper for filtering crystalline solids.) Wash the residue with hot 2% v/v HCl followed by hot water. Evaporate the filtrate to dryness twice and, following the same procedure, treat to remove any acid-soluble materials. Combine the two precipitates, and dry and ignite to a constant weight at 1200^oC. After cooling, add 2 drops of 50% v/v H₂SO₄ and 10 mL of HF. Remove the volatile SiF₄ by evaporating to dryness on a hot plate. Finally, bring the residue to constant weight by igniting at 1200^oC.

Questions

1. According to the procedure the sample should weigh between 0.5 and 5.0 g. How should you decide upon the amount of sample to use?

In this procedure the critical measurement is the decrease in mass following the volatilization of SiF₄. The reaction responsible for the loss of mass is

\[\mathrm{SiO_2}(s)+\mathrm{4HF}(aq)\rightarrow\mathrm{SiF_4}(g)+\mathrm{2H_2O}(l)\]

Water and any excess HF are removed during the final ignition, and do not contribute to the change in mass. The loss in mass, therefore, is equivalent to the mass of SiO₂ present after the dehydration step. Every 0.1 g of Si in the original sample results in the loss of 0.21 g of SiO₂.

(Problem 8.31 asks you to verify that this loss of mass is correct.)

How much sample we use depends on what is an acceptable uncertainty when measuring mass. A 0.5-g sample that is 50% w/w in Si, for example, will lose 0.53 g. If we are using a balance that measures mass to the nearest ±0.1 mg, then the relative uncertainty in mass is approximately ±0.02%; this is a reasonable level of uncertainty for a gravimetric analysis. A 0.5 g sample that is only 5% w/w Si experiences a weight loss of only 0.053 g and has a relative uncertainty of ±0.2%. In this case a larger sample is needed.

2. Why are acid-soluble materials removed before treating the dehydrated residue with HF?

Any acid-soluble materials in the sample will react with HF or H₂SO₄. If the products of these reactions are volatile, or if they decompose at 1200^oC, then the change in mass is not due solely to the volatilization of SiF₄. As a result, we overestimate the amount of Si in our sample.

3. Why is H₂SO₄ added with the HF?

Many samples containing silicon also contain aluminum and iron, which, when dehydrating the sample, form Al₂O₃ and Fe₂O₃. These oxides are potential interferents because they also form volatile fluorides. In the presence of H₂SO₄, however, aluminum and iron preferentially form non-volatile sulfates. These sulfates eventually decompose back to their respective oxides when we heat the residue to 1200^oC. As a result, the change in weight after treating with HF and H₂SO₄ is due only to the loss of SiF₄.

8.3.2 Quantitative Applications

Unlike precipitation gravimetry, which is rarely used as a standard method of analysis, volatilization gravimetric methods continue to play an important role in chemical analysis. Several important examples are discussed below.

Inorganic Analysis

Determining the inorganic ash content of an organic material, such as a polymer, is an example of a direct volatilization gravimetric analysis. After weighing the sample, it is placed in an appropriate crucible and the organic material carefully removed by combustion, leaving behind the inorganic ash. The crucible containing the residue is heated to a constant weight using either a burner or an oven before determining the mass of the inorganic ash.

Another example of volatilization gravimetry is the determination of dissolved solids in natural waters and wastewaters. In this method, a sample of water is transferred to a weighing dish and dried to a constant weight at either 103–105^_oC or at 180^oC. Samples dried at the lower temperature retain some occluded water and lose some carbonate as CO₂. The loss of organic material, however, is minimal. At the higher temperature, the residue is free from occluded water, but the loss of carbonate is greater. In addition, some chloride, nitrate, and organic material is lost through thermal decomposition. In either case, the residue that remains after drying to a constant weight at 500^oC is the amount of fixed solids in the sample, and the loss in mass provides an indirect measure of the sample’s volatile solids.

Indirect analyses based on the weight of residue remaining after volatilization are commonly used in determining moisture in a variety of products, and in determining silica in waters, wastewaters, and rocks. Moisture is determined by drying a preweighed sample with an infrared lamp or a low temperature oven. The difference between the original weight and the weight after drying equals the mass of water lost.

Organic Analysis

The most important application of volatilization gravimetry is for the elemental analysis of organic materials. During combustion with pure O₂, many elements, such as carbon and hydrogen, are released as gaseous combustion products, such as CO₂(g) and H₂O(g). Passing the combustion products through preweighed tubes containing selective absorbents and measuring the increases in mass provides a direct analysis for the mass of carbon and hydrogen in the organic material.

Note

Instead of measuring mass, modern instruments for completing an elemental analysis use gas chromatography (Chapter 12) or infrared spectroscopy (Chapter 10) to monitor the gaseous decomposition products.

Alkaline metals and earths in organic materials can be determined by adding H₂SO₄ to the sample before combustion. After combustion is complete, the metal remains behind as a solid residue of metal sulfate. Silver, gold, and platinum can be determined by burning the organic sample, leaving a metallic residue of Ag, Au, or Pt. Other metals are determined by adding HNO₃ before combustion, leaving a residue of the metal oxide.

Volatilization gravimetry is also used to determine biomass in waters and wastewaters. Biomass is a water quality index that provides an indication of the total mass of organisms contained within a sample of water. A known volume of the sample is passed through a preweighed 0.45-μm membrane filter or a glass-fiber filter, and dried at 105^oC for 24 h. The residue’s mass provides a direct measure of biomass. If samples are known to contain a substantial amount of dissolved inorganic solids, the residue can be ignited at 500^oC for one hour, volatilizing the biomass. The resulting inorganic residue is wetted with distilled water to rehydrate any clay minerals and dried to a constant weight at 105^oC. The difference in mass before and after ignition provides an indirect measure of biomass.

Quantitative Calculations

For some applications, such as determining the amount of inorganic ash in a polymer, a quantitative calculation is straightforward and does not require a balanced chemical reaction. For other applications, however, the relationship between the analyte and the analytical signal depends upon the stoichiometry of any relevant reactions. Once again, a conservation of mass is useful when solving problems.

Example 8.5

A 101.3-mg sample of an organic compound containing chlorine is combusted in pure O₂ and the volatile gases collected in absorbent traps. The trap for CO₂ increases in mass by 167.6 mg and the trap for H₂O shows a 13.7-mg increase. A second sample of 121.8 mg is treated with concentrated HNO₃ producing Cl₂, which subsequently reacts with Ag⁺, forming 262.7 mg of AgCl. Determine the compound’s composition, as well as its empirical formula.

Solution

A conservation of mass requires that all the carbon in the organic compound must be in the CO₂ produced during combustion; thus

\[\mathrm{167.6\;mg\;CO_2\times\dfrac{1\;g\;CO_2}{1000\;mg\;CO_2}\times\dfrac{1\;mol\;C}{44.011\;g\;CO_2}\times\dfrac{12.011\;g\;C}{mol\;C}\times\dfrac{1000\;mg\;C}{g\;C}=45.74\;mg\;C}\]

\[\mathrm{\dfrac{45.74\;mg\;C}{101.3\;mg\;sample}\times100=45.15\%\;w/w\;C}\]

Using the same approach for hydrogen and chlorine, we find that

\[\mathrm{13.7\;mg\;H_2O\times\dfrac{1\;g\;H_2O}{1000\;mg\;H_2O}\times\dfrac{2\;mol\;H}{18.015\;g\;H_2O}\times\dfrac{1.008\;g\;H}{mol\;H}\times\dfrac{1000\;mg\;H}{g\;H}=1.533\;mg\;H}\]

\[\mathrm{\dfrac{1.533\;mg\;H}{101.3\;mg\;sample}\times100=1.51\%\;w/w\;H}\]

\[\mathrm{262.7\;mg\;AgCl\times\dfrac{1\;g\;AgCl}{1000\;mg\;AgCl}\times\dfrac{1\;mol\;Cl}{143.32\;g\;AgCl}\times\dfrac{35.453\;g\;Cl}{mol\;Cl}\times\dfrac{1000\;mg\;Cl}{g\;Cl}=64.98\;mg\;Cl}\]

\[\mathrm{\dfrac{64.98\;mg\;Cl}{121.8\;mg\;sample}\times100=53.35\%\;w/w\;Cl}\]

Adding together the weight percents for C, H, and Cl gives a total of 100.01%; thus, the compound contains only these three elements. To determine the compound’s empirical formula we note that a gram of sample contains 0.4515 g of C, 0.0151 g of H and 0.5335 g of Cl. Expressing each element in moles gives 0.0376 moles C, 0.0150 moles H and 0.0150 moles Cl. Hydrogen and chlorine are present in a 1:1 molar ratio. The molar ratio of C to moles of H or Cl is

\[\mathrm{\dfrac{moles\;C}{moles\;H}=\dfrac{moles\;C}{moles\;Cl}=\dfrac{0.0376}{0.0150}=2.51\approx2.5}\]

Thus, the simplest, or empirical formula for the compound is C₅H₂Cl₂.

In an indirect volatilization gravimetric analysis, the change in the sample’s weight is proportional to the amount of analyte. Note that in the following example it is not necessary to apply a conservation of mass to relate the analytical signal to the analyte.

Example 8.6

A sample of slag from a blast furnace is analyzed for SiO₂ by decomposing a 0.5003-g sample with HCl, leaving a residue with a mass of 0.1414 g. After treating with HF and H₂SO₄, and evaporating the volatile SiF₄, a residue with a mass of 0.0183 g remains. Determine the %w/w SiO₂ in the sample.

Solution

In this procedure the difference in the residue’s mass before and after volatilizing SiF₄ gives the mass of SiO₂ in the sample; thus the sample contains

\[\mathrm{0.1414\,g-0.0183\,g=0.1231\,g\,SiO_2}\]

and the %w/w SiO₂ is

\[\mathrm{\dfrac{0.1231\;g\;SiO_2}{0.5003\;g}\times100=24.61\%\;w/w\;SiO_2}\]

Practice Exercise 8.7

Heating a 0.3317-g mixture of CaC₂O₄ and MgC₂O₄ yields a residue of 0.1794 g at 600^oC and a residue of 0.1294 g at 1000^oC. Calculate the %w/w CaC₂O₄ in the sample. You may wish to review your answer to Practice Exercise 8.6 as you consider this problem.

Click here to review your answer to this exercise.

Finally, in some quantitative applications we can compare the result for a sample to a similar result obtained using a standard.

Example 8.7

A 26.23-mg sample of MgC₂O₄•H₂O and inert materials is heated to constant weight at 1200^oC, leaving a residue weighing 20.98 mg. A sample of pure MgC₂O₄•H₂O, when treated in the same fashion, undergoes a 69.08% change in its mass. Determine the %w/w MgC₂O₄•H₂O in the sample.

Solution

The change in the sample’s mass is 5.25 mg, which corresponds to

\[\mathrm{5.25\;mg\;lost\times\dfrac{100.0\;mg\;MgC_2O_4\cdot H_2O}{69.08\;mg\;lost}=7.60\;mg\;MgC_2O_4\cdot H_2O}\]

The %w/w MgC₂O₄•H₂O in the sample is

\[\mathrm{\dfrac{7.60\;mg\;MgC_2O_4\cdot H_2O}{26.23\;mg\;sample}\times 100=29.0\%\;w/w\;MgC_2O_4\cdot H_2O}\]

(Alternatively, you can determine that the final product of the decomposition is MgO (see Practice Exercise 8.6) and use a conservation of mass for Mg to arrive at the same answer.)

8.3.3 Evaluating Volatilization Gravimetry

The scale of operation, accuracy, and precision of a gravimetric volatilization method is similar to that described in Section 8B.4 for precipitation gravimetry. The sensitivity of a direct analysis is fixed by the analyte’s chemical form following combustion or volatilization. We can improve the sensitivity of an indirect analysis by choosing conditions that give the largest possible change in mass. For example, the thermogram in Figure 8.10 shows us that an indirect analysis for CaC₂O₄•H₂O is more sensitive if we measure the change in mass following ignition at 1000^oC than if we ignite the sample at 300^oC.

Selectivity is not a problem for a direct analysis if we trap the analyte using a selective absorbent trap. A direct analysis based on the residue’s weight following combustion or volatilization is possible if the residue only contains the analyte of interest. As noted earlier, an indirect analysis is only feasible when the change in mass results from the loss of a single volatile product containing the analyte.

Volatilization gravimetric methods are time and labor intensive. Equipment needs are few, except when combustion gases must be trapped, or for a thermogravimetric analysis, when specialized instrumentation is needed.

Contributors

David Harvey (DePauw University)