3.5: Cell Potential Under Nonstandard Conditions

Learning Objectives

• Relate cell potentials to Gibbs energy changes
• Use the Nernst equation to determine cell potentials at nonstandard conditions
• Perform calculations that involve converting between cell potentials, free energy changes, and equilibrium constants

The Nernst Equation enables the determination of cell potential under non-standard conditions. It relates the measured cell potential to the reaction quotient and allows the accurate determination of equilibrium constants (including solubility constants).

The Effect of Concentration on Cell Potential: The Nernst Equation

Recall that the actual free-energy change for a reaction under nonstandard conditions, \(\Delta{G}\), is given as follows:

\[\Delta{G} = \Delta{G°} + RT \ln Q \label{Eq1}\]

We also know that ΔG = −nFE_cell and ΔG° = −nFE°_cell. Substituting these expressions into Equation \(\ref{Eq1}\), we obtain

\[−nFE_{cell} = −nFE^o_{cell} + RT \ln Q \label{Eq2}\]

Dividing both sides of this equation by \(−nF\),

\[E_\textrm{cell}=E^\circ_\textrm{cell}-\left(\dfrac{RT}{nF}\right)\ln Q \label{Eq3}\]

Equation \(\ref{Eq3}\) is called the Nernst equation, after the German physicist and chemist Walter Nernst (1864–1941), who first derived it. The Nernst equation is arguably the most important relationship in electrochemistry. When a redox reaction is at equilibrium (\(ΔG = 0\)), then Equation \(\ref{Eq3}\) reduces to Equation \(\ref{Eq31}\) and \(\ref{Eq32}\) because \(Q = K\), and there is no net transfer of electrons (i.e., E_cell = 0).

\[E_\textrm{cell}=E^\circ_\textrm{cell}-\left(\dfrac{RT}{nF}\right)\ln K = 0 \label{Eq31}\]

since

\[E^\circ_\textrm{cell}= \left(\dfrac{RT}{nF}\right)\ln K \label{Eq32}\]

Substituting the values of the constants into Equation \(\ref{Eq3}\) with T = 298 K and converting to base-10 logarithms give the relationship of the actual cell potential (E_cell), the standard cell potential (E°_cell), and the reactant and product concentrations at room temperature (contained in \(Q\)):

\[E_{\textrm{cell}}=E^\circ_\textrm{cell}-\left(\dfrac{\textrm{0.0591 V}}{n}\right)\log Q \label{Eq4}\]

The Power of the Nernst Equation

The Nernst Equation (\(\ref{Eq3}\)) can be used to determine the value of E_cell, and thus the direction of spontaneous reaction, for any redox reaction under any conditions.

Equation \(\ref{Eq4}\) allows us to calculate the potential associated with any electrochemical cell at 298 K for any combination of reactant and product concentrations under any conditions. We can therefore determine the spontaneous direction of any redox reaction under any conditions, as long as we have tabulated values for the relevant standard electrode potentials. Notice in Equation \(\ref{Eq4}\) that the cell potential changes by 0.0591/n V for each 10-fold change in the value of Q because log 10 = 1.

Example \(\PageIndex{1}\)

The following reaction proceeds spontaneously under standard conditions because E°_cell > 0 (which means that ΔG° < 0):

2Ce⁴⁺(aq) + 2Cl^–(aq) → 2Ce³⁺(aq) + Cl₂(g) E°_cell = 0.25 V

Calculate \(E_{cell}\) for this reaction under the following nonstandard conditions and determine whether it will occur spontaneously: [Ce⁴⁺] = 0.013 M, [Ce³⁺] = 0.60 M, [Cl⁻] = 0.0030 M, \(P_\mathrm{Cl_2}\) = 1.0 atm, and T = 25°C.

Given: balanced redox reaction, standard cell potential, and nonstandard conditions

Asked for: cell potential

Strategy:

Determine the number of electrons transferred during the redox process. Then use the Nernst equation to find the cell potential under the nonstandard conditions.

SOLUTION

We can use the information given and the Nernst equation to calculate E_cell. Moreover, because the temperature is 25°C (298 K), we can use Equation \(\ref{Eq4}\) instead of Equation \(\ref{Eq3}\). The overall reaction involves the net transfer of two electrons:

\[2Ce^{4+}_{(aq)} + 2e^− \rightarrow 2Ce^{3+}_{(aq)} onumber \]

\[2Cl^−_{(aq)} \rightarrow Cl_{2(g)} + 2e^− onumber \]

so n = 2. Substituting the concentrations given in the problem, the partial pressure of Cl₂, and the value of E°_cell into Equation \(\ref{Eq4}\),

\[\begin{align*}E_\textrm{cell} & =E^\circ_\textrm{cell}-\left(\dfrac{\textrm{0.0591 V}}{n}\right)\log Q \\
& =\textrm{0.25 V}-\left(\dfrac{\textrm{0.0591 V}}{2}\right)\log\left(\dfrac{[\mathrm{Ce^{3+}}]^2P_\mathrm{Cl_2}}{[\mathrm{Ce^{4+}}]^2[\mathrm{Cl^-}]^2}\right) \\
& =\textrm{0.25 V}-[(\textrm{0.0296 V})(8.37)]=\textrm{0.00 V}\end{align*}\]

Thus the reaction will not occur spontaneously under these conditions (because E = 0 V and ΔG = 0). The composition specified is that of an equilibrium mixture

Exercise \(\PageIndex{1}\)

Molecular oxygen will not oxidize \(MnO_2\) to permanganate via the reaction

\[4MnO_{2(s)} + 3O_{2(g)} + 4OH^−_{(aq)} \rightarrow 4MnO^−_{4(aq)} + 2H_2O_{(l)} \;\;\; E°_{cell} = −0.20\; V onumber \]

Calculate \(E_{cell}\) for the reaction under the following nonstandard conditions and decide whether the reaction will occur spontaneously: pH 10, \(P_\mathrm{O_2}\)= 0.20 atm, [MNO₄⁻] = 1.0 × 10⁻⁴ M, and T = 25°C.

Answer

E_cell = −0.22 V; the reaction will not occur spontaneously.

Applying the Nernst equation to a simple electrochemical cell such as the Zn/Cu cell allows us to see how the cell voltage varies as the reaction progresses and the concentrations of the dissolved ions change. Recall that the overall reaction for this cell is as follows:

\[Zn(s) + Cu^{2+}(aq) \rightarrow Zn^{2+}(aq) + Cu(s)\;\;\;E°cell = 1.10 V \label{Eq5}\]

The reaction quotient is therefore \(Q = [Zn^{2+}]/[Cu^{2+}]\). Suppose that the cell initially contains 1.0 M Cu²⁺ and 1.0 × 10⁻⁶ M Zn²⁺. The initial voltage measured when the cell is connected can then be calculated from Equation \(\ref{Eq4}\):

\[\begin{align}E_\textrm{cell} & =E^\circ_\textrm{cell}-\left(\dfrac{\textrm{0.0591 V}}{n}\right)\log\dfrac{[\mathrm{Zn^{2+}}]}{[\mathrm{Cu^{2+}}]}\\
& =\textrm{1.10 V}-\left(\dfrac{\textrm{0.0591 V}}{2}\right)\log\left(\dfrac{1.0\times10^{-6}}{1.0}\right)=\textrm{1.28 V}\end{align} \label{Eq6}\]

Thus the initial voltage is greater than E° because \(Q<1\). As the reaction proceeds, [Zn²⁺] in the anode compartment increases as the zinc electrode dissolves, while [Cu²⁺] in the cathode compartment decreases as metallic copper is deposited on the electrode. During this process, the ratio Q = [Zn²⁺]/[Cu²⁺] steadily increases, and the cell voltage therefore steadily decreases. Eventually, [Zn²⁺] = [Cu²⁺], so Q = 1 and E_cell = E°_cell. Beyond this point, [Zn²⁺] will continue to increase in the anode compartment, and [Cu²⁺] will continue to decrease in the cathode compartment. Thus the value of Q will increase further, leading to a further decrease in E_cell. When the concentrations in the two compartments are the opposite of the initial concentrations (i.e., 1.0 M Zn²⁺ and 1.0 × 10⁻⁶ M Cu²⁺), Q = 1.0 × 10⁶, and the cell potential will be reduced to 0.92 V.

Figure \(\PageIndex{1}\): The Variation of E_cell with Log Q for a Zn/Cu Cell. Initially, log Q < 0, and the voltage of the cell is greater than E°_cell. As the reaction progresses, log Q increases, and E_cell decreases. When [Zn²⁺] = [Cu²⁺], log Q = 0 and E_cell = E°_cell = 1.10 V. As long as the electrical circuit remains intact, the reaction will continue, and log Q will increase until Q = K and the cell voltage reaches zero. At this point, the system will have reached equilibrium.

The variation of E_cell with \(\log{Q}\) over this range is linear with a slope of −0.0591/n, as illustrated in Figure \(\PageIndex{1}\). As the reaction proceeds still further, \(Q\) continues to increase, and E_cell continues to decrease. If neither of the electrodes dissolves completely, thereby breaking the electrical circuit, the cell voltage will eventually reach zero. This is the situation that occurs when a battery is “dead.” The value of \(Q\) when E_cell = 0 is calculated as follows:

\[\begin{align}E_\textrm{cell} &=E^\circ_\textrm{cell}-\left(\dfrac{\textrm{0.0591 V}}{n}\right)\log Q=0 \\
E^\circ &=\left(\dfrac{\textrm{0.0591 V}}{n}\right)\log Q \\
\log Q &=\dfrac{E^\circ n}{\textrm{0.0591 V}}=\dfrac{(\textrm{1.10 V})(2)}{\textrm{0.0591 V}}=37.23 \\
Q &=10^{37.23}=1.7\times10^{37}\end{align} \label{Eq7}\]

Recall that at equilibrium, \(Q = K\). Thus the equilibrium constant for the reaction of Zn metal with Cu²⁺ to give Cu metal and Zn²⁺ is 1.7 × 10³⁷ at 25°C.

Concentration Cells

A voltage can also be generated by constructing an electrochemical cell in which each compartment contains the same redox active solution but at different concentrations. The voltage is produced as the concentrations equilibrate. Suppose, for example, we have a cell with 0.010 M AgNO₃ in one compartment and 1.0 M AgNO₃ in the other. The cell diagram and corresponding half-reactions are as follows:

\[Ag(s)\,|\,Ag^+(aq, 0.010 \;M)\,||\,Ag+(aq, 1.0 \;M)\,|\,Ag(s) \label{Eq8}\]

cathode:

\[Ag^+(aq, 1.0\; M) + e^− \rightarrow Ag(s) \label{Eq9}\]

anode:

\[Ag(s) \rightarrow Ag^+(aq, 0.010\; M) + e^− \label{Eq10}\]

Overall

\[Ag^+(aq, 1.0 \;M) \rightarrow Ag^+(aq, 0.010\; M) \label{Eq11}\]

As the reaction progresses, the concentration of \(Ag^+\) will increase in the left (oxidation) compartment as the silver electrode dissolves, while the \(Ag^+\) concentration in the right (reduction) compartment decreases as the electrode in that compartment gains mass. The total mass of \(Ag(s)\) in the cell will remain constant, however. We can calculate the potential of the cell using the Nernst equation, inserting 0 for E°_cell because E°_cathode = −E°_anode:

\[\begin{align} E_\textrm{cell}&=E^\circ_\textrm{cell}-\left(\dfrac{\textrm{0.0591 V}}{n}\right)\log Q \\[4pt] &=0-\left(\dfrac{\textrm{0.0591 V}}{1}\right)\log\left(\dfrac{0.010}{1.0}\right) \\[4pt] &=\textrm{0.12 V} \end{align}\]

An electrochemical cell of this type, in which the anode and cathode compartments are identical except for the concentration of a reactant, is called a concentration cell. As the reaction proceeds, the difference between the concentrations of Ag⁺ in the two compartments will decrease, as will E_cell. Finally, when the concentration of Ag⁺ is the same in both compartments, equilibrium will have been reached, and the measured potential difference between the two compartments will be zero (E_cell = 0).

Example \(\PageIndex{2}\)

Calculate the voltage in a galvanic cell that contains a manganese electrode immersed in a 2.0 M solution of MnCl₂ as the cathode, and a manganese electrode immersed in a 5.2 × 10⁻² M solution of MnSO₄ as the anode (T = 25°C).

Given: galvanic cell, identities of the electrodes, and solution concentrations

Asked for: voltage

Strategy:

1. Write the overall reaction that occurs in the cell.
2. Determine the number of electrons transferred. Substitute this value into the Nernst equation to calculate the voltage.

Solution:

A This is a concentration cell, in which the electrode compartments contain the same redox active substance but at different concentrations. The anions (Cl⁻ and SO₄²⁻) do not participate in the reaction, so their identity is not important. The overall reaction is as follows:

\[Mn^{2+}_{(aq, 2.0 M)} \rightarrow Mn^{2+}_{(aq, 5.2 \times 10^{−2} M)} onumber \]

B For the reduction of Mn²⁺(aq) to Mn(s), n = 2. We substitute this value and the given Mn²⁺ concentrations into Equation \(\ref{Eq4}\):

\[E_\textrm{cell}=E^\circ_\textrm{cell}-\left(\dfrac{\textrm{0.0591 V}}{n}\right)\log Q=\textrm{0 V}-\left(\dfrac{\textrm{0.0591 V}}{2}\right)\log\left(\dfrac{5.2\times10^{-2}}{2.0}\right)=\textrm{0.047 V} onumber \]

Thus manganese will dissolve from the electrode in the compartment that contains the more dilute solution and will be deposited on the electrode in the compartment that contains the more concentrated solution.

Exercise \(\PageIndex{2}\)

Suppose we construct a galvanic cell by placing two identical platinum electrodes in two beakers that are connected by a salt bridge. One beaker contains 1.0 M HCl, and the other a 0.010 M solution of Na₂SO₄ at pH 7.00. Both cells are in contact with the atmosphere, with \(P_\mathrm{O_2}\) = 0.20 atm. If the relevant electrochemical reaction in both compartments is the four-electron reduction of oxygen to water:

\[O_{2(g)} + 4H^+_{(aq)} + 4e^− \rightarrow 2H_2O_{(l)} onumber \]

What will be the potential when the circuit is closed?

Answer

0.41 V

Using Cell Potentials to Measure Solubility Products

Because voltages are relatively easy to measure accurately using a voltmeter, electrochemical methods provide a convenient way to determine the concentrations of very dilute solutions and the solubility products (K_sp) of sparingly soluble substances. As you learned previously, solubility products can be very small, with values of less than or equal to 10⁻³⁰. Equilibrium constants of this magnitude are virtually impossible to measure accurately by direct methods, so we must use alternative methods that are more sensitive, such as electrochemical methods.

To understand how an electrochemical cell is used to measure a solubility product, consider the cell shown in Figure \(\PageIndex{1}\), which is designed to measure the solubility product of silver chloride: K_sp = [Ag⁺][Cl⁻]. In one compartment, the cell contains a silver wire inserted into a 1.0 M solution of Ag⁺; the other compartment contains a silver wire inserted into a 1.0 M Cl⁻ solution saturated with AgCl. In this system, the Ag⁺ ion concentration in the first compartment equals K_sp. We can see this by dividing both sides of the equation for K_sp by [Cl⁻] and substituting: [Ag⁺] = K_sp/[Cl⁻] = K_sp/1.0 = K_sp. The overall cell reaction is as follows:

Ag⁺(aq, concentrated) → Ag⁺(aq, dilute)

Thus the voltage of the concentration cell due to the difference in [Ag⁺] between the two cells is as follows:

\[E_\textrm{cell}=\textrm{0 V}-\left(\dfrac{\textrm{0.0591 V}}{1}\right)\log\left(\dfrac{[\mathrm{Ag^+}]_\textrm{dilute}}{[\mathrm{Ag^+}]_\textrm{concentrated}}\right)= \label{Eq121}\]

\[-\textrm{0.0591 V } \log\left(\dfrac{K_{\textrm{sp}}}{1.0}\right)=-\textrm{0.0591 V }\log K_{\textrm{sp}} \label{Eq122}\]

Figure \(\PageIndex{1}\): A Galvanic ("Concentration") Cell for Measuring the Solubility Product of AgCl. One compartment contains a silver wire inserted into a 1.0 M solution of Ag⁺, and the other compartment contains a silver wire inserted into a 1.0 M Cl⁻ solution saturated with AgCl. The potential due to the difference in [Ag⁺] between the two cells can be used to determine K_sp.

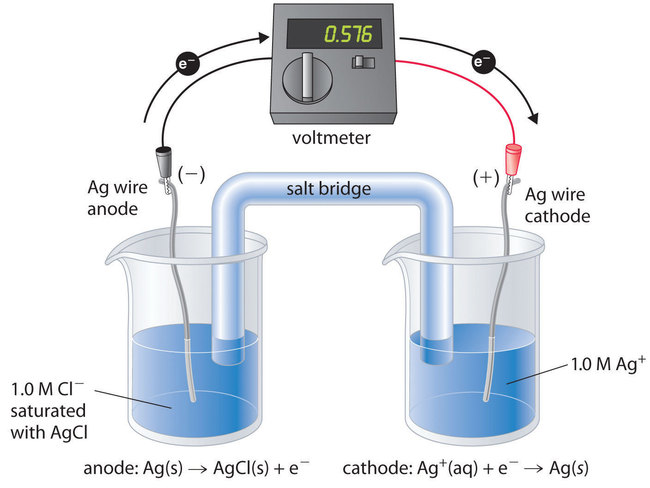
By closing the circuit, we can measure the potential caused by the difference in [Ag+] in the two cells. In this case, the experimentally measured voltage of the concentration cell at 25°C is 0.580 V. Solving Equation \(\ref{Eq1}\)2 for Ksp,

\[\begin{align}\log K_\textrm{sp} & =\dfrac{-E_\textrm{cell}}{\textrm{0.0591 V}}=\dfrac{-\textrm{0.580 V}}{\textrm{0.0591 V}}=-9.81 \\
K_\textrm{sp} & =1.5\times10^{-10}\end{align} \label{Eq13}\]

Thus a single potential measurement can provide the information we need to determine the value of the solubility product of a sparingly soluble salt.+

Example \(\PageIndex{3}\)

To measure the solubility product of lead(II) sulfate (PbSO₄) at 25°C, you construct a galvanic cell like the one shown in Figure \(\PageIndex{1}\), which contains a 1.0 M solution of a very soluble Pb²⁺ salt [lead(II) acetate trihydrate] in one compartment that is connected by a salt bridge to a 1.0 M solution of Na₂SO₄ saturated with PbSO₄ in the other. You then insert a Pb electrode into each compartment and close the circuit. Your voltmeter shows a voltage of 230 mV. What is K_sp for PbSO₄? Report your answer to two significant figures.

Given: galvanic cell, solution concentrations, electrodes, and voltage

Asked for: K_sp

Strategy:

1. From the information given, write the equation for K_sp. Express this equation in terms of the concentration of Pb²⁺.
2. Determine the number of electrons transferred in the electrochemical reaction. Substitute the appropriate values into Equation \(\ref{Eq1}\)2 and solve for K_sp.

Solution:

A You have constructed a concentration cell, with one compartment containing a 1.0 M solution of Pb2+ and the other containing a dilute solution of Pb²⁺ in 1.0 M Na₂SO₄. As for any concentration cell, the voltage between the two compartments can be calculated using the Nernst equation. The first step is to relate the concentration of Pb²⁺ in the dilute solution to K_sp:

\[\begin{align*}[\mathrm{Pb^{2+}}][\mathrm{SO_4^{2-}}] & =K_\textrm{sp} \\
[\mathrm{Pb^{2+}}] &=\dfrac{K_\textrm{sp}}{[\mathrm{SO_4^{2-}}]}=\dfrac{K_\textrm{sp}}{\textrm{1.0 M}}=K_\textrm{sp}\end{align*}\]

B The reduction of Pb²⁺ to Pb is a two-electron process and proceeds according to the following reaction:

Pb²⁺(aq, concentrated) → Pb²⁺(aq, dilute)

so

\[\begin{align*}E_\textrm{cell} &=E^\circ_\textrm{cell}-\left(\dfrac{0.0591}{n}\right)\log Q \\
\textrm{0.230 V} & =\textrm{0 V}-\left(\dfrac{\textrm{0.0591 V}}{2}\right)\log\left(\dfrac{[\mathrm{Pb^{2+}}]_\textrm{dilute}}{[\mathrm{Pb^{2+}}]_\textrm{concentrated}}\right)=-\textrm{0.0296 V}\log\left(\dfrac{K_\textrm{sp}}{1.0}\right) \\
-7.77 & =\log K_\textrm{sp} \\
1.7\times10^{-8} & =K_\textrm{sp}\end{align*}\]

Exercise \(\PageIndex{3}\)

A concentration cell similar to the one described in Example \(\PageIndex{3}\) contains a 1.0 M solution of lanthanum nitrate [La(NO₃)₃] in one compartment and a 1.0 M solution of sodium fluoride saturated with LaF₃ in the other. A metallic La strip is inserted into each compartment, and the circuit is closed. The measured potential is 0.32 V. What is the K_sp for LaF₃? Report your answer to two significant figures.

Answer

5.7 × 10⁻¹⁷

Using Cell Potentials to Measure Concentrations

Another use for the Nernst equation is to calculate the concentration of a species given a measured potential and the concentrations of all the other species. We saw an example of this in Example \(\PageIndex{3}\), in which the experimental conditions were defined in such a way that the concentration of the metal ion was equal to K_sp. Potential measurements can be used to obtain the concentrations of dissolved species under other conditions as well, which explains the widespread use of electrochemical cells in many analytical devices. Perhaps the most common application is in the determination of [H⁺] using a pH meter, as illustrated in Example 20.5.6.

Example \(\PageIndex{4}\): Measuring pH

Suppose a galvanic cell is constructed with a standard Zn/Zn²⁺ couple in one compartment and a modified hydrogen electrode in the second compartment. The pressure of hydrogen gas is 1.0 atm, but [H⁺] in the second compartment is unknown. The cell diagram is as follows:

Zn(s)∣Zn²⁺(aq, 1.0 M) ∥ H⁺(aq, ? M)∣H₂(g, 1.0 atm)∣Pt(s)

What is the pH of the solution in the second compartment if the measured potential in the cell is 0.26 V at 25°C?

Given: galvanic cell, cell diagram, and cell potential

Asked for: pH of the solution

Strategy:

1. Write the overall cell reaction.
2. Substitute appropriate values into the Nernst equation and solve for −log[H⁺] to obtain the pH.

Solution:

A Under standard conditions, the overall reaction that occurs is the reduction of protons by zinc to give H₂ (note that Zn lies below H₂ in Table P2):

Zn(s) + 2H²⁺(aq) → Zn²⁺(aq) + H₂(g) E°=0.76 V

B By substituting the given values into the simplified Nernst equation (Equation \(\ref{Eq4}\)), we can calculate [H⁺] under nonstandard conditions:

\[\begin{align}E_\textrm{cell} &=E^\circ_\textrm{cell}-\left(\dfrac{\textrm{0.0591 V}}n\right)\log\left(\dfrac{[\mathrm{Zn^{2+}}]P_\mathrm{H_2}}{[\mathrm{H^+}]^2}\right) \\
\textrm{0.26 V} &=\textrm{0.76 V}-\left(\dfrac{\textrm{0.0591 V}}2\right)\log\left(\dfrac{(1.0)(1.0)}{[\mathrm{H^+}]^2}\right) \\
16.9 &=\log\left(\dfrac{1}{[\mathrm{H^+}]^2}\right)=\log[\mathrm{H^+}]^{-2}=(-2)\log[\mathrm{H^+}] \\
8.46 &=-\log[\mathrm{H^+}] \\
8.5 &=\mathrm{pH}\end{align}\]

Thus the potential of a galvanic cell can be used to measure the pH of a solution.

Exercise \(\PageIndex{4}\)

Suppose you work for an environmental laboratory and you want to use an electrochemical method to measure the concentration of Pb²⁺ in groundwater. You construct a galvanic cell using a standard oxygen electrode in one compartment (E°_cathode = 1.23 V). The other compartment contains a strip of lead in a sample of groundwater to which you have added sufficient acetic acid, a weak organic acid, to ensure electrical conductivity. The cell diagram is as follows:

\[Pb_{(s)} ∣Pb^{2+}(aq, ? M)∥H^+(aq), 1.0 M∣O_2(g, 1.0 atm)∣Pt_{(s)} onumber \]

When the circuit is closed, the cell has a measured potential of 1.62 V. Use Table P2 to determine the concentration of Pb²⁺ in the groundwater.

Answer

\(1.2 \times 10^{−9}\; M\)

Summary

The Nernst equation can be used to determine the direction of spontaneous reaction for any redox reaction in aqueous solution. The Nernst equation allows us to determine the spontaneous direction of any redox reaction under any reaction conditions from values of the relevant standard electrode potentials. Concentration cells consist of anode and cathode compartments that are identical except for the concentrations of the reactant. Because ΔG = 0 at equilibrium, the measured potential of a concentration cell is zero at equilibrium (the concentrations are equal). A galvanic cell can also be used to measure the solubility product of a sparingly soluble substance and calculate the concentration of a species given a measured potential and the concentrations of all the other species.