4.7: Multiple Bonds in VB Theory

Learning Objectives

• To explain multiple bonds in terms of hybridized and unhybridized atomic orbitals according to Valence Bond Theory.

So far in our bonding descriptions according to Valence Bond Theory, we have not dealt with polyatomic systems with multiple bonds. To do so, we can use an approach in which we describe \(\sigma\) bonding using localized electron-pair bonds formed by hybrid atomic orbitals, and \(\pi\) bonding using unhybridized np atomic orbitals.

Non-singular Bonding

We begin our discussion by considering the bonding in ethylene (C₂H₄). Experimentally, we know that the H–C–H and H–C–C angles in ethylene are approximately 120°. This angle suggests that the carbon atoms are sp² hybridized, which means that a singly occupied sp² orbital on one carbon overlaps with a singly occupied s orbital on each H and a singly occupied sp² lobe on the other C. Thus each carbon forms a set of three \(\sigma\) bonds: two C–H (sp² + s) and one C–C (sp² + sp²) (part (a) in Figure 4.7.1). The sp² hybridization can be represented as follows:

Figure 4.7.1 Bonding in Ethylene. (a) The \(\sigma\)-bonded framework is formed by the overlap of two sets of singly occupied carbon sp² hybrid orbitals and four singly occupied hydrogen 1s orbitals to form electron-pair bonds. This uses 10 of the 12 valence electrons to form a total of five \(\sigma\) bonds (four C–H bonds and one C–C bond). (b) One singly occupied unhybridized 2p_z orbital remains on each carbon atom to form a carbon–carbon \(\pi\) bond. (Note: by convention, in planar molecules the axis perpendicular to the molecular plane is the z-axis.)

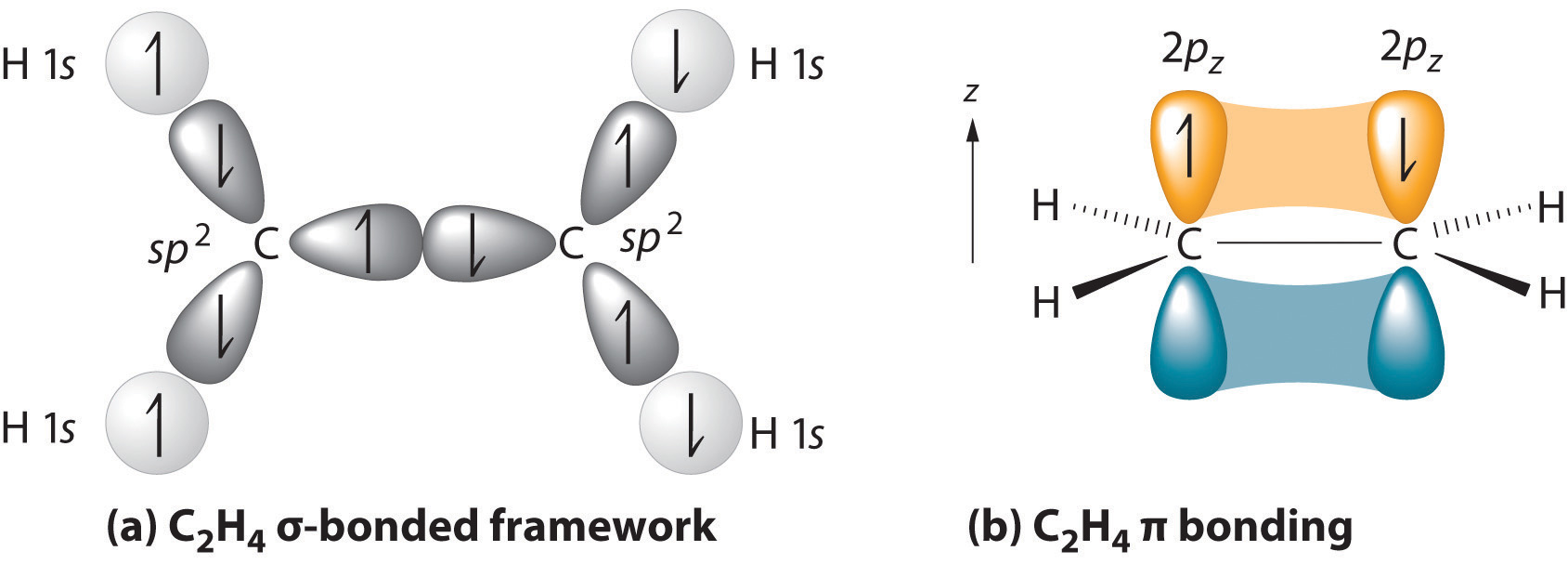
After hybridization, each carbon still has one unhybridized 2p_z orbital that is perpendicular to the hybridized lobes and contains a single electron (part (b) in Figure 4.7.1). The two singly occupied 2p_z orbitals can overlap to form a \(\pi\) bond. This is only possible when the two orbitals are arranged parallel. Rather than electron density along the internuclear axis, the \(\pi\) bond has a nodal plane along the internuclear axis with the electron density above and below the axis. Because each 2p_z orbital has a single electron, there are two electrons in the \(\pi\) bond. Consequently, the C–C bond in ethylene consists of a \(\sigma\) bond and a \(\pi\) bond, which together give a C=C double bond. Thus, the bond order between the two carbon atoms is 2.

Our model is supported by the facts that the measured carbon–carbon bond is shorter than that in ethane (133.9 pm versus 153.5 pm) and the bond is stronger (728 kJ/mol versus 376 kJ/mol in ethane). The two CH₂ fragments are coplanar, which maximizes the overlap of the two singly occupied 2p_z orbitals.

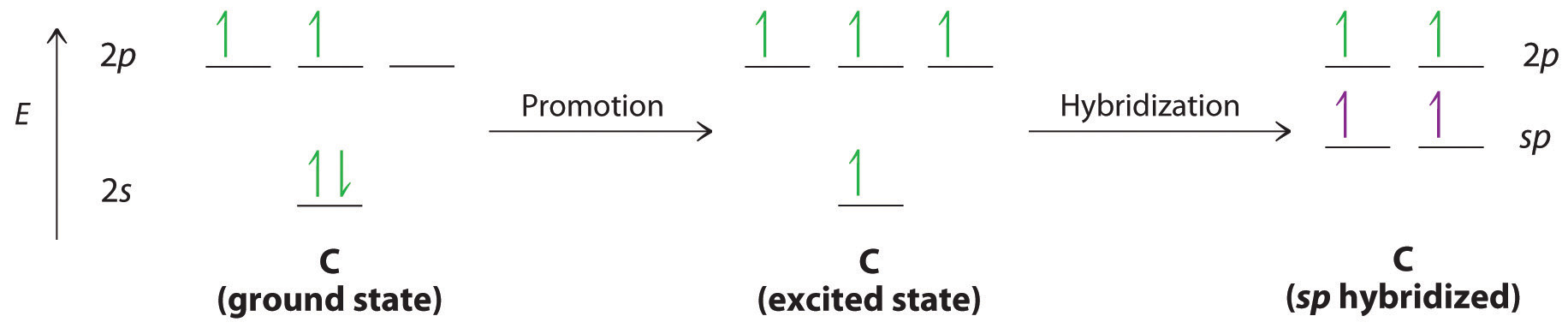
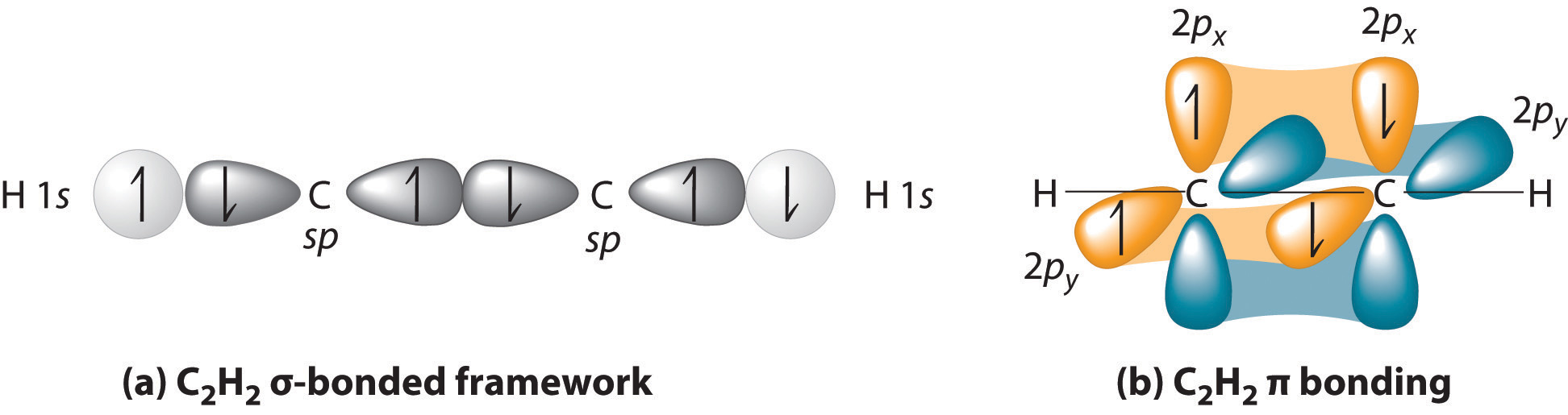
Now, consider triple bonds, as in acetylene (C₂H₂). Here the four atoms of acetylene are collinear, which suggests that each carbon is sp hybridized. If one sp lobe on each carbon atom is used to form a C–C \(\sigma\) bond and one is used to form the C–H \(\sigma\) bond, then each carbon will still have two unhybridized 2p orbitals (a 2p_x,y pair), each with one electron (part (a) in Figure 4.7.3).

Figure 4.7.3). Because each of the unhybridized 2p orbitals has a single electron, four electrons are available for \(\pi\) bonding, two in each \(\pi\) bond. Acetylene must therefore have a carbon–carbon triple bond, which consists of a C–C \(\sigma\) bond and two mutually perpendicular \(\pi\) bonds. Acetylene does in fact have a shorter carbon–carbon bond (120.3 pm) and a higher bond energy (965 kJ/mol) than ethane and ethylene, as we would expect for a triple bond.

Figure 4.7.3 Bonding in Acetylene (a) In the formation of the \(\sigma\)-bonded framework, two sets of singly occupied carbon sp hybrid orbitals and two singly occupied hydrogen 1s orbitals overlap. (b) In the formation of two carbon–carbon \(\pi\) bonds in acetylene, two singly occupied unhybridized 2p_x,y orbitals on each carbon atom overlap. With one \(\sigma\) bond plus two \(\pi\) bonds, the carbon–carbon bond order in acetylene is 3.

Note

In complex molecules, hybrid orbitals and valence bond theory can be used to describe \(\sigma\) bonding, and unhybridized \(\pi\) orbitals can be used to describe \(\pi\) bonding.

Example 4.7.1

Describe the bonding in HCN using a combination of hybrid atomic orbitals and unhybridized atomic orbitals. The HCN molecule is linear.

Given: chemical compound and molecular geometry

Asked for: bonding description using hybrid atomic orbitals and unhybridized orbitals

Strategy:

1. From the geometry given, predict the hybridization in HCN. Use the hybrid orbitals to form the \(\sigma\)-bonded framework of the molecule and determine the number of valence electrons that are used for \(\sigma\) bonding.
2. Determine the number of remaining valence electrons. Use any remaining unhybridized p orbitals to form \(\pi\) bonds.
3. Describe the bonding in HCN.

Solution:

A Because HCN is a linear molecule, it is likely that the bonding can be described in terms of sp hybridization at carbon. Because the nitrogen atom can also be described as sp hybridized, we can use one sp hybrid on each atom to form a C–N \(\sigma\) bond. This leaves one sp hybrid on each atom to either bond to hydrogen (C) or hold a lone pair of electrons (N). Of 10 valence electrons (5 from N, 4 from C, and 1 from H), 4 are used for \(\sigma\) bonding:

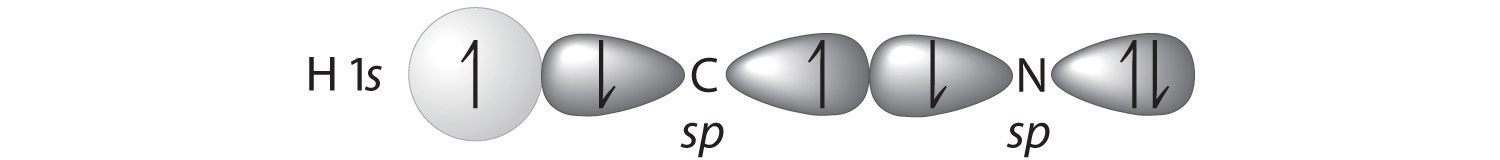
B We are now left with 2 electrons on N (5 valence electrons minus 1 bonding electron minus 2 electrons in the lone pair) and 2 electrons on C (4 valence electrons minus 2 bonding electrons). We have two unhybridized 2p atomic orbitals left on carbon and two on nitrogen, each occupied by a single electron. These four 2p atomic orbitals can be arranged in two pairs of parallel orbitals, yielding two \(\pi\) bonds.

C The overall result is a triple bond (1 \(\sigma\) and 2 \(\pi\)) between C and N.

Exercise

Describe the bonding in formaldehyde (H₂C=O), a trigonal planar molecule, using a combination of hybrid atomic orbitals and unhybridized orbitals.

Answer

• \(\sigma\)-bonding framework: Carbon and oxygen are sp² hybridized. Two sp² hybrid orbitals on oxygen have lone pairs, two sp² hybrid orbitals on carbon form C–H bonds, and one sp² hybrid orbital on C and O forms a C–O \(\sigma\) bond.
• \(\pi\) bonding: Unhybridized, singly occupied 2p atomic orbitals on carbon and oxygen interact to form a single \(\pi\) bond.

Once we have explored Molecular Orbital Theory we will revisit this description of multiple bonds to better understand the interactions of np orbitals to form \(\pi\) bonding type interactions.

Labeling Bonds in Valence Bond Theory

In VB Theory, we can describe each of the bonds within a molecule in terms of both the bond symmetry (\(\sigma\) or \(\pi\)) and the orbitals used to form the bond. Consider the bonding in ethylene (C₂H₄, Figure 4.7.1). The two carbon atoms are sp² hybridized, while the four hydrogen atoms' 1s orbitals remain unhybridized with a single electron in each 1s atomic orbital. The four \(\sigma\) bonds in ethylene can therefore be described as follows:

\(\sigma\) : C(sp²) - H(1s)

The double bond between the two carbon atoms is made up of one \(\sigma\) bond and one \(\pi\) bond. The \(\sigma\) bond results from overlapping sp² orbitals on the neighbouring carbon atoms. The single \(\pi\) bond is formed by overlap between parallel unhybridized 2p orbitals on the neighbouring carbon atoms. Thus, the double bond can be described as follows:

\(\sigma\) : C(sp²) - C(sp²)

\(\pi\) : C(2p) - C(2p)

Exercise

Label the bonds in formaldehyde (H₂C=O), in terms of the bond symmetry and the overlapping orbitals.

Answer

• The two carbon-hydrogen bonds are:
  \(\sigma\) : C(sp²) - H(1s)
• The carbon-oxygen double bond is:
  \(\sigma\) : C(sp²) - O(sp²)
  \(\pi\) : C(2p) - O(2p)

Summary

• Polyatomic systems with multiple bonds can be described using hybrid atomic orbitals for \(\sigma\) bonding and unhybridized np orbitals to describe \(\pi\) bonding.

To describe the bonding in more complex molecules with multiple bonds, we can use an approach that uses hybrid atomic orbitals to describe the \(\sigma\) bonding and unhybridized np orbitals to describe the \(\pi\) bonding. In this approach, parallel unhybridized np orbitals on atoms bonded to one another are allowed to interact to produce bonding.