Skip to main content
Chemistry LibreTexts

6.2: Mole Ratios

  1. Last updated
  2. Save as PDF
  • Page ID
    367791

    • Anonymous
    • LibreTexts
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Suppose that you want to add some sections to your porch. Before you go to the hardware store to buy lumber, you need to determine the unit composition (the material between two large uprights). You count how many posts, how many boards, how many rails—then you decide how many sections you want to add—before you calculate the amount of building material needed for your porch expansion.

    Mole Ratios

    Stoichiometry problems can be characterized by two things: (1) the information given in the problem, and (2) the information that is to be solved for, referred to as the unknown. The given and the unknown may both be reactants, both be products, or one may be a reactant while the other is a product. The amounts of the substances can be expressed in moles. However, in a laboratory situation, it is common to determine the amount of a substance by finding its mass in grams. The amount of a gaseous substance may be expressed by its volume. In this concept, we will focus on the type of problem where both the given and the unknown quantities are expressed in moles.

    CK12 Screenshot 12-2-1.png
    Figure \(\PageIndex{1}\): Mole ratio relationship.

    Chemical equations express the amounts of reactants and products in a reaction. The coefficients of a balanced equation can represent either the number of molecules or the number of moles of each substance. The production of ammonia \(\left( \ce{NH_3} \right)\) from nitrogen and hydrogen gases is an important industrial reaction called the Haber process, after German chemist Fritz Haber.

    \[\ce{N_2} \left( g \right) + 3 \ce{H_2} \left( g \right) \rightarrow 2 \ce{NH_3} \left( g \right)\]

    The balanced equation can be analyzed in several ways, as shown in the figure below.

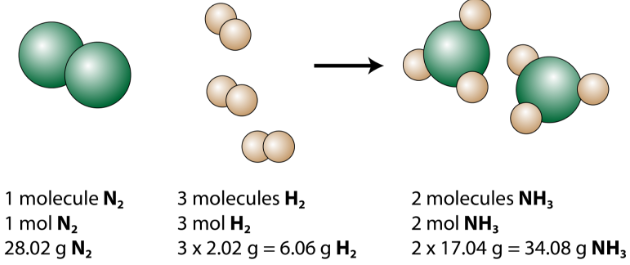
    CK12 Screenshot 12-2-2.png
    Figure \(\PageIndex{2}\): This representation of the production of ammonia from nitrogen and hydrogen shows several ways to interpret the quantitative information of a chemical reaction.

    We see that 1 molecule of nitrogen reacts with 3 molecules of hydrogen to form 2 molecules of ammonia. This is the smallest possible relative amount of the reactants and products. To consider larger relative amounts, each coefficient can be multiplied by the same number. For example, 10 molecules of nitrogen would react with 30 molecules of hydrogen to produce 20 molecules of ammonia.

    The most useful quantity for counting particles is the mole. So if each coefficient is multiplied by a mole, the balanced chemical equation tells us that 1 mole of nitrogen reacts with 3 moles of hydrogen to produce 2 moles of ammonia. This is the conventional way to interpret any balanced chemical equation.

    Finally, if each mole quantity is converted to grams by using the molar mass, we can see that the law of conservation of mass is followed. \(1 \: \ce{mol}\) of nitrogen has a mass of \(28.02 \: \text{g}\), while \(3 \: \text{mol}\) of hydrogen has a mass of \(6.06 \: \text{g}\), and \(2 \: \text{mol}\) of ammonia has a mass of \(34.08 \: \text{g}\).

    \[28.02 \: \text{g} \: \ce{N_2} + 6.06 \: \text{g} \: \ce{H_2} \rightarrow 34.08 \: \text{g} \: \ce{NH_3}\]

    Mass and the number of atoms must be conserved in any chemical reaction. The number of molecules is not necessarily conserved.

    CK12 Screenshot 12-2-3.png
    Figure \(\PageIndex{3}\): An apparatus for running the Haber process.

    A mole ratio is a conversion factor that relates the amounts in moles of any two substances in a chemical reaction. The numbers in a conversion factor come from the coefficients of the balanced chemical equation. The following six mole ratios can be written for the ammonia forming reaction above.

    \[\begin{array}{ccc} \dfrac{1 \: \text{mol} \: \ce{N_2}}{3 \: \text{mol} \: \ce{H_2}} & or & \dfrac{3 \: \text{mol} \: \ce{H_2}}{1 \: \text{mol} \: \ce{N_2}} \\ \dfrac{1 \: \text{mol} \: \ce{N_2}}{2 \: \text{mol} \: \ce{NH_3}} & or & \dfrac{2 \: \text{mol} \: \ce{NH_3}}{1 \: \text{mol} \: \ce{N_2}} \\ \dfrac{3 \: \text{mol} \: \ce{H_2}}{2 \: \text{mol} \: \ce{NH_3}} & or & \dfrac{2 \: \text{mol} \: \ce{NH_3}}{3 \: \text{mol} \: \ce{H_2}} \end{array}\]

    In a mole ratio problem, the given substance, expressed in moles, is written first. The appropriate conversion factor is chosen in order to convert from moles of the given substance to moles of the unknown.

    Example \(\PageIndex{1}\)

    How many moles of ammonia are produced if 4.20 moles of hydrogen are reacted with an excess of nitrogen?

    Solution

    Step 1: List the known quantities and plan the problem.

    Known

    4.20 moles of hydrogen

    relevant mole ratios from balanced equation.

    Unknown

    mol NH3

    Plan

    The conversion is from \(\text{mol} \: \ce{H_2}\) to \(\text{mol} \: \ce{NH_3}\). The problem states that there is an excess of nitrogen, so we do not need to be concerned with any mole ratio involving \(\ce{N_2}\). Choose the conversion factor that has the \(\ce{NH_3}\) in the numerator and the \(\ce{H_2}\) in the denominator.

    Step 2: Solve.

    \[4.20 \: \text{mol} \: \ce{H_2} \times \dfrac{2 \: \text{mol} \: \ce{NH_3}}{3 \: \text{mol} \: \ce{H_2}} = 2.80 \: \text{mol} \: \ce{NH_3}\]

    The reaction of \(4.20 \: \text{mol}\) of hydrogen with excess nitrogen produces \(2.80 \: \text{mol}\) of ammonia.

    Step 3: Think about your result.

    The result corresponds to the 3:2 ratio of hydrogen to ammonia from the balanced equation.

    Summary

    • Mole ratios allow comparison of the amounts of any two materials in a balanced equation.
    • Calculations can be made to predict how much product can be obtained from a given number of moles of reactant.

    This page titled 6.2: Mole Ratios is shared under a mixed license and was authored, remixed, and/or curated by Anonymous via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.