5.5: Predicting Reactions - Single and Double Replacement Reactions

Last updated
Save as PDF

Page ID: 367787

Anonymous
LibreTexts

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Learning Objectives

Predict the result of single-replacement reactions or double-replacement reactions.

Up until now, we have presented balancing and categorizing chemical reactions as topics, but we have not discussed how the products of a chemical reaction can be predicted. Here we will begin our study of certain types of chemical reactions that allow us to predict what the products of the reaction will be. In later chapters of this text, we will learn more about each of these reaction types related to predicting whether or not they will occur. For now, we will use the knowledge we have of predicting the formulas of ionic compounds and balancing equations to predict the results of certain reaction types, assuming the reactions will take place.

Predicting Single Replacement Reactions

A single-replacement reaction is a chemical reaction in which one element is substituted for another element in a compound, generating a new element and a new compound as products. Presented below:

\[\ce{2HCl(aq) + Zn(s) → ZnCl2(aq) + H2(g)}\nonumber \]

is an example of a single-replacement reaction. The hydrogen atoms in \(\ce{HCl}\) are replaced by \(\ce{Zn}\) atoms, and in the process a new element—hydrogen—is formed. Another example of a single-replacement reaction is

\[\ce{2NaCl(aq) + F2(g) → 2NaF(s) + Cl2(g)}\nonumber \]

Here the negatively charged ion changes from chloride to fluoride. A typical characteristic of a single-replacement reaction is that there is one element as a reactant and another element as a product.

Not all proposed single-replacement reactions will occur between two given reactants. In a later chapter, we will learn how to predict when certain single replacement reactions will occur. For now, we will focus on correctly predicting the result of single replacement reactions which involve ionic compounds. (If you would like to cover that material now, please refer to this other textbook, which has been adapted for the content in part of this section.)

If a single replacement reaction involves an ionic compound and an element, the element will replace an element in the ionic compound which it is most similar to. That is, a metal will replace a metal and a non-metal will replace a nonmetal. Use the periodic table to determine the typical charges of the anions and cations in the product. Whichever ion exists in a compound on both sides of the reaction will typically have the same charge in each case. Make sure to balance the charge of the new compound based on the expected charges of the ions involved.

Example \(\PageIndex{1}\):

Identify the products of the following single-replacement reactions?

FeCl₂ + Ca → ?
CaBr₂ + F₂ → ?

Solution

The products of this single-replacement reaction are CaCl₂ and Fe.
The products of the reaction will be CaF₂ and Br₂.

Exercise \(\PageIndex{1}\)

Identify the products of the following single-replacement reactions?

\[\ce{FeI2 + Cl2 → }\nonumber \]

Answer: Yes; FeCl₂ and I₂

Exercise \(\PageIndex{2}\)

Identify the products of the following single-replacement reactions?

\[\ce{AlPO4 + Mg → }\nonumber \]

Answer: Mg₃(PO₄)₂ and Al (Note the charge balance in the compound)

Predicting Double Replacement Reactions

Predicting whether a double-replacement reaction occurs is somewhat more difficult than predicting a single-replacement reaction. We will explore one type of double replacement reaction in a later chapter: the precipitation reaction. For now, the goal of correctly predicting the result of a precipitation reaction involves understanding how charge balances work in the two new species which form. Similar to the single replacement reaction, not all possible double replacement reactions will occur. However, for the sake of correctly predicting the charge balance of the products, we will only consider reactions which do occur for the rest of this chapter. (If you would like to cover that material now, please refer to this other textbook, which has been adapted for the content in the remainder of this section.)

When predicting the result of a double replacement reaction, it is important to go through the following 3 steps. (Please note: when we learn how to predict whether or not the reaction occurs, we will be adding a 4^th step as well.)

Change the partners of the anions and cations on the reactant side to form new compounds (products).
Correct the formulas of the products based on the charges of the ions.
Balance the equation.

For example, predict what will happen when aqueous solutions of barium chloride (BaCl₂) and lithium sulfate (Li₂SO₄) are mixed.

Change the partners of the anions and cations on the reactant side to form new compounds (products):

Chemical equation of the reactants barium chloride and lithium sulfate forming the products barium sulfate and lithium chloride.

Please note, that the only subscript which transfers across from reactant to product in this step is the 4 on the oxygen. This is because the oxygen is part of a polyatomic ion (sulfate). The subscripts of 2 on the lithium and chloride are not transferred here. These subscripts are not parts of the ion. Instead, they are telling us how many of that ion was necessary for the charge balance. If we need new subscripts, we will determine that in the next step.

Correct the formulas of the products based on the charges of the ions.

In this particular case, there is no need to make additional changes because the ions balance as shown. Let’s verify this by looking at the charges of all of the ions present: \(\ce{Ba^{2+}}\), \(\ce{Cl^{−}}\), \(\ce{Li^{+}}\), and \(\ce{SO4^{2−}}\). (note: if you are unsure how we determined these charges, please refer to the section of this book where we first discussed ionic compounds.) Because in each case the charges of the anion and cation canceled within each compound, there was no need to change any of the coefficients from the assumed value of one.

Balance the equation:

It is only once we have correctly predicted the formulas of the products that we can consider balancing the overall equation. In this case, we will look at the initial subscripts to determine what coefficients we might need for the products. Please note, that subscripts should have been determined in the previous step. If the equation still remains unbalanced we add coefficients as shown below.

\[\ce{BaCl_2(aq) + Li_2SO_4(aq) \rightarrow BaSO_4 + 2LiCl} \nonumber \]

Figure \(\PageIndex{2}\): An x-ray of the digestive organs of a patient who has swallowed a “barium milkshake.” A barium milkshake is a suspension of very fine BaSO₄ particles in water; the high atomic mass of barium makes it opaque to x-rays. (Public Domain; Glitzy queen00 via Wikipedia).

Example \(\PageIndex{1}\)

Predict what will happen if rubidium hydroxide and cobalt(II) chloride are mixed.

Solution

Steps

Example

Change the partners of the anions and cations on the reactant side to form new compounds (products).

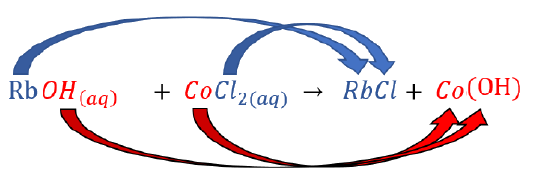Chemical equation of the reactants rubidium hydroxide and cobalt(II) chloride forming the products rubidium chloride and cobalt hydroxide.

Correct the formulas of the products based on the charges of the ions.

\(\ce{RbOH(aq) + CoCl2(aq) \rightarrow RbCl + Co(OH)_2}\)

Balance the equation.

Coefficients already balanced.

\(\ce{RbOH(aq) + CoCl_2(aq) \rightarrow RbCl(aq) + Co(OH)_2(s)}\)

Example \(\PageIndex{2}\)

Predict what will happen if aqueous solutions of strontium bromide and aluminum nitrate are mixed.

Solution

Steps	Example
Change the partners of the anions and cations on the reactant side to form new compounds (products).
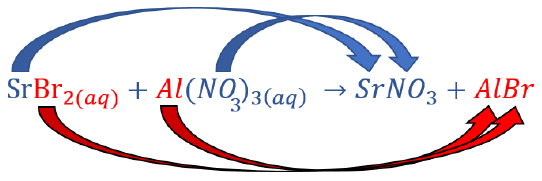Correct the formulas of the products based on the charges of the ions.	\(\ce{SrBr_2(aq) + Al(NO_3)_3(aq) \rightarrow Sr(NO_3)_2 + AlBr_3}\)
Balance the equation.	\(\ce{3 SrBr_2(aq) + 2 Al(NO_3)_3(aq) \rightarrow 3 Sr(NO_3)_2 + 2 AlBr_3}\)

As mentioned at the start of this discussion, we will be adding a 4^th step in order to determine whether these reactions will occur in a later chapter. In fact, we will revisit these same examples and decide if the reaction occurs or not. It turns out that one of them does, and one of them doesn’t. For now, assume any question about double replacement reactions you see in exercises are reactions which will occur. Your job will be to use the 3 steps we discussed to determine the final balanced equation.

Summary

We have learned how to predict the results of single replacement and double replacement reactions using only concepts of charge balance within a compound and balancing equations among compounds and elements. In later chapters we will learn other considerations for predicting both of these types of reactions.

Key Takeaways

A single-replacement reaction replaces one element for another in a compound.
A double-replacement reaction exchanges the cations (or the anions) of two ionic compounds.